在练习1至6中检查方程组的一致性。
问题1. x + 2y = 2
2x + 3y = 3
解决方案:
Matrix form of the given equations is AX = B
where, A =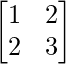 , B =
, B = ![]() and, X =
and, X = ![]()
∴ 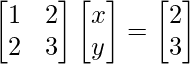
Now, |A| = 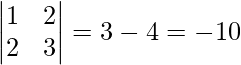
∵ Inverse of matrix exists, unique solution.
∴ System of equation is consistent.
问题2。2x– y = 5
x + y = 4
解决方案:
Matrix form of the given equations is AX = B
where, A =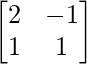 , B =
, B =![]() and, X =
and, X =![]()
∴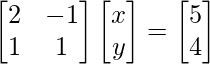
Now, |A| =
∵ Inverse of matrix exists, unique solution.
∴ System of equation is consistent.
问题3. x + 3y = 5
2x + 6y = 8
解决方案:
Matrix form of the given equations is AX = B
where, A = , B =
, B = ![]() and, X =
and, X =![]()
∴ 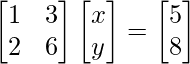
Now, |A| =
And, adj. A =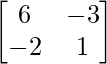
∴ (adj. A) B = 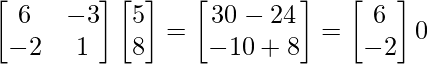
∵ Have no common solution.
∴ System of equation is inconsistent.
问题4. x + y + z = 1
2x + 3y + 2z = 2
斧头+ ay + 2az = 4
解决方案:
Matrix form of the given equations is AX = B
where, A =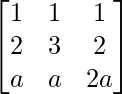 , B =
, B =![]() and, X =
and, X =![]()
∴ 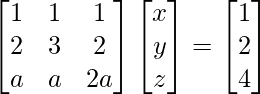
Now, |A| = 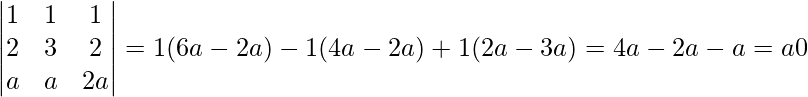
∵ Inverse of matrix exists, unique solution.
∴ System of equation is consistent.
问题5。3x – y – 2z = 2
2y – z = -1
3x – 5y = 3
解决方案:
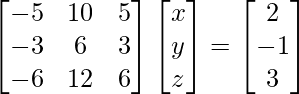
Matrix form of the given equations is AX = B
where, A =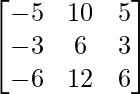 , B=
, B=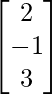 and, X =
and, X =![]()
∴
Now, |A| =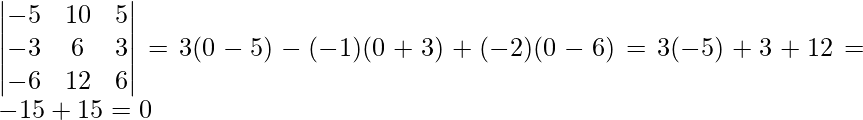
And, adj. A =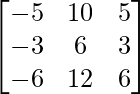
∴ (adj. A) B =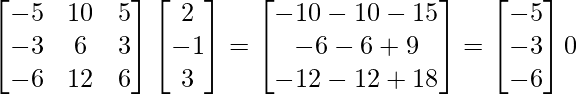
∴ System of equation is inconsistent.
问题6. 5x – y + 4z = 5
2x + 3y + 5z = 2
5x – 2y + 6z = –1
解决方案:
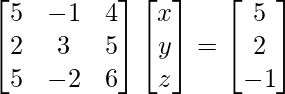
Matrix form of the given equations is AX = B
where, A =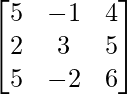 , B =
, B =  and, X=
and, X=![]()
∴
Now, |A| =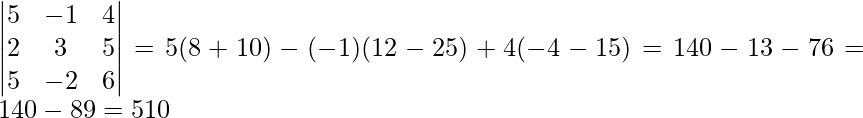
∵ Inverse of matrix exists, unique solution.
∴ System of equation is consistent.
在练习7至14中,使用矩阵方法求解线性方程组。
问题7. 5x + 2y = 4
7x + 3y = 5
解决方案:
Matrix form of the given equations is AX = B
where, A=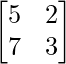 , B=
, B=![]() , X=
, X=![]()
∴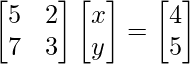
Now, |A|=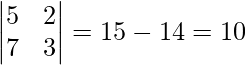
∴Unique solution
Now, X = A-1B =![]() (adj.A)B
(adj.A)B
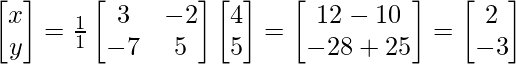
Therefore, x=2 and y=-3
问题8。2x – y = -2
3x + 4y = 3
解决方案:
Matrix form of the given equations is AX = B
where, A= , B=
, B= , X=
, X=![]()
∴
Now, |A|=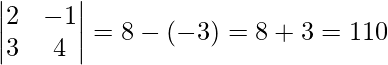
∴Unique solution
Now, X = A-1B ![]() (adj.A)B
(adj.A)B

Therefore, x=-5/11 and y=12/11
问题9. 4x – 3y = 3
3x – 5y = 7
解决方案:
Matrix form of the given equations is AX = B
where, A=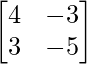 , B=
, B=![]() , X=
, X=![]()
∴
Now, |A|=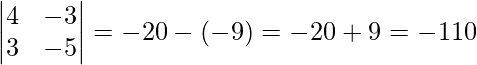
∴Unique solutio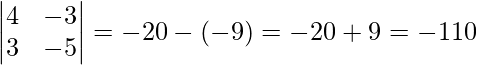 n
n
Now, X =A-1B ![]() A(adj.A)B
A(adj.A)B

Therefore, x= -6/11 and y= -19/11
问题10.5x + 2y = 3
3x + 2y = 5
解决方案:
Matrix form of the given equations is AX = B
where, A=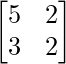 , B=
, B=![]() , X=
, X=![]()
∴
Now, |A|=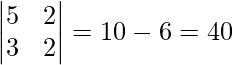
∴Unique solution
Now, X = A-1B![]() A(adj.A)B
A(adj.A)B
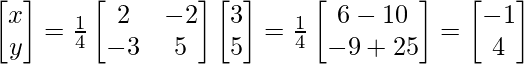
Therefore, x= -1 and y= 4