第12类NCERT解决方案–数学第I部分–第4章行列式–练习4.4

写下以下行列式元素的未成年人和辅助因子：

问题1

(一世) 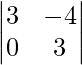$\begin{vmatrix}3&-4\\0&3\end{vmatrix}$

(ii) 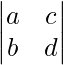$\begin{vmatrix}a&c\\b&d\end{vmatrix}$

解决方案：

(i) $\begin{vmatrix}3&-4\\0&3\end{vmatrix}$

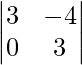
Finding minors of the elements of the determinant: 

Let us assume M_ij is Minors of elements a_ij

M₁₁ = Minor of elements a₁₁ = 3

M₁₂ = Minor of elements a₁₂ = 0

M₂₁ = Minor of elements a₂₁ = −4

M₂₂ = Minor of elements a₂₂ = 2

Finding cofactor of a_ij

Let us assume cofactor of a_ij is A_ij M_ij

A₁₁ = (−1)¹⁺¹ M₁₁ = (−1)² (3) = 3

A₁₂ = (−1)¹⁺² M₁₂ = (−1)³ (0) = 0

A₂₁ = (−1)²⁺¹ M₂₁ = (−1)³ (−4) = 4

A₂₂ = (−1)²⁺² M₂₂ = (−1)⁴ (2) = 2

(ii) 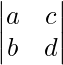$\begin{vmatrix}a&c\\b&d\end{vmatrix}$

Finding minors of the elements of the determinant:

Let us assume M_ij is Minors of elements a_ij

M₁₁ = Minor of element a₁₁ = d

M₁₂ = Minor of elements a₁₂ = b

M₂₁ = Minor of elements a₂₁ = c

M₂₂ = Minor of elements a₂₂ = a

Finding cofactor of a_ij

Let us assume cofactor of a_ij is A_ij, which is (−1)^i+j M_ij

A₁₁ = (−1)¹⁺¹ M₁₁ = (−1)² (d) = d

A₁₂ = (−1)¹⁺² M₁₂ = (−1)³ (b) = −b

A₂₁ = (−1)²⁺¹ M₂₁ = (−1)³ (c) = −c

A₂₂ = (−1)²⁺² M₂₂ = (−1)⁴ (a) = a

问题2。

(一世) $\begin{vmatrix}1&0&0\\0&1&0\\0&0&1\end{vmatrix}$

(ii) $\begin{vmatrix}1&0&4\\3&5&-5\\0&2&2\end{vmatrix}$

解决方案：

(i) $\begin{vmatrix}1&0&0\\0&1&0\\0&0&1\end{vmatrix}$

Let us find the Minors and cofactors of the elements:

Assume, M_ij is minor of element a_ij and A_ij is cofactor of a_ij

M₁₁ = Minor of elements a₁₁ =$\begin{vmatrix} 1 & 0\\0 & 1\end{vmatrix}$= 1 − 0 = 1 and A₁₁ = 1

M₁₂ = Minor of elements a₁₂ =$\begin{vmatrix} 0 & 0\\0 & 1\end{vmatrix}$= 0 − 0 = 0 and A₁₂ = 0

M₁₃ = Minor of elements a₁₃ =$\begin{vmatrix} 0 & 1\\0 & 0\end{vmatrix}$= 0 − 0 = 0 and A₁₃ = 0

M₂₁ = Minor of elements a₂₁ =$\begin{vmatrix} 0 & 0\\0 & 1\end{vmatrix}$= 0 − 0 = 0 and A₂₁ = 0

M₂₂ = Minor of elements a₂₂ =$\begin{vmatrix} 1 & 0\\0 & 1\end{vmatrix}$= 1 − 0 = 1 and A₂₂ = 1

M₂₃ = Minor of elements a₂₃ =$\begin{vmatrix} 1 & 0\\0 & 0\end{vmatrix}$= 0 − 0 = 0 and A₂₃ = 0

M₃₁ = Minor of elements a₃₁ =$\begin{vmatrix} 0 & 0\\1 & 0\end{vmatrix}$= 0 − 0 = 0 and A₃₁ = 0

M₃₂ = Minor of elements a₃₂ =$\begin{vmatrix} 1 & 0\\0 & 0\end{vmatrix}$= 0 − 0 = 0 and A₃₂ = 0

M₃₃ = Minor of elements a₃₃ =$\begin{vmatrix} 1 & 0\\0 & 1\end{vmatrix}$= 1 − 0 = 1 and A₃₃ = 1

(ii) 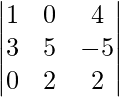$\begin{vmatrix}1&0&4\\3&5&-5\\0&2&2\end{vmatrix}$

Let us find the Minors and cofactors of the elements:

Assume, M_ij is minor of element a_ij and A_ij is cofactor of a_ij

M₁₁ = Minor of elements a₁₁ =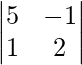$\begin{vmatrix} 5 & -1\\1 & 2\end{vmatrix}$= 10 − (−1) = 11 and A₁₁ = 11

M₁₂ = Minor of elements a₁₂ =$\begin{vmatrix} 3 & -1\\0 & 2\end{vmatrix}$= 6 − 0 = 6 and A₁₂ = −6

M₁₃ = Minor of elements a₁₃ =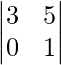$\begin{vmatrix} 3 & 5\\0 & 1\end{vmatrix}$= 3 − 0 = 3 and A₁₃ = 3

M₂₁ = Minor of elements a₂₁ =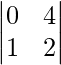$\begin{vmatrix} 0 & 4\\1 & 2\end{vmatrix}$= 0 − 4 = −4 and A₂₁ = 4

M₂₂ = Minor of elements a₂₂ =$\begin{vmatrix} 1 & 4\\0 & 2\end{vmatrix}$= 2 − 0 = 2 and A₂₂ = 2

M₂₃ = Minor of elements a₂₃ =$\begin{vmatrix} 1 & 0\\0 & 1\end{vmatrix}$= 1 − 0 = 1 and A₂₃ = −1

M₃₁ = Minor of elements a₃₁ =$\begin{vmatrix} 0 & 4\\5 & -1\end{vmatrix}$= 0 − 20 = −20 and A₃₁ = −20

M₃₂ = Minor of elements a₃₂ =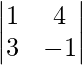$\begin{vmatrix} 1 & 4\\3 & -1\end{vmatrix}$= −1 − 12 = −13 and A₃₂ = 13

M₃₃ = Minor of elements a₃₃ =$\begin{vmatrix} 1 & 0\\3 & 5\end{vmatrix}$= 5 − 0 = 5 and A₃₃ = 5

问题3.使用第二行元素的辅因子，评估△?

$\bigtriangleup=\begin{vmatrix}5&3&8\\2&0&1\\1&2&3\end{vmatrix}$

解决方案：

Finding the Cofactors of elements of second row:

A₂₁ = Cofactor of elements a₂₁ = (−1)²⁺¹  $\begin{vmatrix} 3 & 8\\2 & 3\end{vmatrix}$= (−1)³ (9 − 16) = 7

A₂₂ = Cofactor of elements a₂₂ = (−1)²⁺² 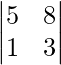 $\begin{vmatrix} 5 & 8\\1 & 3\end{vmatrix}$= (−1)⁴ (15 − 8) = 7

A₂₃ = Cofactor of elements a₂₃ = (−1)²⁺³ 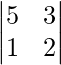 $\begin{vmatrix} 5 & 3\\1 & 2\end{vmatrix}$= (−1)⁵ (10 − 3) = 7

Now, △ = a₂₁ A₂₁ + a₂₂ A₂₂ + a₂₃ A₂₃ = 14 + 0 − 7 = 7

问题4.使用第三列元素的辅因子评估△?

$\bigtriangleup = \begin{vmatrix}1&x&yz\\1&y&zx\\1&z&xy\end{vmatrix}$

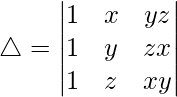
解决方案：

Finding the Cofactors of elements of third column:

A₁₃ = Cofactor of elements a₁₃ = (−1)¹⁺³  $\begin{vmatrix} 1 & y\\1 & z\end{vmatrix}$= (−1)⁴ (z − y) = −y

A₂₃ = Cofactor of elements a₂₃ = (−1)²⁺³ 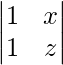 $\begin{vmatrix} 1 & x\\1 & z\end{vmatrix}$= (−1)⁵ (z − x) = x − z

A₃₃ = Cofactor of elements a₃₃ = (−1)³⁺³ 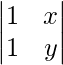 $\begin{vmatrix} 1 & x\\1 & y\end{vmatrix}$= (−1)⁶ (y − x) = y − x

Now, △ = a₁₃ A₁₃ + a₂₃ A₂₃ + a₃₃ A₃₃

= yz (z − y) + zx (x − z) + xy (y − x)

= (yz² − y²z) + (xy² − xz²) + (xz² − x²y)

= (y − z)[−yz + x(y + z) − x²]

= (y − z)[−yz + x (z − x) + x (z − x)]

= (x − y)(y − x)(z − x)

问题5。 $△=\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}$和A _ij是一个_IJ然后△的值由下式给出的辅因子：

(A)一个₁₁ A ₃₁ +一个₁₂ A ₃₂ +一个₁₃ A ₃₃

(B) ₁₁ A ₁₁ + ₁₂ A ₂₁ + ₁₃ A ₃₁

(C) ₂₁ A ₁₁ + ₂₂ A ₁₂ + ₂₃ A ₁₃

(D)一个₁₁ A ₁₁ +一个₂₁ A ₂₁ +一个₃₁ A ₃₁

解决方案：

Option (D) is correct.