三角函数的反导| 12年级数学

从最简单到最复杂的每个数学函数都有一个逆函数。在数学中，逆通常表示相反的意思。另外，逆是减法。对于乘法，它是除法。与三角函数相同，它是反三角函数。三角函数是角度的函数。术语函数用于描述两组数字或变量之间的关系。在现代数学中，有六个基本的三角函数：正弦，余弦，正切，割线，正割和余切。这些函数的反函数是反正弦，反余弦，反正切，反正割，反正割和反正切。三角函数是多对一的函数，但我们知道，如果函数是双射(一一对应到)一个函数的反函数存在。因此，如果我们限制三角函数的域，则这些函数将变成双射的，并且三角函数的逆函数将在限制域内定义。

Note: Inverse of f is denoted by ” f ^-1 “.

反三角函数的域和范围

X的元素称为f的域，Y的元素称为f的域。 X元素的图像称为范围，它是Y的子集。下图演示了函数的域，共域和范围。

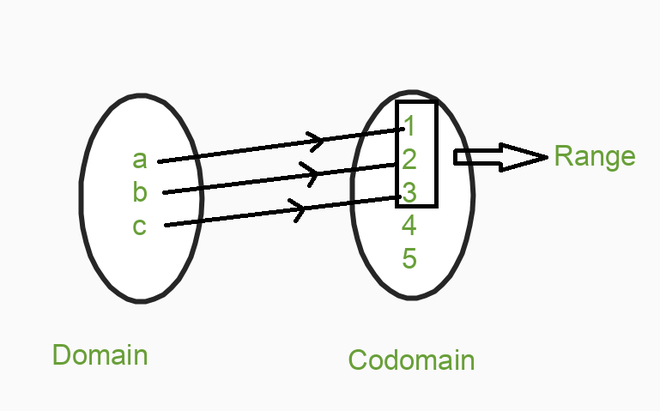
以下是反三角函数的域和范围的表：

Function	Domain	Range
sin-1x	[-1, 1]	[ -pi/2, pi/2 ]
cos-1x	[-1, 1]	[0, pi]
tan-1x	R	[-pi/2, pi/2]
cot-1x	R	(0, pi)
sec-1x	R-(-1,1)	[0, pi], {pi/2}
cosec-1x	R-(-1,1)	[ -pi/2, pi/2 ] – {0}

使用第一原理的反三角函数的导数

让我们通过解决一些问题来理解该主题，我们将使用“第一主体”解决这些问题。

问题陈述：在给定条件-1≤x≤1时，sin ^-1 x = y，-pi / 2≤y≤pi / 2。通过使用第一负责人来解决此问题。

Solution: 

Firstly taking sin on both sides, hence we get x = siny this equation is nothing but a function of y. Instead of finding dy/dx we will find dx/dy, so by definition of derivative we can write ((f(y + h) – f(y))/h), where h -> 0 under the limiting condition (see fourth line). Now replace the function with ((sin(y + h) – siny)/h) where h -> 0 under the limiting condition. Using the identity we can solve further. As we see in the last line of the below solution that siny and cosy are not dependent on the limit h -> 0 that’s why we had taken them out.

sin(sin x) = sin y

x = sin y

By definition of derivative,

dx/dy = lim_h->0 {f(y + h) – f(y)} / h

= lim_h->0 { sin(y + h) – siny } / h

Using identity: sin(A + B) = sinA.cosB + cosA.sinB, we can write,

= lim_h->0 (sin y . cos h + cos y . sin h – sin y) / h

= lim_h->0 (sin y . cos h – sin y + cos y . sin h) / h

= lim_h->0 {sin y(cos h – 1) / h} + {cos y . sin h) / h}

= sin y. lim_h->0 {(cos h – 1) / h} + cos y. lim_h->0 {sin h / h}

Now, we had taken -1 common from the expression (cos h-1) and we get (see in 1st line of below figure). Now using the formula as written in line 2 of the below figure we can write our expression dx/dy = cos y, if we reciprocal this term we get dy/dx = 1/cos y this. We know that sin² x + cos² x = 1, by simplifying this formula to get our answer, we simplified it till the 6th line of the below figure. 

But how had we written the final answer to this problem?

Since -pi/2 ≤ sin^-1x ≤ pi/2. Hence -pi/2 ≤ y ≤ pi/2, we had written y in place of sin^-1x, look at above figure second line we had written x = siny, if we write this for y we can write this like y = sin^-1x this, that’s why we had written y in place of sin^-1x. This implies 0 ≤ cosy ≤ 1 because y is an angle which lies first and fourth quadrant only, but one thing to note here, since cosy is in the denominator of dy/dx hence it cannot be zero, 

Now we remove the equality 0 < cos y ≤ 1 by this inequality we can clearly say that cosy is a positive property, hence we can remove -ve sign from the second last line of the below figure. So, this implies dy/dx = 1 over the quantity square root of (1 – x²), which is our required answer.

Note: In the solution after removing square we are getting square-root on another side and with square-root +ve and – ve both signs take place which is denoted by +-squareroot in the solution.

= sin y. lim_h->0 { (cos h – 1) / h } + cos y. lim_h->0 { sin h / h }

By using the formula: lim_h->0 (1 – cos h) / h = 0 and lim_h->0 sin h / h = 1, we can write,

dx / dy = cos y

dy / dx = 1 / cos y …..(1)

We know that sin²y + cos²y = 1, so cos²y = 1 – sin²y

⇒ cos = +- √(1 – sin²y), taking siny = x

we get, cosy = +-√(1 – x²)

dy / dx = 1 / √(1 – x²)

如果绘制正弦x的正弦图，则该图看起来像这样：

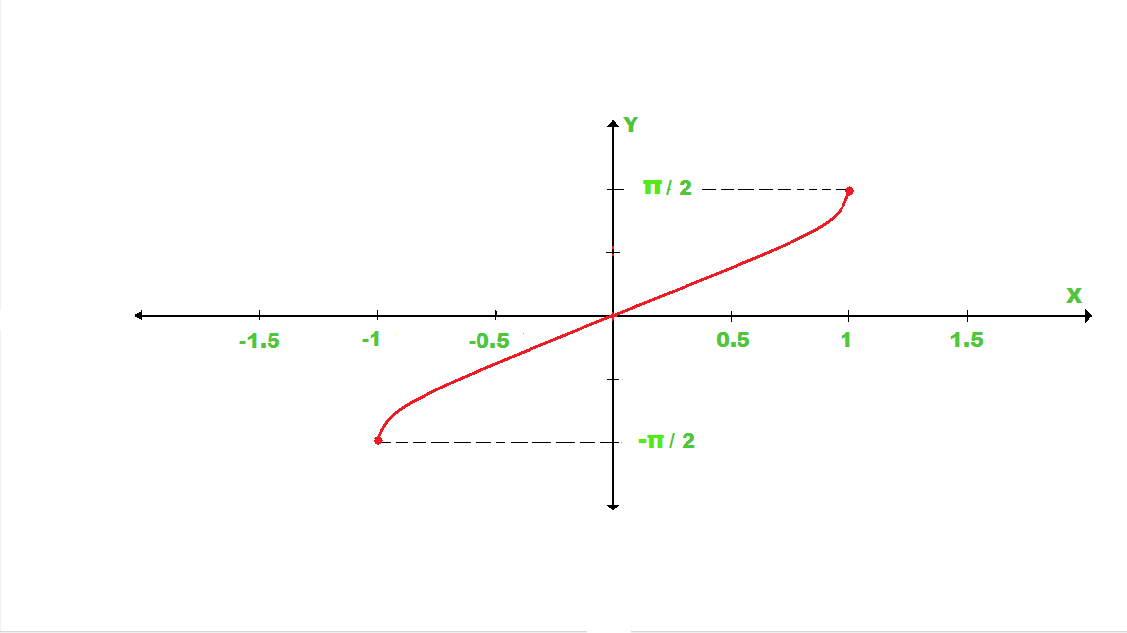
例子

示例1：使用第一原理微分函数f (x)= cos ^-1 x。

Solution: 

For solving and finding the cos^-1x ,we have to remember below three listed formulae.

• lim_h->0 {f(x + h) – f(x)} / h
• cos^-1x + sin^-1x = pi/2
• cos^-1x = pi/2 – sin^-1x

Now, let’s solve, we have.

f(x) = cos^-1x

f(x + h) = cos^-1(x + h)

lim_h->0 {cos^-1(x + h ) – cos^-1(x)} / h

lim_h->0 {pi/2 – sin^-1(x + h) – (pi/2 – sin^-1x) } / h

lim_h->0 {pi/2 – sin^-1(x + h) – pi/2 + sin^-1x } / h

Taking – sign common, we get

– lim_h->0 {sin^-1(x + h) – sin^-1x} / h

Since we know that lim_h->0 { sin^-1(x + h) – sin^-1x } / h = 1 / √(1 – x²)

Putting the value in our solution we get,

– 1 / √(1 – x²)

如果我们绘制cos逆x的图，则该图看起来像这样。

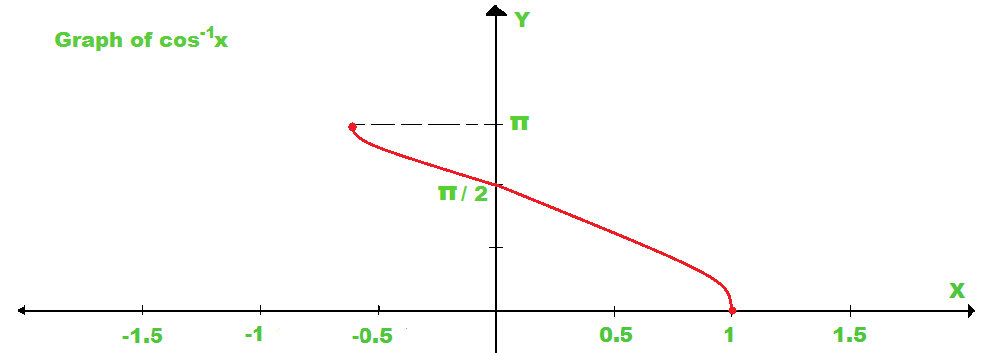
示例2：使用第一原理求解f(x)= tan ^-1 (x)。

Solution: 

For solving and finding tan^-1x, we have to remember some formulae, listed below.

• lim_h->0 {f(x + h) – f(x)} / h
• tan^-1(θ/θ) = 1
• tan^-1x – tan^-1y = tan^-1[(x – y) / (1 + xy)]

f(x) = tan^-1x

f(x + h) = tan^-1(x + h)

Apply 1st formula

lim_h->0 {tan^-1(x + h) – tan^-1x } / h

Now Apply 3rd formula

lim_h->0 tan^-1[(x – h – x) / (1 + (x + h)x] / h

lim_h->0 tan^-1[(h  / (1 + x² + xh ] / h . [(1 + x² + xh) / (1 + x² + xh)]

lim_h->0 tan^-1 {h / 1 + x² + xh} / {h / 1 + x² + xh} . lim_h->0 1 / 1 + x² + xh

Now we made the solution like so that we apply the 2nd formula

= 1 . 1 / (1 + x² + x . 0)

= 1 / (1 + x²)

如果我们绘制tan逆x的图，则该图看起来像这样。

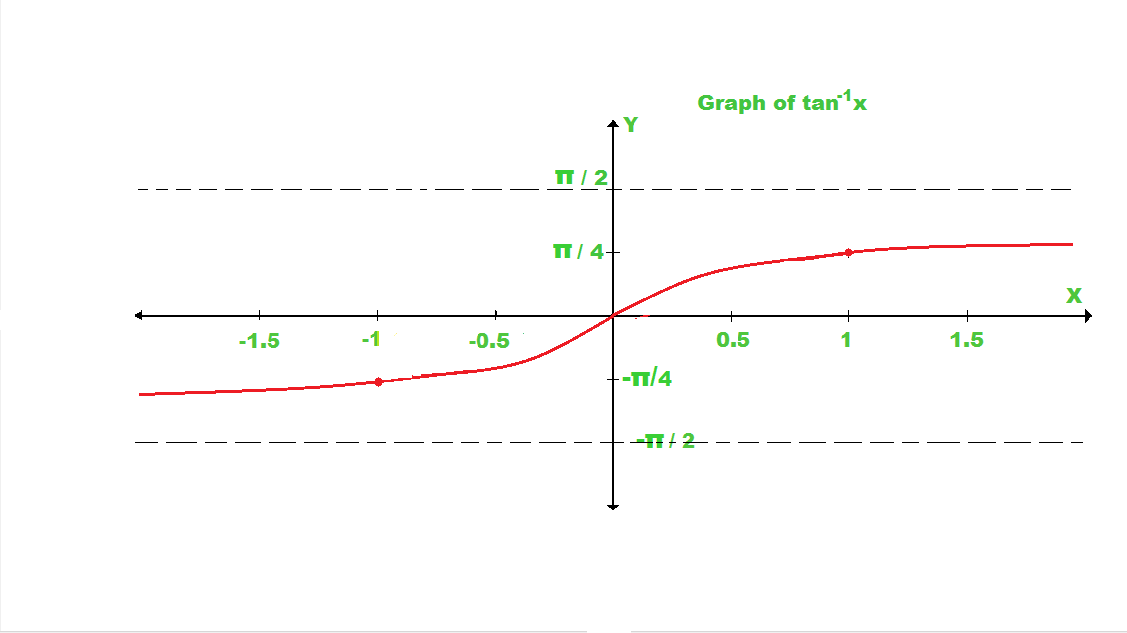
使用链规则的反三角函数导数

在使用链式规则之前，我们必须首先知道什么是链式规则?

uv = u’v + uv’

上面的表达式演示了链式规则，其中u是第一个函数，v是第二个函数，要应用链式规则，我们必须首先取u的导数，然后在其他段上与v相乘，我们必须取u的导数v，然后将其乘以u，然后将两者相加。我们使用这种链式法则找到函数的导数。

反三角函数的公式

下图中有反三角函数公式的列表，在求解反三角函数的导数时，我们将使用它们来解决问题。

$1. \ { \frac{d}{dx}(sin^{-1}x) = \frac{1}{\sqrt{1 - x^2}}} \\ 2. \ { \frac{d}{dx}(cos^{-1}x) = \frac{-1}{\sqrt{1 - x^2}}} \\ 3. \ { \frac{d}{dx}(tan^{-1}x) = \frac{1}{1 + x^2}} \\ 4. \ { \frac{d}{dx}(cosec^{-1}x) = \frac{-1}{mod(x).\sqrt{x^2 - 1}}} \\ 5. \ { \frac{d}{dx}(sec^{-1}x) = \frac{1}{mod(x).\sqrt{x^2 - 1}}} \\ 6. \ { \frac{d}{dx}(cot^{-1}x) = \frac{-1}{1 + x^2}}$

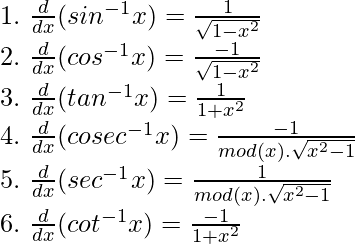
例子

让我们根据链式规则来解决一些问题，以正确理解此概念。

Note: In the all below Solutions y’ means dy/dx

问题1：y = tan ^-1 (1 / x)

Solution :

We have to find out the derivative of the above question, so first, we have to substitute the formulae of tan^-1x as we discuss in the above list (line 3). Then, we have to apply the chain rule. Then put the value of x in that formulae which are (1/x) then by applying the chain rule we have solved the question by taking there derivatives.

By using chain rule,

y’ = (tan^-1x)’

= {1/1 + (1/x²) } . (-1/x²)

= – x² / (x² + 1) . x²

问题2：y = sin ^-1 (1 – x)

Solution: 

We have to find out the derivative of the above question, so first, we have to substitute the formulae of tan^-1x as we discuss in the above list (line 1). Then, we have to apply the chain rule. Then put the value of x in that formulae which are (1 – x) then by applying the chain rule, we have solved the question by taking their derivatives.

By using chain rule,

y’ = (sin^-1(1 – x))’

= 1 / 1 – (x – 1)²

= 1 / √(1 – (x² – 2x + 1))

= 1 / √(2x – x²)

问题3：y =(1 / a)棕褐色^-1 (x / a)

Solution:

As we had solved the first problem in the same way we are going to solve this problem too, we have to find out the derivative of the above question, so first, we have to substitute the formulae of tan^-1x as we discuss in the above list (line 3). Then apply the chain rule. As we see 1/a is constant, so we take it out and applying the chain rule in tan^-1(x/a). Solved it by taking the derivative after applying chain rule.

By using chain rule,

y’ = ((1 / a) tan^-1(x / a))’

= (1 / a) {1 / (1 + (x / a))} . (x / a)’

= 1 / a . {1 / (1+ (x² / a²))} . (1 / a)

= 1 / a² . {a / (a² + x2)}

= a / a² + x²

问题4：y = cot ^-1 (1 / x ² )

Solution:

As we are solving the above three problem in the same way this problem will solve

By using chain rule,

y’ = (cot^-1(1 / x²))’

= { – 1 / (1 + (1 / x²))² } . (1 / x²)’

= { – 1 / (1 + (1 / x⁴)) . (-2x^-3)

= 2x⁴ / (x⁴ + 1)x³

= 2x / (1 + x⁴)

我们必须找出cot ^-1 (1 / x ² )的导数，因此首先我们必须在上面的三角公式列表(第4行)中替换cot ^-1 x的公式。然后应用链式规则，找到问题的导数，并在解决之后，我们得到我们需要的答案。

函数为隐函数微分学

首先，我们必须了解隐式函数。什么是隐式函数?让我们以一个函数为例，y = 2x +3。因此在此函数，变量y取决于变量x，这意味着x的值在y的函数值中更改时也会更改。因此，其中因变量(y)是孤立变量的这种类型的函数单独出现在一侧(左侧)，这些函数不是隐式函数，它们是显式函数。

让我们再举一个例子，x + sin xy -y =0。正如我们在该函数看到的那样，我们不能在一侧单独分离任何变量，这意味着我们不能隔离任何变量，因为我们同时拥有变量x和y罪恶的角度。因此，我们无法隔离变量的这种类型的函数。这种类型的函数称为隐式函数。让我们来解决这个问题，并通过使用隐式微分来解决该问题。

示例：y = cos ^-1 x

Solution: 

For finding derivative of of Inverse Trigonometric Function using Implicit differentiation. To start solving firstly we have to take the derivative x in both the sides, the derivative of cos(y) w.r.t x is -sin(y)y’. The reciprocal of sin is cosec so we can write in place of -1/sin(y) is -cosec(y) (see at line 7 in the below figure). Now we have to write the answer in terms of x, from equation(1) we draw the triangle for cos(y) = x and find the perpendicular of the triangle. Now the formula of cosec is hyp/perpendicular, now with the help of the triangle that we had drawn, we can find the cosec(y) by putting it in the formula. Then put the value of cosec(y) in the eq(2). We get our required answer(see the last line).

y = cos^-1x

y’ = (cos x)’

we can write,

cos y = x  …(1)

d/dx (cos y) = d/dx (x)

(-sin y) y’ = 1 / siny

y’ = -cosec y  …(2)

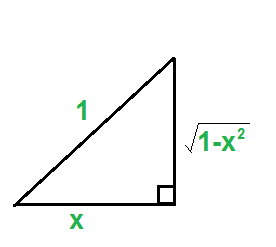
from eq (1), formula of cos(x) = base / hyp , we can find the perpendicular of triangle

perpendicular = √(1 – x²)

formula of cosec(x) = hyp / perpendicular, which is,

= 1 / √(1 – x²)

Putting the value of cosec in eq(2), we get

y’ = -1 / √(1 – x²)