问题1.如果P,Q和R是三个共线点,使得 和
和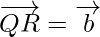 。找出向量
。找出向量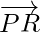
解决方案:
According to the question, given that
Points P, Q, and R are collinear.
Also, ![]() and
and ![]()
So,
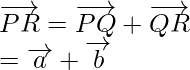
![]()
问题2.给定条件,三个向量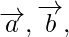 和
和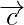 形成一个三角形的三个边。还有其他可能性吗?
形成一个三角形的三个边。还有其他可能性吗?
解决方案:
According to the question, given that ![]() are three sides of a triangle ABC.
are three sides of a triangle ABC.
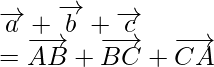
![]() [since
[since ![]() ]
]
![]() [since
[since ![]() ]
]
So, ![]()
As we know that if vectors are represented in magnitude and direction by the two sides
of triangle taken is same order, then their sum is represented by the third side taken in reverse order.
So,
![]()
or
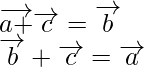
问题3。 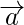 和
和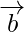 是具有相同初始点的两个非共线向量。代表的向量是什么
是具有相同初始点的两个非共线向量。代表的向量是什么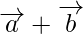 和
和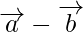 ?
?
解决方案:
According to the question, given that ![]() and
and ![]()
are two non-collinear vectors having the same initial point.
So, let us considered ![]()
Now we draw a parallelogram named as ABCD
Using the properties of parallelogram, we get
![]()
In ∆ABC,
Using the triangle law, we get
![]()
![]() …….(i)
…….(i)
In ∆ABD,
Using the triangle law, we get
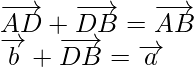
![]() …….(ii)
…….(ii)
On solving equation (i) and (ii), we get
![]() and
and ![]()
are diagonals of a parallelogram whose adjacent sides are ![]() and
and ![]()
问题4。 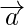 是一个向量,m是一个标量,使得
是一个向量,m是一个标量,使得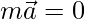 ,那么m和
,那么m和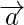 ?
?
解决方案:
According to the question, given that m is a scalar and ![]() is a vector such that
is a vector such that
![]()
![]() [since let
[since let ![]() ]
]
![]()
Now on comparing the coefficients of ![]() of LHS and RHS, we get
of LHS and RHS, we get
ma1 = 0 ⇒ m = 0 or a1 = 0 …….(i)
mb1 = 0 ⇒ m = 0 or b1 = 0 …….(ii)
mc1 = 0 ⇒ m = 0 or c1 = 0 …….(iii)
Now from eq (i), (ii) and (iii), we get
m = 0 or a1 = b1 = c1 = 0
m = 0 or ![]()
m = 0 or ![]()
问题5。 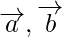 是两个向量,然后写以下语句的真值:
是两个向量,然后写以下语句的真值:
(一世) 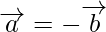 ⇒
⇒ 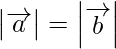
(ii) 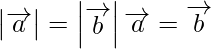
(iii) 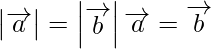
解决方案:
(i) Let us assume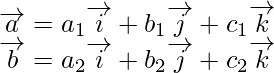
Given that, a = -b
So,
![]()
Now on comparing the coefficients of i, j, k in LHS and RHS, we get
a1 = a2 …….(i)
b1 = b2 …….(ii)
c1 = c2 …….(iii)
![]()
From eq(i), (ii), and (iii),
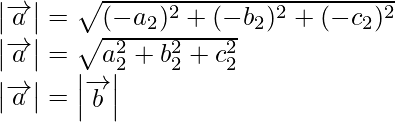
(ii) Given a and b are two vectors such that![]()
So, it means the magnitude of vector ![]() is equal to the magnitude
is equal to the magnitude
of vector ![]() , but we cannot find the direction of the vector.
, but we cannot find the direction of the vector.
Hence, it is false that
![]()
(iii) Given for any vector![]()
are equal but we cannot find the direction of the vector of ![]()
So, it is false.
问题6. ABCD是一个四边形。求向量之和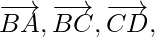 和
和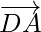 。
。
解决方案:
According to the question,
ABCD is a quadrilateral.
so,
In ∆ADC,
By using triangle law, we get
![]() ……(i)
……(i)
In ∆ABC,
By using triangle law, we get
![]() ……(ii)
……(ii)
Now put the value of ![]() in equation (ii), we get
in equation (ii), we get
![]()
Now on adding![]() on both sides,
on both sides,
![]()
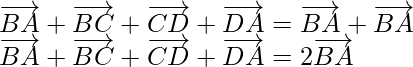
问题7:ABCDE是五边形,证明
(一世) 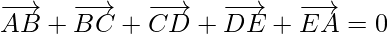
(ii) 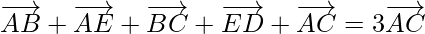
解决方案:
(i) According to the question,
ABCDE is a pentagon,
So,
![]()
Using the law of triangle ![]() , we get
, we get
![]()
![]()
![]()
Using triangle law ,![]() , we get
, we get
![]()
![]()
= 0
![]()
Hence Proved
(ii) According to the question,
ABCDE is a pentagon,
So,
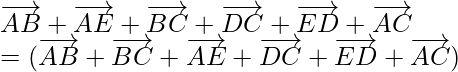
![]()
Using triangle law,![]() , we get
, we get
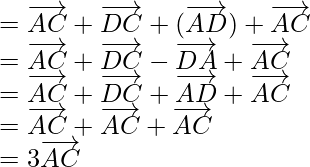
Hence Proved
问题8.证明从正八边形的中心到其顶点绘制的所有向量的总和为零向量。
解决方案:
Let us assume O be the centre of a regular octagon, as we know that the
centre of a regular octagon bisects all the diagonals passing through it.
So,
![]() …….(i)
…….(i)
![]() …….(ii)
…….(ii)
![]() …….(iii)
…….(iii)
![]() [Tex]\overrightarrow{OD}=-\overrightarrow{OH} [/Tex] …….(iv)
[Tex]\overrightarrow{OD}=-\overrightarrow{OH} [/Tex] …….(iv)
Now on adding equation (i), (ii), and (iv), we get
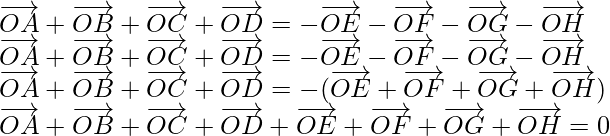
Hence proved
问题9:如果P是一个点,ABCD是四边形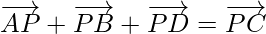 并且表明ABCD是平行四边形。
并且表明ABCD是平行四边形。
解决方案:
According to the question
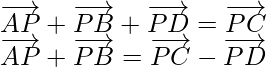
![]()
Since, ![]()
![]()
By using triangle law in ∆APB, ![]()
and using triangle law in ∆ DPC, ![]()
We get
![]()
So, AB is parallel to DC and equal is magnitude.
Hence, ABCD is a parallelogram.
问题10.五种力量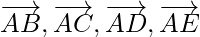 和
和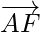 作用于正六边形ABCDEF的顶点。证明结果是6
作用于正六边形ABCDEF的顶点。证明结果是6 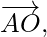 其中o是六边形的中心。
其中o是六边形的中心。
解决方案:
According to the question,
Prove that
![]()
Proof:
As we know that the centre(O) of the hexagon bisects the diagonal ![]()
So,
![]()
Now,
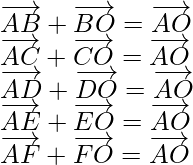
On adding these equations, we get
![]()
⇒![]()
But ![]()
So,
![]()
Hence proved