函数的可微性| 12年级数学

连续性或连续性，表示“如果函数的图形是没有断点或跳变的曲线，则函数在其域中是连续的” 。如果函数的图形在该点的紧邻范围内没有中断或跳跃，则该函数在其域中的某个点处将是连续的。

连续性：

A function f(x) is said to be continuous at a point x = a of its domain, if

(LHL) = (RHL) = f(a) or lim f(x) = f(a)

where 

(LHL)_{x = a}  = lim_{x -> a^–} f(x) and  

(RHL)_{x = a} = lim_{x -> a⁺} f(x)

Note: To evaluate LHL and RHL of a function f(x) at x = a, put x – h and x + h respectively, where h -> 0

一个点的不连续性：

If f(x) is not continuous at a point x = a, then it is discontinuous at x = a. 

有多种类型的不连续性：

• 可移动的不连续性：如果lim _{x-> a ^–} f(x)= lim _{x-> a ⁺} f(x)≠f(a)
• 第一种不连续性：如果lim _{x-> a ⁺} f(x)≠lim _{x-> a ⁺} f(x)
• 第二种不连续性：如果lim _{x-> a ^–} f(x)或lim _{x-> a ⁺} f(x)都不存在

可微性和可微性概念

A function f(x) is said to be differentiable at a point x = a, If Left hand derivative at (x = a) equals to Right hand derivative at (x = a) i.e 

LHD at(x = a) = RHD at (x = a),

where

Right hand derivative, Rf’ (a) = lim_h->0 (f(a + h) – f(a)) / h and

Left hand derivative Lf’ (a) = lim_h->0 (f(a – h) – f(a)) / -h

Note: The common value of Rf’ (a) and Lf’ (a)  is denoted by f'(a) and it is known as the derivative of f(x) at x = a. Every differentiable function is continuous but every continuous function need not be differentiable.

可微性的条件

条件1：该函数在该点上应该是连续的。如下图所示。

像这样

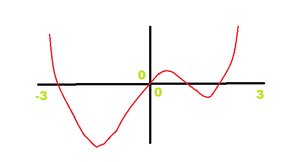
没有这个

条件2：图形在如下所示的点处没有尖角。

没有尖角

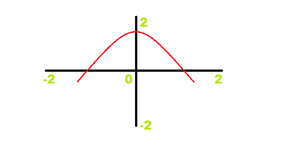
拥有锐利的曲线

条件3：图形在该点处没有垂直线。该图没有垂直线，如下图所示(由圆圈表示)。

指示图中的垂直线

Note: The relationship between continuity and differentiability is that all differentiable functions happen to be continuous but not all continuous functions can be said to be differentiable. Let’s discuss Differentiability and Continuity.

特殊功能的可微性

让我们考虑一些特殊功能：

1. f(x)= [x] ，它是x的最大整数，另一个是
2. f(x)= {x} ，它是x的小数部分

1.对于f(x)= [x]

因此，首先，我们使用f(x)= [x]来检查函数的微分性，我们必须首先绘制图形。所以我们来画图

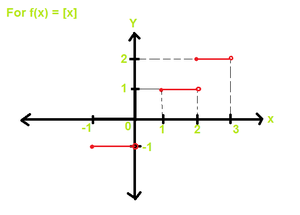
因此，正如我们在图中看到的那样，在0和1之间，函数的值是0，在1和2之间，函数的值是1，在2和3之间，函数的值是2，类似在-ve端在-1和0之间，函数的值为-1。因此，如果我们讨论函数的域，则该域是实数值的整个值，但此函数的范围仅是整数，该函数将仅采用整数值，因为它是x的最大整数。现在让我们讨论这个特定函数。首先我们要讨论整数点，因此首先要检查整数点的可微性。如我们所知，函数是可微的，函数应该首先连续，如我们在点x = 1处看到的图

At integer point,

Consider x =1 

RHL = lim_{x -> 1⁺} [x] = 1

LHL = lim_{x -> 1^–} [x] = 0 

So, RHL ≠ LHL    

检查x = 1，但对所有整数点均有效，结果将相同。 [x]在整数点处不连续，因此在整数点处不可微分。因此，[x]在整数点处不连续。在整数点上也是不可微分的。

现在，让我们找到非整数点上正在发生的事情。让我们考虑x = 2.5，让我们找到RHL和LHL

RHL = lim_{x -> 2.5⁺} [x] = 2

LHL = lim_{x -> 2.5^–} [x] = 2   

由于RHL和LHL相等，因此我们的函数[x]在非整数点处是连续的。现在我们必须检查非整数点的可微性，因此我们必须找到函数的斜率，该斜率可以通过在点2.5处找到函数[x]的导数来找到

f'(x) = d[x] / dx at x = 2.5 = 0 

因此，该函数在所有非整数点上都是可微的。

2.对于f(x)= {x}

现在我们考虑第二个函数f(x)= {x} ，它是x的小数部分。为了找到可微性和连续性，我们必须先绘制图形。

因此，在此图中，函数的域是实数值的整个范围，并且该函数的范围仅是0到1，因为该值的任何小数部分都在0到1之间。让我们寻找整数值，考虑点x = 1

RHL = lim_{x -> 1⁺} {x} = 0 

LHL = lim_{x -> 1^–} {x} = 1   

由于RHL≠LHL函数{x}不连续，因此不可微。让我们寻找非整数点。考虑x = 1.5

RHL = lim_{x -> 1.5⁺} {x} = 0.5 

LHL = lim_{x -> 1.5^–} {x} = 0.5   

由于RHL = LHL，因此函数是连续的。为了找到可微性，我们必须找到函数的斜率，可以通过在点2.5处找到函数[x]的导数来找到该函数

f'(x) = d{x} / dx at x = 1.5 = 1   

因此，函数{x}在非整数点是可微的。

可微性问题

问题1：证明由f(x)= [x]定义的最大整数函数在x = 1和x = 2时不可微。

Solution:

As the question given  f(x) = [x] where x is greater than 0 and also less than 3. So we have to check the function is differentiable at point x =1 and at x = 2 or not. To check the differentiability of function, as we discussed above in Differentiation that LHD at(x=a) = RHD at (x=a) which means,

Lf’ at (x = a) = Rf’ at (x = a) if they are not equal after solving and putting the value of a in place of x then our function should not differentiable and if they both comes equal then we can say that the function is differentiable at x = a, we have to solve for two points x = 1 and x = 2. Now, let’s solve for x = 1 

f(x) = [x] 

Put x = 1 + h 

Rf’ = lim_{h -> 0} f(1 + h) – f(1) 

= lim_{h -> 0} [1 + h] – [1] 

Since [h + 1] = 1 

= lim_{h -> 0} (1 – 1) / h = 0 

Lf'(1) = lim_{h -> 0} [f(1 – h) – f(1)] / -h 

= lim_{h -> 0} ( [1 – h] – [1] ) / -h

Since [1 – h] = 0 

= lim_{h -> 0} (0 – 1) / -h 

= -1 / -0 

= ∞ 

From the above solution it is seen that Rf’ ≠ Lf’, so function f(x) = [x] is not differentiable at x = 1. Now, let’s check for x = 2. As we solved for x = 1 in the same we are going to solve for x = 2. The condition should be the same we have to check that, Lf’ at (x = 2) = Rf’ at (x = 2) or not if they are equal then our function is differentiable at x = 2 and if they are not equal our function is not differentiable at x = 2. So, let’s solve.

f(x) = [x] 

Differentiability at x=2 

Put x = 2+h 

Rf'(1) = lim_{h -> 0} f(2 + h) – f(2) 

= lim_{h -> 0} ([2 + h] – [2]) / h 

Since 2 + h = 2  

= lim_{h -> 0} (2 – 2) / h 

= lim_{h -> 0} 0 / h 

=0 

Lf'(1) = lim_{h -> 0} (f(2 – h) – f(2)) / -h 

= lim_{h -> 0} ([2 – h] – [2]) / -h 

= lim_{h -> 0} (1 – 2) / -h 

Since [2 – h] =1 

= -1 / -0 

= ∞ 

From the above solution it is seen that Rf'(2) ≠ Lf'(2), so f(x) = [x] is not differentiable at x = [2]

问题2：

$f(x) = \left\{\begin{matrix} x\times \frac{e^{1/x} - 1, x \neq 0}{e^{1/x} + 1, x = 0} \end{matrix}\right.$

证明上述函数在x = 0时不可导数。

Solution:

As we know to check the differentiability we have to find out Lf’ and Rf’ then after comparing them we get to know that the function is differentiable at the given point or not. So let’s first find the Rf'(0).

Rf'(0) = lim_{h -> 0} f(0 + h) – f(0) 

= lim_{h -> 0} (f(h) – f(0)) / h 

= lim_{h -> 0} h . [{(e^{(1 / h)} – 1) / (e(1 / h) + 1) } – 0]/h 

= lim_{h -> 0} (e^{(1 / h)} – 1) / (e^{(1 / h)} + 1) 

Multiply by e^{(-1 / h)} 

= lim_{h -> 0} {1 – e^{(-1 / h)} / 1 + e^{(-1 / h)}} 

= (1 – 0) / (1 + 0) 

= 1  

After solving we had find the value of Rf'(0) is 1. Now after this let’s find out the Lf'(0) and then we will check that the function is differentiable or not.

Lf'(0) = lim_{h -> 0} { f(0 – h) – f(0) } / -h 

= lim_{h -> 0} -h . [{e^{(-1 / h)} – 1 / e^{(-1 / h)} + 1} – 0] / -h 

= lim_{h -> 0} { (e^{(-1 / h)} – 1) / (e^{(-1 / h)} + 1) } 

= lim_{h -> 0} { (1 – e^(-∞)) / (1+e^(-∞))} 

= (0 – 1) / (0 + 1) 

= -1  

As we saw after solving Lf'(0) the value we get -1. Now checking if the function is differentiable or not, Rf'(0) ≠ Lf'(0) (-1≠1). Since Rf'(0) ≠ Lf'(0), so f(x) is not differentiable at x = 0.

问题3：一个函数是f(x)定义为

f(x)= 1 + x <2的x

f(x)= 5 – x的x≥2

函数f(x)是否在x = 2时可微?

Solution: 

So, for finding Lf'(2) we take the function f(x) = 1 = x, in the same way for finding Rf'(2) we take the function f(x) = (5 – x). Let’s find out Lf'(2) and Rf'(2)

Lf'(2) = lim_{h -> 0} {f(2 – h) – f(2)} / -h 

= lim_{h -> 0} [[(2 – h) + 1] – [5 – 2]] / -h 

= lim_{h -> 0} (3 – h – 3) / -h 

= lim_{h -> 0} -h / h 

= -1

Rf'(2) = lim_{h -> 0} {f(2 + h) – f(2)} / h 

= lim_{h -> 0} [[5 – (2 + h)] – 3] / h 

=lim_{h -> 0} h / h 

= 1  

In the first line Lf'(2) after putting in the formula, for f(2) we are putting second function (5 – x). After solving the Lf'(2) we get the value -1. For calculating Rf'(2) we are using the second function 5-x and putting in the formula of Rf’, on solving the Rf'(2) we get the value 1. Since, Rf'(2) ≠ Lf'(2) so we can say the function f(x) is not differentiable at x = 2.

问题4：查找以下函数在x = 1和x = 2时是否可微?

f(x)= x，x <1

f(x)= 2 – x，1≤x≤2

f(x)= -2 + 3x – x ² ，x> 2

Solution: 

So, to check the differentiability at x = 1. We have to find out the Lf'(1) and Rf'(1). So let’s find Lf'(1) and Rf'(1). For solving we are putting the value of x which is 1 in the formula of Lf’ and Rf’. For solving Lf’ we are taking 1st function which is x because we are calculating for left-hand derivative. After putting simply solve for Lf'(1) we get the value 1. For solving Rf’ we are taking the 2cd function which is 2 – x because we are calculating for right hand derivative. After putting, simply solve for Rf'(1) we get the value -1. So, Rf'(1) ≠ Lf'(1). Hence function is not differentiable at x= 1. Now, let’s check for x = 2

Lf'(2) = lim_{h -> 0} {f(2 – h) – f(2)} / -h 

= lim_{h -> 0} {2 – (2 – h) – (2 – 2)} / -h 

= lim_{h -> 0} h / -h 

= -1 

Rf'(2) = lim_{h -> 0} { f(2 + h) – f(2) 

= lim_{h -> 0} {-2 + 3(2 + h) – (2 + h)² – (2 – 2) } / h 

= lim_{h -> 0} {-2 + 6 + 3h – (4 + h² + 4h) – 0} / h 

= lim_{h -> 0} (-h² – h) / h 

= lim_{h -> 0} -h . (h + 1) / h 

= – (0 + 1) 

= -1  

For solving Lf'(2) we are taking the (2 – x) function because this function is less than 2, and as we know for finding the left-hand derivative we have to take the function which is les than the given limit. So, after putting in the formula of Lf’, solving the problem, and after solving we get the value -1. Now, for solving Rf’, we are taking -2 + 3x – x², as we know for finding Right-hand derivative the limit should be greater than the point at which we are calculating. Now put in the formula o Rf’ and we get the value after solving is -1. So, as we saw that the Rf'(2) = Lf'(2). Hence the function f(x) is differentiable at x = 2.