逆三角函数图–三角| 12年级数学

三角函数的反函数是三角比的反函数，即sin，cos，tan，cot，sec，cosec。这些功能广泛用于物理，数学，工程和其他研究领域。逆三角函数有两种常用的表示法：

Adding “arc” as a prefix.

Example: arcsin(x), arccos(x), arctan(x), …

Adding “-1” as superscript.

Example: sin^-1(x), cos^-1(x), tan^-1(x), …

在本文中，我们将学习图和各种反函数的性质。

正弦函数的逆，y = sin ^-1 (x)

sin ^-1 (x)是sin(x)的反函数。它的域是[-1，1]，范围是[-π/ 2，π/ 2]。它与(0,0)处的坐标轴相交。它是一个奇数函数，在(-1，1)中严格增加。

函数

函数分析

Domain	$x ∈ [−1, 1]$
Range	$y ∈ \big[\frac{−\pi}{2}, \frac{\pi}{2}\big]$
X – Intercept	$x = 0$
Y – Intercept	$y = 0$
Minima	$\big(−1, \frac{−\pi}{2}\big)$
Maxima	$\big(1, \frac{\pi}{2}\big)$
Inflection Points	$(0, 0)$
Parity	Odd Function
Monotonicity	In (-1, 1) strictly increasing

反正弦函数的样本问题

问题1：找到给定方程式的主值：

y =罪^-1 (1 /√2)

解决方案：

We are given that:

y = sin^-1(1/√2)

So we can say that,

sin(y) = (1/√2)

We know that the range of the principal value branch of sin^-1(x) is (−π/2, π/2) and sin(π/4) = 1/√2.

So, the principal value of sin^-1(1/√2) = π/4.

问题2：找到给定方程式的主值：

y =罪^-1 (1)

解决方案：

We are given that:

y = sin^-1(1)

So we can say that,

sin(y) = 1

We know that the range of the principal value branch of sin^-1(x) is (−π/2, π/2) and sin(π/2) = 1.

So, the principal value of sin^-1(1) = π/2.

余弦函数的逆，y = cos ^-1 (x)

cos ^-1 (x)是cos(x)的反函数。它的域是[-1，1]，范围是[0，π]。它与(1，π/ 2)处的坐标轴相交。它既不是偶数也不是奇函数，并且在(-1，1)中严格减小。

函数

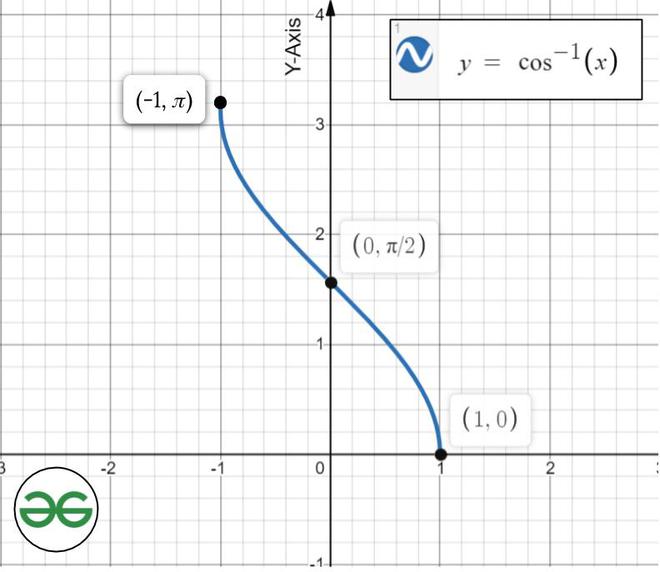
函数分析

Domain	$x ∈ [−1, 1]$
Range	$y ∈ [0, \pi]$
X – Intercept	$x = 1$
Y – Intercept	$y = \frac{\pi}{2}$
Minima	$(1, 0)$
Maxima	$(-1, \pi)$
Inflection Points	$\big(0, \frac{\pi}{2}\big)$
Parity	Neither Even Nor Odd
Monotonicity	In (-1, 1) strictly decreasing

反余弦函数的样本问题

问题1：找到给定方程式的主值：

y = cos ^-1 (1 /√2)

解决方案：

We are given that:

y = cos^-1(1/√2)

So we can say that,

cos(y) = (1/√2)

We know that the range of the principal value branch of cos^-1(x) is (0, π) and cos(π/4) = 1/√2.

So, the principal value of cos^-1(1/√2) = π/4.

问题2：找到给定方程式的主值：

y = cos ^-1 (1)

解决方案：

We are given that:

y = cos^-1(1)

So we can say that,

cos(y) = 1

We know that the range of the principal value branch of cos^-1(x) is (0, π) and cos(0) = 1.

So, the principal value of cos^-1(1) = 0.

切线函数的逆，y = tan ^-1 (x)

tan ^-1 (x)是tan(x)的反函数。它的域是ℝ，范围是[-π/ 2，π/ 2]。它与(0，0)处的坐标轴相交。它是一个奇数函数，严格以(-∞，∞)递增。

函数

函数分析

Domain	$x ∈ ℝ$
Range	$y ∈ \big(\frac{-\pi}{2}, \frac{\pi}{2}\big)$
X – Intercept	$x = 0$
Y – Intercept	$y = 0$
Minima	The function does not have any minima points.
Maxima	The function does not have any maxima points.
Inflection Points	$(0, 0)$
Parity	Odd Function
Monotonicity	In (−∞, ∞) strictly Increasing
Asymptotes	$y = \frac{\pi}{2}\space and\space y= \frac{-\pi}{2}$

切函数倒数的样本问题

问题1：找到给定方程式的主值：

y =棕褐色^-1 (1)

解决方案：

We are given that:

y = tan^-1(1)

So we can say that,

tan(y) = (1)

We know that the range of the principal value branch of tan^-1(x) is (-π/2, π/2) and tan(π/4) = 1.

So, the principal value of tan^-1(1) = π/4.

问题2：找到给定方程式的主值：

y =棕褐色^-1 (√3)

解决方案：

We are given that:

y = tan^-1(√3)

So we can say that,

tan(y) = (√3)

We know that the range of the principal value branch of tan-1(x) is (-π/2, π/2) and tan(π/3) = √3.

So, the principal value of tan-1(√3) = π/3.

余割函数的逆，y =余割^-1 (x)

cosec ^-1 (x)是cosec(x)的反函数。它的域是(-∞，-1] U [1，∞)，范围是[-π/ 2，0)U(0，π/ 2]。它不拦截坐标轴。这是一个奇数在其范围内严格减少的函数。

函数

函数分析

Domain	$x ∈ (−\infin, −1] ∪ [1,\infin)$
Range	$y ∈ \big[\frac{-\pi}{2}, 0 \big) ∪ \big(0, \frac{\pi}{2}\big]$
X – Intercept	$\phi$
Y – Intercept	$\phi$
Minima	$\big(-1, \frac{-\pi}{2} \big)$
Maxima	$\big(1, \frac{\pi}{2} \big)$
Inflection Points	The function does not have any inflection points.
Parity	Odd Function
Monotonicity	In (1, ∞) it is decreasing and in (-∞, -1) it is decreasing
Asymptotes	y = 0

反余割函数的样本问题

问题1：找到给定方程式的主值：

y =毫秒^-1 (√2)

解决方案：

We are given that:

y = cosec^-1(√2)

So we can say that,

cosec(y) = (√2)

We know that the range of the principal value branch of cosec^-1(x) is [-π/2, π/2] – {0} and cosec(π/4) = √2.

So, the principal value of cosec^-1(√2) = π/4.

问题2：找到给定方程式的主值：

y = sec ^-1 (1)

解决方案：

We are given that:

y = cosec^-1(√2)

So we can say that,

cosec(y) = 1

We know that the range of the principal value branch of cosec^-1(x) is [-π/2, π/2] – {0} and cosec(π/2) = 1.

So, the principal value of cosec^-1(1) = π/2.

正割函数的逆，y =秒^-1 (x)

sec ^-1 (x)是sec(x)的反函数。它的域是(-∞，-1] U [1，∞)，范围是[0，π/ 2)U(π/ 2，π]。它不中断坐标轴，因为它是一个不连续的函数它既不是偶函数也不是奇函数，并且在其范围内严格增加。

函数

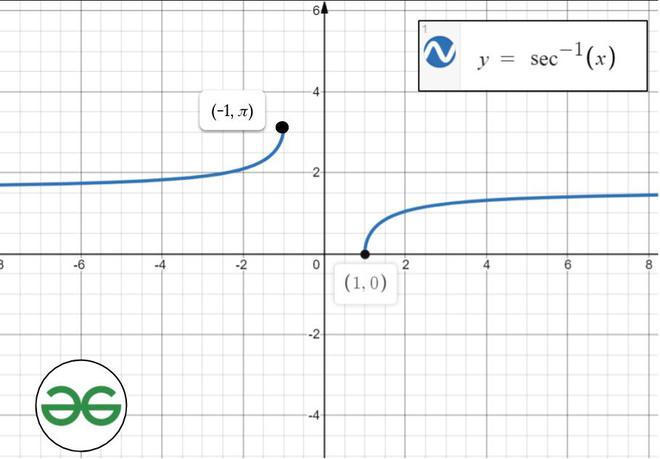
函数分析

Domain	$x ∈ (−\infin, −1] ∪ [1, \infin)$
Range	$y ∈ \big[0, \frac{\pi}{2}\big) ∪ \big(\frac{\pi}{2}, \pi\big]$
X – Intercept	$x=1$
Y – Intercept	$\phi$
Minima	$(1,0)$
Maxima	$(-1, \pi)$
Inflection Points	The function does not have any inflection points.
Parity	Neither Even Nor Odd
Monotonicity	In (1, ∞) it is increasing and in (-∞, -1) it is increasing
Asymptotes	$y = \frac{\pi}{2}$

正割函数逆的样本问题

问题1：找到给定方程式的主值：

y =秒^-1 (√2)

解决方案：

We are given that:

y = sec^-1(√2)

So we can say that,

sec(y) = (√2)

We know that the range of the principal value branch of sec^-1(x) is [0, π] – {π/2} and sec(π/4) = √2.

So, the principal value of sec^-1(√2) = π/4.

问题2：找到给定方程式的主值：

y =秒^-1 (1)

解决方案：

We are given that:

y = sec^-1(1)

So we can say that,

sec(y) = 1

We know that the range of the principal value branch of sec^-1(x) is [0, π] – {π/2} and sec(0) = 1.

So, the principal value of sec^-1(1) = 0.

余切函数的逆，y = cot ^-1 (x)

cot ^-1 (x)是cot(x)的反函数。它的域是ℝ，范围是(0，π)。它与(0，π/ 2)处的坐标轴相交。它既不是偶函数也不是奇函数，并且在其范围内严格减小。

函数

函数分析

Domain	$x ∈ ℝ$
Range	$y ∈ (0, \pi)$
X – Intercept	$x = 0$
Y – Intercept	$y = \frac{\pi}{2}$
Minima	The function does not have any minima points.
Maxima	The function does not have any maxima points.
Inflection Points	The function does not have any inflection points.
Parity	Neither Even Nor Odd
Monotonicity	In (-∞, ∞) strictly decreasing
Asymptotes	$y = 0\space and\space y = \pi$

余切函数逆的样例问题

问题1：找到给定方程式的主值：

y =婴儿床^-1 (1)

解决方案：

We are given that:

y = cot^-1(1)

So we can say that,

cot(y) = 1

We know that the range of the principal value branch of cot^-1(x) is (-π/2, π/2) and cot(π/4) = 1.

So, the principal value of cot^-1(1) = π/4.

问题2：找到给定方程式的主值：

y =婴儿床^-1 (1 /√3)

解决方案：

We are given that:

y = cot^-1(1/√3)

So we can say that,

cot(y) = (1/√3)

We know that the range of the principal value branch of cot^-1(x) is (-π/2, π/2) and cot(π/3) = 1/√3.

So, the principal value of cot^-1(1/√3) = π/3.