问题17.区分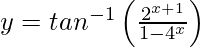 ,相对于x,-∞<x <0。
,相对于x,-∞<x <0。
解决方案:
We have,![]() , −∞ < x < 0
, −∞ < x < 0
On putting 2x = tan θ, we get,
![]()
=![]()
Now, −∞ < x < 0
=> 0 < 2x < 1
=> 0 < θ < π/4
=> 0 < 2θ < π/2
So, y = 2θ
= 2 tan−1 (2x)
Differentiating with respect to x, we get,
![]()
=![]()
=![]()
问题18.区分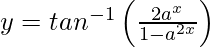 ,相对于x,a> 1,-∞
,相对于x,a> 1,-∞
解决方案:
We have,![]() , −∞ < x < 0
, −∞ < x < 0
On putting ax = tan θ, we get,
![]()
=![]()
Now, −∞ < x < 0
=> 0 < ax < 1
=> 0 < θ < π/4
=> 0 < 2θ < π/2
So, y = 2θ
= 2 tan−1 (ax)
Differentiating with respect to x, we get,
![]()
=![]()
=![]()
问题19.区分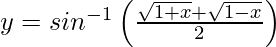 ,相对于x,0
,相对于x,0
解决方案:
We have,![]() , 0 < x < 1
, 0 < x < 1
On putting x = cos 2θ, we get,
![]()
=![]()
=![]()
=![]()
=![]()
Now, 0 < x < 1
=> 0 < cos 2θ < 1
=> 0 < 2θ < π/2
=> 0 < θ < π/4
=> π/4 < (θ+π/4) < π/2
So, y =![]()
=![]()
Differentiating with respect to x, we get,
![]()
=![]()
=![]()
问题20.区分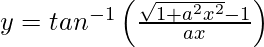 ,相对于x ,x ≠0。
,相对于x ,x ≠0。
解决方案:
We have,![]()
On putting ax = tan θ, we get,
![]()
=![]()
=![]()
=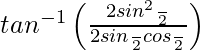
=![]()
=![]()
=![]()
Differentiating with respect to x, we get,
![]()
=![]()
问题21.区分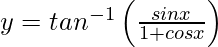 ,相对于x,-π<x <π。
,相对于x,-π<x <π。
解决方案:
We have,![]() , −π < x < π
, −π < x < π
=![]()
=![]()
=![]()
Differentiating with respect to x, we get,
![]()
=![]()
问题22.区分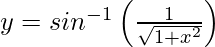 关于x。
关于x。
解决方案:
We have,![]()
On putting x = cot θ, we get,
![]()
=![]()
=![]()
= θ
= cot−1 x
Differentiating with respect to x, we get,
![]()
=![]()
问题23.区分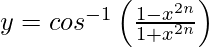 ,相对于x,0
,相对于x,0
解决方案:
We have,![]() ,0 < x < ∞
,0 < x < ∞
On putting xn = tan θ, we get,
![]()
=![]()
Now, 0 < x < ∞
=> 0 < xn < ∞
=> 0 < θ < π/2
=> 0 < 2θ < π
So, y = 2θ
= 2 tan–1 (xn)
Differentiating with respect to x, we get,
![]()
=![]()
=![]()
问题24.区分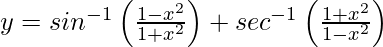 ,相对于x,x∈R。
,相对于x,x∈R。
解决方案:
We have,![]()
=![]()
=![]()
Differentiating with respect to x, we get,
![]()
= 0
问题25.区分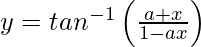 关于x。
关于x。
解决方案:
We have,![]()
=![]()
Differentiating with respect to x, we get,
![]()
= 0 +![]()
=![]()
问题26.区分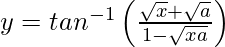 关于x。
关于x。
解决方案:
We have,![]()
=![]()
Differentiating with respect to x, we get,
![]()
=![]()
=![]()
问题27.区分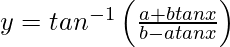 关于x。
关于x。
解决方案:
We have,![]()
=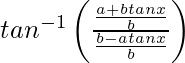
=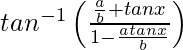
=![]()
=![]()
Differentiating with respect to x, we get,
![]()
= 0 + 1
= 1
问题28.区分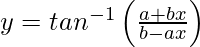 关于x。
关于x。
解决方案:
We have,![]()
=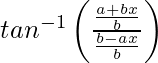
=![]()
=![]()
Differentiating with respect to x, we get,
![]()
= 0 +![]()
=![]()
问题29.区分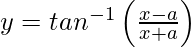 关于x。
关于x。
解决方案:
We have,![]()
=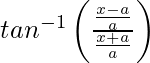
=![]()
=![]()
Differentiating with respect to x, we get,
![]()
=![]()
=![]()
=![]()
问题30.区分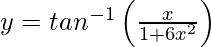 关于x。
关于x。
解决方案:
We have,![]()
=![]()
=![]()
Differentiating with respect to x, we get,
![]()
=![]()
=![]()
问题31.区分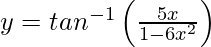 关于x。
关于x。
解决方案:
We have,![]()
=![]()
=![]()
Differentiating with respect to x, we get,
![]()
=![]()
=![]()
问题32.区分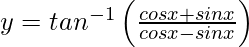 相对于x为-π/ 4 <x <π/ 4。
相对于x为-π/ 4 <x <π/ 4。
解决方案:
We have,![]() , −π/4 < x < π/4
, −π/4 < x < π/4
=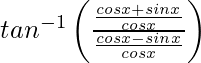
=![]()
=![]()
=![]()
=![]()
Differentiating with respect to x, we get,
![]()
= 0 + 1
= 1