问题1.给定一个圆柱罐,在哪种情况下您会找到表面积和哪种情况下的容积
(a)找出它能容纳多少。
(b)抹灰所需的水泥袋数量。
(c)找出可以装满水的较小水箱的数量。
解决方案:
a) In this condition, we will find the volume of a cylindrical tank.
b) In this condition, we will find the surface area of a cylindrical tank.
c) In this condition, we will find the volume of a cylindrical tank.
问题2.圆柱A的直径为7厘米,高度为14厘米。圆柱B的直径为14厘米,高度为7厘米。如果不做任何计算,您可以建议谁的音量更大?通过找到两个气缸的体积来验证它。检查体积较大的气缸是否也具有较大的表面积?
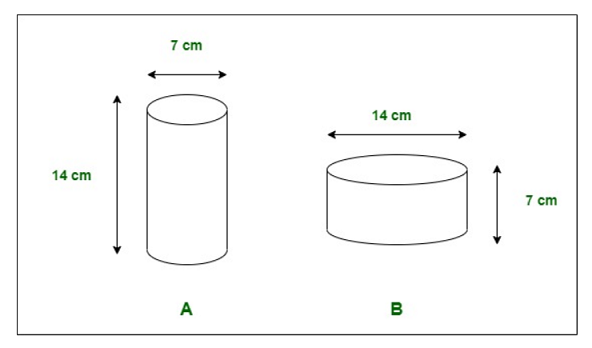
解决方案:
Cylinder A:
Radius of cylinder A = 7/2 cm
Height of cylinder A = 14 cm
Volume of cylinder A = pi.r2h = 22/7 x 7/2 x 7/2 x 14 = 539 cm3
Total Surface area of cylinder A = 2.pi.r(h + r) = 2 x 22/7 x 7/2(14 + 7/2) = 385 cm2
Cylinder B:
Radius of cylinder B = 14/2 or 7 cm
Height of cylinder B = 7 cm
Volume of cylinder B = pi.r2h = 22/7 x 7 x 7 x 7 = 1078 cm3
Total Surface area of cylinder B = 2.pi.r(h + r) = 2 x 22/7 x 7(7 + 7) = 616 cm2
We can clearly see that the Volume of cylinder B is twice that of cylinder A. Hence, verified that the Volume of cylinder B is greater than the volume of cylinder A. Also, Total surface area of cylinder B is greater.
问题3.找到一个长方体的高度,该长方体的底面积为180 cm 2 ,体积为900 cm 3 ?
解决方案:
Area of Cuboid = length x breadth = 180 cm2
Volume of Cuboid = length x breadth x height = 900 cm3
So, Area x height = Volume
180 cm2 x height = 900 cm3
Hence, height = 5 cm
Hence, height of given cuboid is 5 cm.
问题4.长方体的尺寸为60厘米×54厘米×30厘米。在给定的长方体中可以放置多少个边长6厘米的小立方体?
解决方案:
Volume of Cuboid = length x breadth x height = 60 cm x 54 cm x 30 cm = 97200 cm3
Volume of Cube = (side)3 = (6cm)3 = 216 cm3
Number of small cubes that can be placed inside given cuboid = Volume of given Cuboid/ Volume of one Cube
= 97200/216
= 450
Hence, 450 small cubes can be placed inside given cuboid.
问题5.找到圆柱体的高度,该圆柱体的体积为1.54 m 3 ,底座的直径为140 cm?
解决方案:
Volume of cylinder = 1.54 m3
Diameter of base of cylinder = 140 cm = 1.40 m, Radius = 7.20 m
As we know, Volume of cylinder = pi.r2h
So, 1.54 = 22/7 x 7.2 x 7.2 x height
On doing calculation, we get Height of cylinder = 1 m
Hence, height of given cylinder is 1 m.
问题6.奶罐为圆柱体形式,其半径为1.5 m,长度为7 m。找出可以储存在储罐中的牛奶量(以升为单位)?
解决方案:
The radius of the cylindrical tank = 1.5 m
Length/Height of cylindrical = 7 m
The quantity of milk in liters that can be stored in the tank = Volume of the cylindrical tank
So, Volume of cylinder = pi.r2h = 22/7 x 1.5 x 1.5 x 7 = 49.50 m3
Volume = 49.50 m3
As we know, 1 m3 = 1000 liters
So, 49.50 m3 = 49500 L
Hence, the quantity of milk in liters that can be stored in the tank is 49500 L
问题7.如果立方体的每个边都加倍,
(i)表面积会增加多少倍?
(ii)它的体积会增加多少倍?
解决方案:
Let us assume that the original edge of the cube is a cm. If the edge of the cube is doubled, then the new edge will be 2a cm.
i) Original surface area of cube = (edge)2 = (a)2 = a2 cm2
New surface area of cube = (edge)2 = (2a)2 = 4a2 cm2
Ratio to find which cube’s surface area is greater = Original surface area : New surface area = a2 : 4a2 = 1 : 4
Hence, surface area of cube is increased by 4 times.
ii) Original volume of cube = (edge)3 = (a)3 = a3 cm3
New volume of cube = (edge)3 = (2a)3 = 8a3 cm3
Ratio to find which cube’s volume is greater = Original volume : New volume = a3 : 8a3 = 1 : 8
Hence, volume of cube is increased by 8 times.
问题8.水以每分钟60升的速度涌入一个长方体的水库。如果水库的容量为108 m 3 ,请找到填充水库所需的小时数。
解决方案:
Given the volume of the reservoir is 108 m3 Or 108000 L [1 m3 = 1000 L]. The volume of water pouring into a cuboidal reservoir = 60 L / minutes.
So, the time is taken to fill the reservoir = Volume of cuboidal reservoir / Volume of water pouring into the reservoir per minute
= 108000/60
= 1800 minutes
= 1800/60
= 30 hours
Hence, it will require 30 hours to fill the reservoir completely.