8类NCERT解决方案–第11章测定–练习11.2

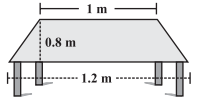
问题1.桌子顶面的形状是梯形。如果其平行边分别是1 m和1.2 m，并且它们之间的垂直距离是0.8 m，请找到其面积。

解决方案：

One parallel side of the trapezium (a) = 1 m

And second side (b) = 1.2 m and

height (h) = 0.8 m

Area of top surface of the table = (½) × (a + b)h

= (½) × (1 + 1.2)0.8

=  (½) × 2.2 × 0.8 

= 0.88

Area of top surface of the table is 0.88 m² .

问题2.梯形的面积为34 cm ² ，平行边之一的长度为10 cm，高度为4 cm求出另一平行边的长度。

解决方案：

Let the length of the other parallel side be b.

Length of one parallel side, a = 10 cm

height, (h) = 4 cm and

Area of a trapezium is 34 cm2

Formula for, Area of trapezium = (1/2) × (a + b)h

34 = ½(10 + b) × 4

34 = 2 × (10 + b)

After simplifying, b = 7

Hence another required parallel side is 7 cm.

问题3.梯形场ABCD的围栏长度为120 m。如果BC = 48 m，CD = 17 m，AD = 40 m，请找到该字段的区域。侧面AB垂直于平行侧面AD和BC。

解决方案：

Given: BC = 48 m, CD = 17 m,

AD = 40 m and perimeter = 120 m

∵ Perimeter of trapezium ABCD

= AB + BC + CD + DA

120 = AB + 48 + 17 + 40

120 = AB = 105

AB = 120 – 105 = 15 m

Now, Area of the field = (½) × (BC + AD) × AB

= (½) × (48 + 40) × 15

= (½) × 88 × 15

= 660

Hence, area of the field ABCD is 660m² 

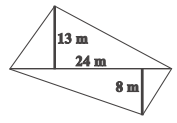
问题4.一个四边形形状的场的对角线为24 m，从其余相对顶点落在其上的垂线为8 m和13 m。查找字段的区域。

解决方案：

Consider, h1 = 13 m, h2 = 8 m and AC = 24 m

Area of quadrilateral ABCD = Area of triangle ABC + Area of triangle ADC

= ½(bh1) + ½(bh2)

= ½ × b(h1 + h2) = (½) × 24 × (13 + 8)

= (½) × 24 × 21 = 252

Hence, required area of the field is 252 m²

问题5.菱形的对角线是7.5厘米和12厘米。查找其区域。

解决方案：

Given:  d1 = 7.5 cm and d2 = 12 cm

We know that,Area of rhombus =  (½) × d1 × d2 = (½) × 7.5 × 12 = 45

Therefore, area of rhombus is 45 cm² .

问题6：找到菱形的侧面，该侧面的边长为5厘米，高度为4.8厘米。如果对角线之一长8厘米，请找出另一对角线的长度。

解决方案：

Since a rhombus is also a kind of a parallelogram.

Formula for Area of rhombus = Base × Altitude

Putting values, we have

Area of rhombus = 6 × 4 = 24

Area of rhombus is 24 cm2

Also, Formula for Area of rhombus = (½) × d1d2

After substituting the values, we get

24 = (½) × 8 × d2

d2 = 6

Hence, the length of the other diagonal is 6 cm.

问题7.建筑物的地板由3000块菱形瓷砖组成，其对角线的长度分别为45厘米和30厘米。^{如果每m 2}的成本为Rs，则求出抛光地板的总成本。 4，

解决方案：

Length of one diagonal,  d1 = 45 cm and  d2= 30 cm

∵ Area of one tile =  (½)d1d2 = (½) × 45 × 30 = 675

Area of one tile is 675 cm²

Area of 3000 tiles is

= 675 × 3000

= 2025000 cm²

= 2025000/10000

= 202.50 m2 [∵ 1m2 = 10000 cm2]

∵ Cost of polishing the floor per sq. meter = 4

Cost of polishing the floor per 202.50 sq. meter = 4 × 202.50 = 810

Hence the total cost of polishing the floor is Rs. 810.

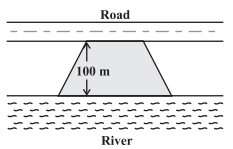
问题8.莫汉想购买一个梯形的田地。它沿河的一侧与道路平行，是沿道路的一侧的两倍。如果该区域的面积为10500 m ²且两个平行边之间的垂直距离为100 m，则求出沿河边的长度。

解决方案：

Perpendicular distance  (h) = 100 m (Given)

Area of the trapezium shaped field = 10500 m2 (Given)

Let side along the road be ‘x’ m and side along the river =  2x m

Area of the trapezium field =  (½) × (a + b) × h

10500 =  (½) × (x + 2x) × 100

10500 = 3x × 50

After simplifying, we have x = 70, which means side along the river is 70 m

Hence, the side along the river =  2x = 2(70) = 140 m.

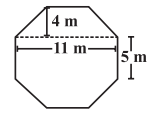
问题9.如图所示，凸起平台的顶面为正八边形。找到八边形表面的面积。

解决方案：

Octagon having eight equal sides, each 5 m. (given)

Divide the octagon as show in the below figure, 2 trapeziums whose parallel and perpendicular sides are 11 m and 4 m respectively and 3rd one is rectangle having length and breadth 11 m and 5 m respectively.

Now, Area of two trapeziums = 2 [(½) × (a + b) × h]

= 2 × (½) × (11 + 5 ) × 4

= 4 × 16 = 64

Area of two trapeziums is 64 m²

Also, Area of rectangle = length × breadth

= 11 × 5 = 55

Area of rectangle is 55 m²

Total area of octagon = 64 + 55

= 119 m²

问题10.如图所示，有一个五边形的公园。

为了找到其区域，Jyoti和Kavita用两种不同的方式对其进行了划分。两种方法都可以找到这个公园的区域。您能建议其他找到其区域的方法吗?

解决方案：

First way:  By Jyoti’s diagram,

Area of pentagon = Area of trapezium ABCP + Area of trapezium AEDP

=  (½)(AP + BC) × CP + (1/2) × (ED + AP) × DP

=  (½)(30 + 15) × CP + (1/2) × (15 + 30) × DP

=  (½) × (30 + 15) × (CP + DP)

=  (½) × 45 × CD

= (1/2) × 45 × 15

= 337.5 m2

Area of pentagon is 337.5 m²

Second way: By Kavita’s diagram

Here, a perpendicular AM drawn to BE.

AM = 30 – 15 = 15 m

Area of pentagon = Area of  triangle ABE + Area of square BCDE (from above figure)

= (½) × 15 × 15 + (15 × 15)

= 112.5 + 225.0

= 337.5

Hence, total area of pentagon shaped park = 337.5 m2

问题11.相邻相框的示意图的外部尺寸为24 cm×28 cm，内部尺寸为16 cm×20 cm。如果每个部分的宽度相同，请找到框架每个部分的面积。

解决方案：

Divide given figure into 4 parts, as shown below:

Here two of given figures (I) and (II) are similar in dimensions.

And also figures (III) and (IV) are similar in dimensions.

Area of figure (I) = Area of trapezium

=  (½) × (a + b) × h

= (½) × (28 + 20) × 4

=  (½) × 48 × 4 = 96

Area of figure (I) = 96 cm²

Also, Area of figure (II) = 96 cm²

Now, Area of figure (III) = Area of trapezium

= (½) × (a + b) × h

= (½) × (24 + 16)4

= (½) × 40 × 4 = 80

Area of figure (III) is 80 cm²

Also, Area of figure (IV) = 80 cm²