问题1.如图所示,有两个长方体的盒子。哪个盒子需要制作的材料数量更少?

解决方案:
(a) For finding which box requires the lesser amount of material to make we have to calculate total surface area of both these boxes.
So, Length of first cuboidal box (l) = 60 cm
Breadth of first cuboidal box (b) = 40 cm
Height of first cuboidal box (h) = 50 cm
Total surface area of first cuboidal box = 2 × (lb + bh + hl)
= 2 × (60 × 40 + 40 × 50 + 50 × 60)
= 2 × (2400 + 2000 + 3000)
= 14800 cm2
Total surface area of first cuboidal box is 14800 cm².
(b) Also,
Length of second cubical box (l) = 50 cm
Breadth of second cubicalbox (b) = 50 cm
Height of second cubicalbox (h) = 50 cm
Total surface area of second cubical box = 6 (side)2
= 6 (50 × 50)
= 6 × 2500
= 15000 cm²
Total surface area of the second cubical box is 15000 cm2
From both of these result we found that cuboidal box (observation “a”) requires the lesser amount of material to make.
问题2.行李箱尺寸为80厘米×48厘米×24厘米,应盖上防水布。覆盖100个这样的手提箱,需要多少米的宽度为96厘米的防水油布?
解决方案:
Length of suitcase box (l)= 80 cm,
Breadth of suitcase box (b) = 48 cm
Height of cuboidal box (h) = 24 cm
Total surface area of suitcase box = 2 × (lb + bh + hl)
= 2 × (80 × 48 + 48 × 24 + 24 × 80)
= 2 × (3840 + 1152 + 1920)
= 2 × 6912
= 13824 cm²
Hence, Total surface area of suitcase box is 13824 cm²
As suitcase is fully covered by tarpaulin
Area of Tarpaulin cloth = Surface area of suitcase
(l × b) = 13824
(l × 96) = 13824
l = 144m
Required tarpaulin for 100 suitcases = 144 × 100 = 14400 cm = 144 m
Hence, tarpaulin cloth required to cover 100 suitcases is 144 m.
问题3.找到一个表面积为600平方厘米的立方体的一面。
解决方案:
Given that
Surface area of cube = 600 cm²
Formula for surface area of a cube = 6(side)²
Substituting the values, we get
6 × (side)² = 600
(side)² = 100
Or side = ±10
We can’t take side as negative
Hence, the measure of each side of a cube is 10 cm
问题4. Rukhsar绘制了尺寸为1 m×2 m×1.5 m的机柜外部。如果涂除柜子底部以外的所有涂料,她将覆盖多少表面积。
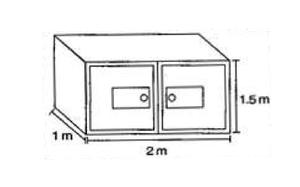
解决方案:
Length of cabinet (l) = 2 m,
Breadth of cabinet (b) = 1 m,
and Height of cabinet (h) = 1.5 m
Surface area of cabinet = 2 × (lb + bh + hl) – lb
= 2 × (2 × 1 + 1 × 1.5 + 1.5 × 2) – 2 × 1
= 2 × (2 + 1.5 + 3.0) – 2
= 2 × (6.5) – 2
= 13 – 2
= 11m²
Required surface area of cabinet is 11m²
问题5.丹尼尔正在画一个长方体的墙壁和天花板,长,宽和高分别为15 m,10 m和7 m。从每罐油漆中涂100平方米的面积。她需要给房间涂几罐油漆?
解决方案:
Length of wall (l) = 15 m,
Breadth of wall (b) = 10 m
Height of wall, (h) = 7 m
Total Surface area of classroom = 2 × (lb + bh + hl) – lb
= 2 × (15 × 10 + 10 × 7 + 7 × 15) – (15 × 10)
= 2 × (150 + 70 + 105) – 150
= 650 – 150
= 500
Now, Required number of cans = Area of hall/Area of one can
= 500/100 = 5
Therefore, 5 cans are required to paint the room.
问题6.描述右边的两个数字是如何相似的,以及它们是如何不同的。哪个盒子的侧面面积更大?
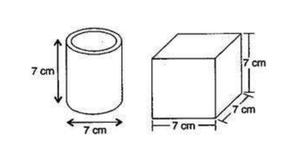
解决方案:
Given that,
Diameter of cylinder = 7 cm
Radius of cylinder (r) = 7 / 2 cm
Height of cylinder (h) = 7 cm
Surface area of cylinder = 2πrh
= 2 × (22 / 7) × (7 / 2) × 7 = 154
So, Lateral surface area of cylinder is 154 cm²
Now, lateral surface area of cube = 4 (side)² = 4 × 72 = 4 × 49 = 196
Lateral surface area of cube is 196 cm²
Hence, the cube has larger lateral surface area.
问题7:一个半径7 m,高度3 m的封闭圆筒形水箱由一块金属制成。有多少的金属片所需要的?

Radius of cylindrical tank (r) = 7 m
Height of cylindrical tank (h) = 3 m
Total surface area of cylindrical tank = 2πrh + 2πr² = 2πr × (h + r)
= 2 × (22 / 7) × 7 (3 + 7)
= 44 × 10 = 440
Therefore, 440 m² metal sheet is required.
问题8.中空圆柱体的侧面面积为4224平方厘米。沿其高度切割,并形成一块宽度为33厘米的矩形板。找到矩形板的周长?
解决方案:
Lateral surface area of hollow cylinder = 4224 cm²
Height of hollow cylinder, h = 33 cm
and say r be the radius of the hollow cylinder
Curved surface area of hollow cylinder = 2πrh
4224 = 2 × π × r × 33
r = (4224) / (2π × 33)
r = 64 × 7/ 22
Now, Length of rectangular sheet, l = 2πr
l = 2 × 22 / 7× (64 × 7/ 22) = 128
So the length of the rectangular sheet is 128 cm.
Also, Perimeter of rectangular sheet = 2 × (l + b)
= 2 × (128 + 33)
= 322
The perimeter of rectangular sheet is 322 cm.
问题9.压路机需要经过750次完整的旋转才能平整道路。如果压路机的直径为84厘米,长度为1 m,请找到道路区域。

解决方案:
Diameter of road roller (d) = 84 cm
Radius of road roller (r) = d / 2 = 84 / 2 = 42 cm
Length of road roller (h) = 1 m = 100 cm
Curved surface area of road roller = 2πrh
= 2 × (22 / 7) × 42 × 100 = 26400
Curved surface area of road roller is 26400 cm²
Again, Area covered by road roller in 750 revolutions = 26400 × 750cm²
= 1,98,00,000 cm²
= 1,98,00,000 × (1 / 10,000) m² (1cm²= 1 / 10,000m²)
Hence, the area of the road is 1980 m².
问题10.一家公司将其奶粉包装在圆柱形容器中,该容器的底部直径为14厘米,高度为20厘米。公司在容器表面周围放置一个标签(如图所示)。如果将标签放置在距顶部和底部2厘米处,标签的面积是多少?
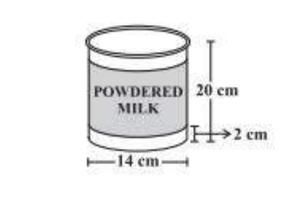
解决方案:
Diameter of cylindrical container (d) = 14 cm
Radius of cylindrical container (r) = d / 2 = 14 / 2 = 7 cm
Height of cylindrical container (H) = 20 cm
Height of the label (h) = Height of container – free space
= 20 – 2 (2)
= 16 cm
Area of label = 2πrh
= 2 × (22 / 7) × 7 × 16
= 704 cm²
Hence, the area of the label is 704 cm².