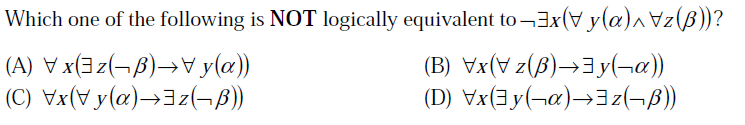
(一) A
(乙)乙
(C)丙
(四)丁答案: (A) (D)
解释:
给定的陈述是:
¬ ∃ x ( ∀y(α) ∧ ∀z(β) )
where ¬ is a negation operator, ∃ is Existential Quantifier with the
meaning of "there Exists", and ∀ is a Universal Quantifier
with the meaning " for all " , and α, β can be treated as predicates.
here we can apply some of the standard
results of Propositional and 1st order logic on the given statement,
which are as follows :
[ Result 1 : ¬(∀x P(x)) <=> ∃ x¬P(x), i.e. negation
of "for all" gives "there exists" and negation also gets applied to scope of
quantifier, which is P(x) here. And also negation of "there exists" gives "for all",
and negation also gets applied to scope of quantifier ]
[ Result 2 : ¬ ( A ∧ B ) = ( ¬A ∨ ¬B ) ]
[ Result 3 : ¬P ∨ Q <=> P -> Q ]
[ Result 4 : If P ->Q, then by Result of Contrapositive, ¬Q -> ¬P ]
现在我们需要使用这些结果,如下所示:
¬ ∃ x ( ∀y(α) ∧ ∀z(β) ) [ Given ]
=> ∀ x (¬∀y(α) ∨ ¬∀z(β) ) [ after applying Result 1 & Result 2 ]
=> ∀ x ( ∀y(α) -> ¬∀z(β) ) [after applying Result 3 ]
=> ∀ x ( ∀y(α) -> ∃z(¬β) ) [after applying Result 1]
which is same as the statement C.
Hence the Given Statement is logically Equivalent
to the statement C.
Now, we can also prove that given statement is logically equivalent to the statement
in option B.
Let's see how !
The above derived statement is :
∀ x ( ∀y(α) -> ∃z(¬β) )
Now this statement can be written as (or equivalent to) :
=> ∀ x ( ∀z(β) -> ∃y(¬α) ) [after applying Result 4 ]
And this statement is same as statement B.
Hence the Given statement is also logically equivalent
to the statement B.
So, we can conclude that the Given statement is NOT logically equivalent to the
statements A and D.
因此,正确答案是选项 A 和选项 D。但在 GATE 2013 中,标记
所有人都回答了这个问题。
这个问题的测验