第 11 课 RD Sharma 解——第 15 章线性不等式——练习 15.6

问题 1(i)。以图形方式求解以下线性不等式系统：

2x + 3y ≤ 6

3x + 2y ≤ 6

x≥0，y≥0

解决方案：

Let us convert the given inequations to equations.

2x + 3y = 6             -(1)

3x + 2y = 6             -(2)

x = 0                    -(3)

y = 0                    -(4)

Let us consider eq(1)

The line 2x + 3y = 6 meets the x-axis at (3, 0) and the y-axis at (0, 2).

And Origin(0, 0) satisfies the inequation 2x + 3y ≤ 6.

So, the section containing the origin will represent the solution set of inequation 2x + 3y ≤ 6.

Let us consider eq(2)

The line 3x + 2y = 6 meets the x-axis at (2, 0) and the y-axis at (0, 3).

And Origin(0, 0) satisfies the inequation 3x + 2y ≤ 6.

So, the section containing the origin will represent the solution set of inequation 3x + 2y ≤ 6.

x ≥ 0 and y ≥ 0 represent the first quadrant.

Thus, the shaded region represents the solution of the given inequations.

问题 1(ii)。以图形方式求解以下线性不等式系统：

2x + 3y ≤ 6

x + 4y ≤ 4

x≥0，y≥0

解决方案：

Let us convert the given inequations to equations.

2x + 3y = 6       -(1)

x + 4y = 4         -(2)

x = 0              -(3)

y = 0              -(4)

Let us consider eq(1) 

The line 2x + 3y = 6 meets the x-axis at (3, 0) and the y-axis at (0, 2).

And Origin(0, 0) satisfies the inequation 2x + 3y ≤ 6.

So, the section containing the origin will represent the solution set of inequation 2x + 3y ≤ 6.

Let us consider eq(2)

The line x + 4y = 4 meets the x-axis at (4, 0) and the y-axis at (0, 1).

And Origin(0, 0) satisfies the inequation x + 4y ≤ 4.

So, the section containing the origin will represent the solution set of inequation x + 4y ≤ 4.

x ≥ 0 and y ≥ 0 represent the first quadrant.

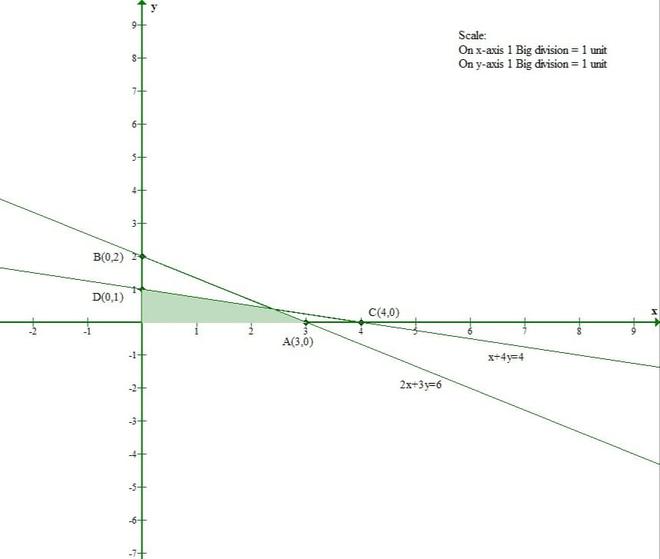
Thus, the shaded region represents the solution set of given inequations.

问题 1(iii)。以图形方式求解以下线性方程组：

x – y ≤ 1

x + 2y ≤ 8

2x + y ≥ 2

x≥0，y≥0

解决方案：

Let us convert the given inequations to equations.

x – y = 1              – (1)

x + 2y = 8            -(2)

2x + y = 2              -(3)

x = 0, y = 0             -(4)

Let us consider eq(1)

The line x – y = 1 meets the x-axis at (1, 0) and the y-axis at (0, -1).

And Origin(0, 0) satisfies the inequation x – y ≤ 1

So, the section containing the origin will represent the solution set of inequation x – y ≤ 1.

Let us consider eq(2)

The line x + 2y = 8 meets the x-axis at (8, 0) and the y-axis at (0, 4).

And Origin(0, 0) satisfies the inequation x + 2y ≤ 8.

So, the section containing the origin will represent the solution set of inequation  x + 2y ≤ 8.

Let us consider eq(3)

The line 2x + y = 2 meets the x-axis at (1, 0) and the y-axis at (0, 2).

And Origin(0, 0) doesnot satisfy the inequation 2x + y ≥ 2.

So, the section containing the origin will represent the solution set of inequation 2x + y ≥ 2.

x ≥ 0 and y ≥ 0 represent the first quadrant.

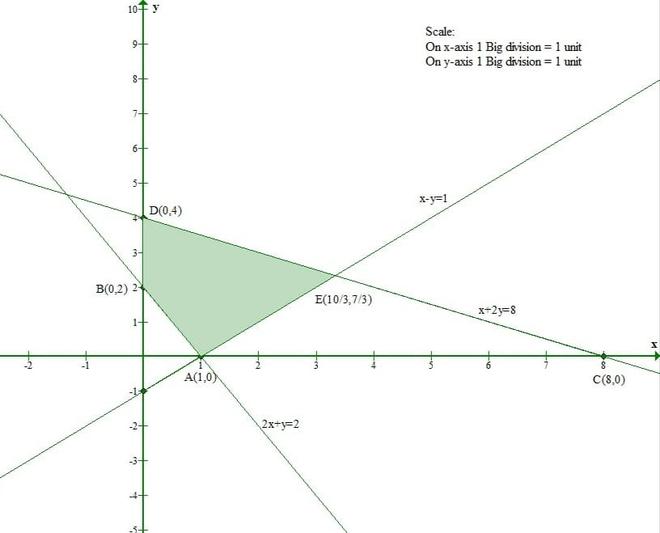
Thus the shaded region represents the solution set of given inequations.

问题 1(iv)。以图形方式求解以下线性方程组：

x + y ≥ 1

7x + 9y ≤ 63

x ≤ 6

y≤5

x≥0，y≥0

解决方案：

Let us convert the given inequations to equations.

x + y = 1                      -(1)

7x + 9y = 63                 -(2)

x = 6                           -(3)

y = 5                          -(4)

x = 0, y = 0

Let us consider eq(1)

The line x + y= 1 meets the x-axis at (1, 0) and the y-axis at (0, 1).

And Origin(0, 0) doesnot satisfy the inequation x + y ≥ 1.

So, the section containing the origin will represent the solution set of inequation x + y ≥ 1.

Let us consider eq(2)

The line 7x + 9y = 63 meets the x-axis at (9, 0) and the y-axis at (0, 7).

And Origin(0, 0) satisfies the inequation 7x + 9y ≤ 63.

So, the section containing the origin will represent the solution set of inequation 7x + 9y ≤ 63.

Let us consider eq(3)

The line x = 6 is parallel to y-axis and it is at a distance of 6 units from it.

And Origin(0, 0) satisfies the inequation x ≤ 6.

So, the section containing the origin will represent the solution set of inequation x ≤ 6.

Let us consider eq(4)

The line y = 5 is parallel to x-axis and it is at a distance of 5 units from it.

And Origin(0, 0) satisfies the inequation y ≤ 5.

So, the section containing the origin will represent the solution set of inequation y ≤ 5.

x ≥ 0 and y ≥ 0 represent the first quadrant.

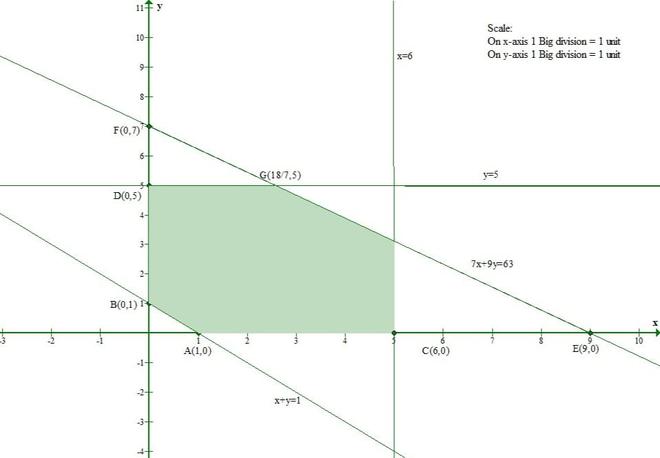
Thus, the shaded region represents the solution sets of given inequations.

问题 1(v)。以图形方式求解以下线性方程组：

2x + 3y ≤ 35

y≥3

x≥2

x≥0，y≥0

解决方案：

Let us convert the given inequations to equations.

2x + 3y = 35                 -(1)

y = 3                          -(2)

x = 2                           -(3)

x = 0, y = 0

Let us consider eq(1)

The line 2x + 3y = 35 meets the x-axis at (35/2, 0) and the y-axis at (0, 35/3).

And Origin(0, 0) satisfies the inequation 2x + 3y ≤ 35.

So, the section containing the origin will represent the solution set of inequation  2x + 3y ≤ 35.

Let us consider eq(2)

The line y = 3 is parallel to x-axis and it is at a distance of 3 units from it.

And Origin(0, 0) doesnot satisfy the inequation y ≥ 3.

So, the section containing the origin will represent the solution set of inequation  y ≥ 3.

Let us consider eq(3)

The line x = 2 is parallel to y-axis and it is at a distance of 2 units from it.

And Origin(0, 0) doesnot satisfy the inequation x ≥ 2.

So, the section containing the origin will represent the solution set of inequation  x ≥ 2.

x ≥ 0 and y ≥ 0 represent the first quadrant.

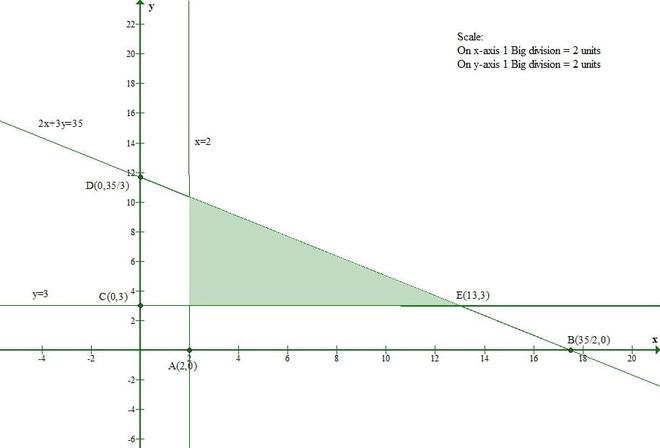
Thus, the shaded region represents the solution sets of given inequations.

问题 2(i)。证明下列线性方程组的解集是空集：

x – 2y ≥ 0

2x – y ≤ -2

x ≥ 0

y≥0

解决方案：

Let us convert the given inequations to equations.

x – 2y = 0                  –(1)

2x – y = -2                  -(2)

x = 0                        -(3)

y = 0                       -(4)

Let us consider eq(1)

The line x – 2y = 0 meets the x-axis at (0, 0) and the y-axis at (0, 0).

If x = 1 then y = 1/2

And Origin(0, 0) satisfies the inequation x – 2y ≥ 0.

So, the section containing the origin will represent the solution set of inequation x – 2y ≥ 0.

Let us consider eq(2)

The line 2x – y = -2 meets the x-axis at (-1, 0) and y-axis at (0, 2).

And Origin(0, 0) doesn’t satisfy the inequation 2x – y ≤ -2.

So, the section containing the origin will represent the solution set of inequation 2x – y ≤ -2.

Clearly, x ≥ 0 and y ≥ 0 represent the first quadrant.

From the given graph we conclude that there is no common region in all the lines.

So, the solution set to given inequations is empty.

Hence Proved

问题 2(ii)。证明下列线性方程组的解集是空集：

x + 2y ≤ 3

3x + 4y ≥ 12

y≥1

x ≥ 0

y≥0

解决方案：

Let us convert the given inequations to equations.

x + 2y = 3                        -(1)

3x + 4y = 12                     -(2)

y = 1                               -(3)

x = 0                               -(4)

y = 0                               -(5)

Let us consider eq(1)

The line x + 2y = 3 meets the x-axis at (3, 0) and the y-axis at (0, 3/2).

And Origin(0, 0) satisfies the inequation x + 2y ≤ 3.

So, the section containing the origin will represent the solution set of inequation x + 2y ≤ 3.

Let us consider eq(2)

The line 3x + 4y = 12 meets the x-axis at (4, 0) and y-axis at (0, 3).

And Origin(0, 0) doesnot satisfy the inequation 3x + 4y ≥ 12.

So, the section containing the origin will represent the solution set of inequation 3x + 4y ≥ 12.

Let us consider eq(3)

The line y = 1 is parallel to x-axis and it is at a distance of 1 unit from it.

And Origin(0, 0) doesnot satisfy the inequation y ≥ 1.

So, the section containing the origin will represent the solution set of inequation y ≥ 1.

x ≥ 0 and y ≥ 0 represent the first quadrant.

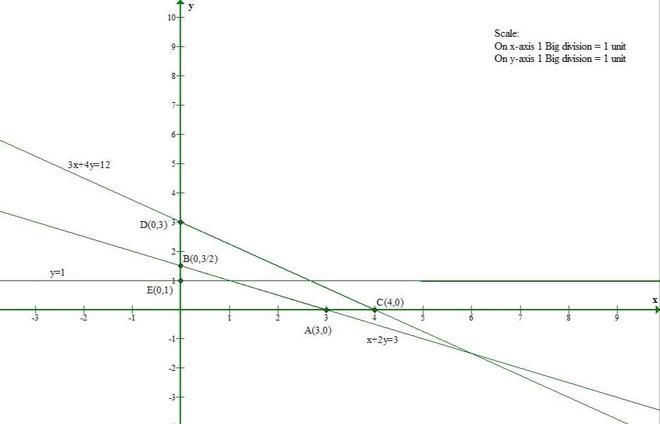
From the given graph we conclude that there is no common region in all the lines.

So, the solution set to given inequations is empty.

Hence Proved

问题 3. 找出下图中阴影区域为解集的线性不等式。画出线性不等式的解集图。

解决方案：

Let us consider the line 2x + 3y = 6

The shaded region and origin(0, 0) are on the opposite side of this line.

And Origin(0, 0) doesnot satisfy the inequation 2x + 3y ≥ 6

Let us consider the line 4x + 6y = 24

The shaded region and origin (0, 0) are on the same side of this line.

And Origin(0, 0) satisfies the inequation 4x + 6y ≤ 24

Let us consider the line x – 2y = 2

The shaded region and origin (0, 0) are on the same side of this line.

And Origin(0, 0) satisfies the inequation x – 2y ≤ 2

Let us consider the line -3x + 2y = 3

The shaded region and origin (0, 0) are on the same side of this line.

And Origin(0, 0) satisfies the inequation -3x + 2y ≤ 3

Since the shaded part is in the first quadrant.

We also have to take x ≥ 0 and y ≥ 0.

Thus, the linear equations comprising the given solution set are:

2x + 3y ≥ 6, 4x + 6y ≤ 24, x – 2y ≤ 2, -3x + 2y ≤ 3,  x ≥ 0 and y≥. 0.

问题 4. 找出解集是下面给出的阴影区域的线性不等式。

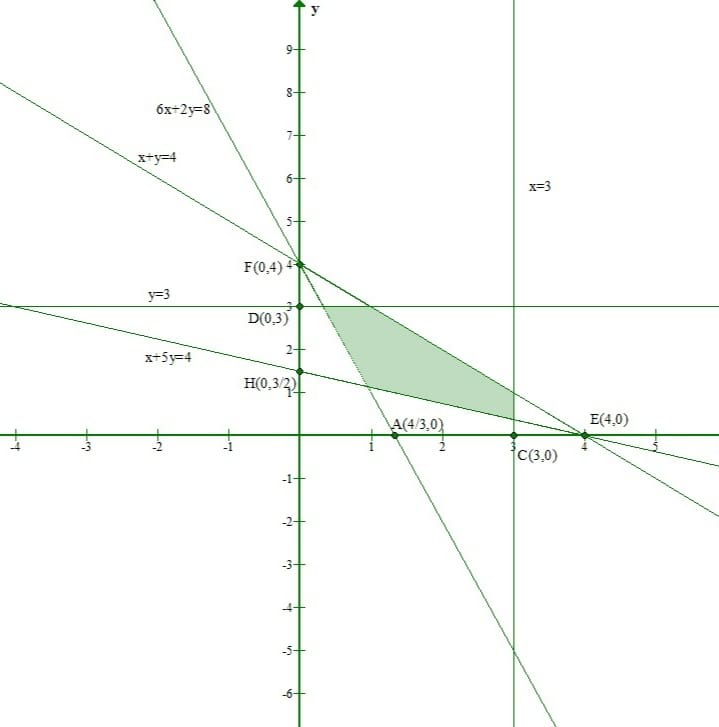
解决方案：

Let us consider line x + y = 4

The shaded region and origin (0, 0) are on the same side of this line.

And Origin(0, 0) doesnot satisfy the inequation x + y ≤ 4

Let us consider line y = 3

The shaded region and origin (0, 0) are on the same side of this line.

And Origin(0, 0) satisfies the inequation y ≤ 3.

Let us consider line x = 3

The shaded region and origin (0, 0) are on the same side of this line.

And Origin(0, 0) satisfies the inequation x ≤ 3.

Let us consider line x + 5y = 4

The shaded region and origin (0, 0) are on the opposite side of this line.

And Origin(0, 0) doesnot satisfy the inequation x + 5y ≥ 4.

Let us consider line 6x + 2y = 8

The shaded region and origin (0, 0) are on the opposite side of this line.

And Origin(0, 0) doesnot satisfy the inequation 6x + 2y ≥ 8.

Since the shaded part is in the first quadrant.

We also have to take x ≥ 0 and y ≥ 0.

Thus, the linear equations comprising the given solution set are:

x + y ≤ 4, x ≤ 3, y ≤ 3 x + 5y ≥ 4, 6x + 2y ≥ 8, x ≥ 0 and y ≥ 0.

问题 5. 证明下列线性不等式的解集是一个无界集：

x + y ≥ 9

3x + y ≥ 12

x ≥ 0 和 y ≥ 0。

解决方案：

Let us convert the given inequations to equations.

x + y = 9                           -(1)

3x + y = 12                        -(2)

x = 0 and y = 0                  -(3)

Let us consider eq(1)

The line x + y = 9 meets the x-axis at (9, 0) and the y-axis at (0, 9).

And Origin(0, 0) doesnot satisfy the inequation x + y ≥ 9.

So, the section containing the origin will represent the solution set of inequation x + y ≥ 9.

Let us consider eq(2)

The line 3x + y = 12 meets the x-axis at (4, 0) and y-axis at (0, 12).

And Origin(0, 0) doesnot satisfy the inequation 3x + y ≥ 12.

So, the section containing the origin will represent the solution set of inequation 3x + y ≥ 12.

Clearly, x ≥ 0 and y ≥ 0 represent the first quadrant.

Hence, the solution set lies in the first quadrant.

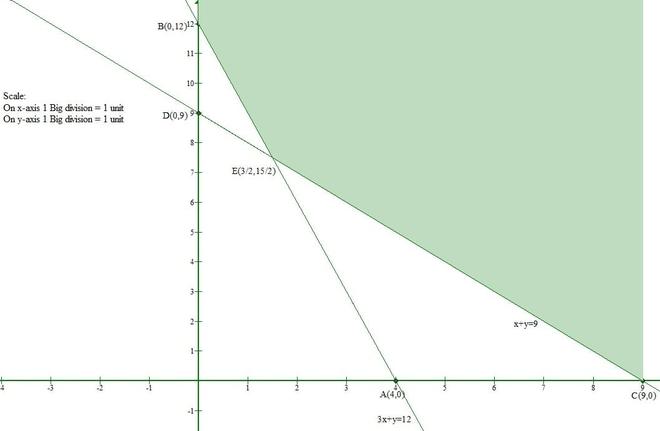
From the given graph we conclude that the shaded region is unbounded.

Hence, the solution set to the given set of inequalities is an unbounded set.

问题 6(i)。以图形方式求解以下不等式系统：

2x + y ≥ 8, x + 2y ≥ 8, x + y ≤ 6

解决方案：

Let us convert the given inequations to equations.

2x + y = 8                       -(1)

x + 2y = 8                       -(2)

x + y = 6                       -(3)

Let us consider eq(1)

The line 2x + y = 8 meets the x-axis at (4, 0) and the y-axis at (0, 8).

And Origin(0, 0) doesnot satisfy the inequation 2x + y ≥ 8.

So, the section containing the origin will represent the solution set of inequation 2x + y ≥ 8.

Let us consider eq(2)

The line x + 2y ≥ 8 meets the x-axis at (8, 0) and y-axis at (0, 4).

And Origin(0, 0) doesnot satisfy the inequation x + 2y ≥ 8.

So, the section containing the origin will represent the solution set of inequation x + 2y ≥ 8.

Let us consider eq(3)

The line x + y = 6 meets the x-axis at (6, 0) and the y-axis at (0, 6).

And Origin(0, 0) satisfies the inequation x + y ≤ 6.

So, the section containing the origin will represent the solution set of inequation x + y ≤ 6.

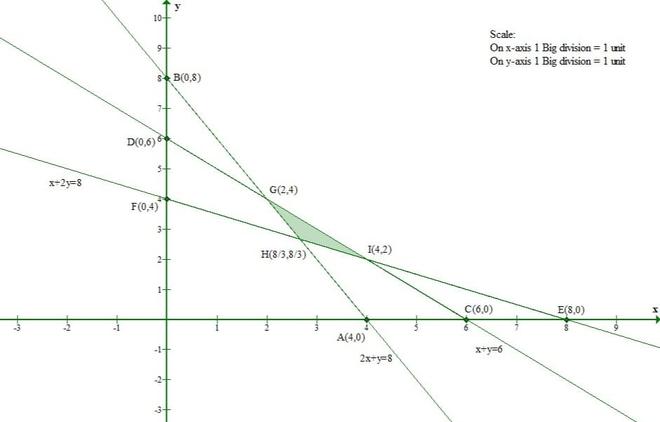
Hence, the solution set to the inequilities is the intersection of the above three solutions.

Thus, the shaded region represents the solution set of the given set of inequilities.

问题 6(ii)。以图形方式求解以下不等式系统：

12x + 12y ≤ 840, 3x + 6y ≤ 300, 8x + 4y ≤ 480, x ≥ 0 和 y ≥ 0。

解决方案：

Let us convert the given inequations to equations.

12x + 12y = 840               -(1)

 3x + 6y = 300                  -(2)

 8x + 4y = 480                  -(3)

 x = 0 and y = 0              -(4)

Let us consider eq(1)

The line 12x + 12y = 840 meets the x-axis at (70, 0) and the y-axis at (0, 70).

And Origin(0, 0) satisfies the inequation 12x + 12y ≤ 840.

So, the section containing the origin will represent the solution set of inequation 12x + 12y ≤ 840.

Let us consider eq(2)

The line 3x + 6y = 300 meets the x-axis at (100, 0) and the y-axis at (0, 50).

And Origin(0, 0) satisfies the inequation 3x + 6y ≤ 300.

So, the section containing the origin will represent the solution set of inequation 3x + 6y ≤ 300.

Let us consider eq(3)

The line 8x + 4y = 480 meets the x-axis at (60, 0) and the y-axis at (0, 120).

And Origin(0, 0) satisfies the inequation 8x + 4y ≤ 480.

So, the section containing the origin will represent the solution set of inequation 8x + 4y ≤ 480.

Clearly, x ≥ 0 and y ≥ 0 represent the first quadrant.

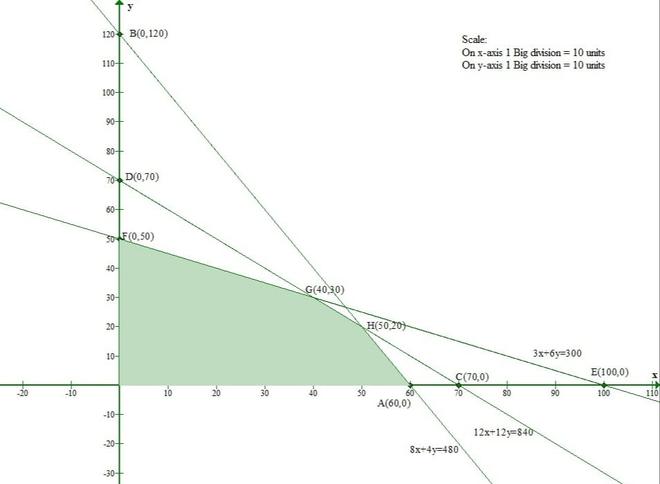
Hence, the solution set to the inequilities is the intersection of the above three solutions.

Thus, the shaded region represents the solution set of the given set of inequalities.

问题 6(iii)。以图形方式求解以下不等式系统：

x + 2y ≤ 40、3x + y ≥ 30、4x + 3y ≥ 60、x ≥ 0 和 y ≥ 0。

解决方案：

Let us convert the given inequations to equations.

x + 2y = 40                      -(1)

3x + y = 30                       -(2)

4x + 3y = 60                     -(3)

x = 0 and y = 0                 -(4)

Let us consider eq(1)

The line x + 2y = 40 meets the x-axis at (40, 0) and the y-axis at (0, 20).

And Origin(0, 0) satisfies the inequation x + 2y ≤ 40.

So, the section containing the origin will represent the solution set of inequation x + 2y ≤ 40.

Let us consider eq(2)

The line 3x + y = 30 meets the x-axis at (10, 0) and y-axis at (0, 30).

And Origin(0, 0) doesnot satisfy the inequation 3x + y ≥ 30.

So, the section containing the origin will represent the solution set of inequation 3x + y ≥ 30.

Let us consider eq(3)

The line 4x + 3y = 60 meets the x-axis at (15, 0) and y-axis at (0, 20).

And Origin(0, 0) doesnot satisfy the inequation 4x + 3y ≥ 60.

So, the section containing the origin will represent the solution set of inequation4x + 3y ≥ 60.

Clearly, x ≥ 0 and y ≥ 0 represent the first quadrant.

Hence, the solution set to the inequilities is the intersection of the above three solutions.

Thus, the shaded region represents the solution set of the given set of inequalities.

问题 6(iv) 以图形方式求解以下不等式系统：

5x + y ≥ 10、2x + 2y ≥ 12、x + 4y ≥ 12、x ≥ 0 和 y ≥ 0。

解决方案：

Let us convert the given inequations to equations.

5x + y = 10                        -(1)

2x + 2y = 12                     -(2)

x + 4y = 12                       -(3)

x = 0 and y = 0                 -(4)

Let us consider eq(1)

The line 5x + y = 10 meets the x-axis at (2, 0) and y-axis at (0, 10).

And Origin(0, 0) doesnot satisfy the inequation 5x + y ≥ 10.

So, the section containing the origin will represent the solution set of inequation 5x + y ≥ 10.

Let us consider eq(2)

The line 2x + 2y = 12 meets the x-axis at (6, 0) and y-axis at (0, 6).

And Origin(0, 0) doesnot satisfy the inequation 2x + 2y ≥ 12.

So, the section containing the origin will represent the solution set of inequation 2x + 2y ≥ 12.

Let us consider eq(3)

The line x + 4y = 12 meets the x-axis at (12, 0) and y-axis at (0, 3).

And Origin(0, 0) doesnot satisfy the inequation x + 4y ≥ 12.

So, the section containing the origin will represent the solution set of inequationx + 4y ≥ 12.

Clearly, x ≥ 0 and y ≥ 0 represent the first quadrant.

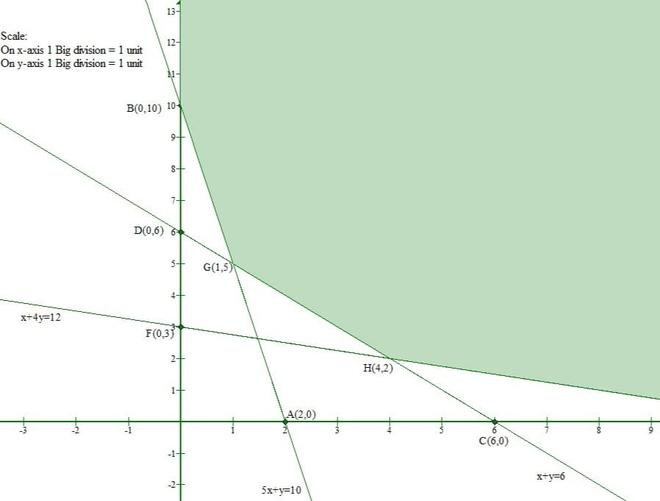
Hence, the solution set to the inequilities is the intersection of the above three solutions.

Thus, the shaded region represents the solution set of the given set of inequalities.

问题 7. 证明下列线性方程组没有解

x + 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1

解决方案：

Let us convert the given inequations to equations.

x + 2y = 3                        -(1)

3x + 4y = 12                     -(2)

x = 0 and y = 1                 -(3)

The points satisfying the eq(1) are 

x	3	0	5
y	0	1.5	-1

The points satisfying the eq(2) are

x	0	4	8
y	3	0	-3

Now, let us draw the graph representing the given inequations

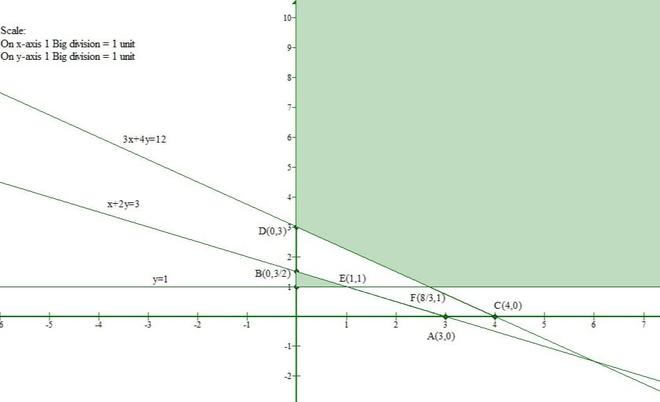
So, from the above graph we can observe that there is no common region.

Hence we can say that, the solution set of these inequalities has no solution.

问题 8. 证明下列线性不等式系统的解集是一个无界区域：

2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0

解决方案：

Given that

2x + y ≥ 8                     -(1)

x + 2y ≥ 10                  -(2)

x ≥ 0                          -(3)

y ≥ 0                           -(4)

The points satisfying the line 2x + y = 8  are 

x	0	4	2
y	8	0	4

The points satisfying the x + 2y = 10 are 

x	0	10	2
y	5	0	4

Clearly, x ≥ 0 and y ≥ 0 represent the first quadrant.

Let us draw the graph representing the given inequations

Since the common shaded region is the solution set of given set of inequilities.

Hence we proved that solution set of given linear inequations is an unbounded region.