第 11 类 RD Sharma 解决方案 – 第 33 章概率 – 练习 33.2

问题1：抛硬币。找出基本事件的总数以及与随机实验相关的事件总数。

解决方案：

Given: 

A coin is tossed.

When a coin is tossed, there will be two possible outcomes, that is Head (H) and Tail (T).

Since, the number of elementary events is 2-{H, T}

as we know that, if there are ‘n’ elements in a set, then the number of total element in its subset is 2n.

So, the total number of the experiment is 4,

There are 4 subset of S = {H}, {T}, {H, T} and Փ

Therefore,

There are total 4 events in a given experiment.

问题 2：列出与掷两个硬币的随机实验相关的所有事件。其中有多少是基本事件？

解决方案：

Given: 

Two coins are tossed once.

As we know that, when two coins are tossed then the number of possible outcomes are 2² = 4

So, 

The Sample spaces are {HH, HT, TT, TH}

Therefore, 

There are total 4 events associated with the given experiment.

问题 3：一次抛三枚硬币。描述与此随机实验相关的以下事件：

A = 获得三个正面，B = 获得两个正面和一个反面，C = 获得三个反面，D = 在第一个硬币上获得正面。

(i) 哪对事件是互斥的？

(ii) 哪些事件是基本事件？

(iii) 哪些事件是复合事件？

解决方案：

Given: 

There are three coins tossed once.

When three coins are tossed, then the sample spaces are:

S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}

So, as the question says,

A = {HHH}

B = {HHT, HTH, THH}

C = {TTT}

D = {HHH, HHT, HTH, HTT}

Now, 

A⋂ B = Փ,

A ⋂ C = Փ,

A ⋂ D = {HHH}

B ⋂ C = Փ,

B ⋂ D = {HHT, HTH}

C ⋂ D = Փ

As we know that, if the intersection of two sets are null or empty it means both the sets are Mutually Exclusive.

(i) Events A and B, Events A and C, Events B and C and events C and D are mutually exclusive.

(ii) Now, as we know that, if an event has only one sample point of a sample space, then it is called elementary events.

Thus, A and C are elementary events.

(iii) If there is an event that has more than one sample point of a sample space, it is called a compound event.

Since, B ⋂ D = {HHT, HTH}

Thus, B and D are compound events.

问题 4：在一次掷骰中描述以下事件：

(i) A = 得到一个小于 7 的数

(ii) B = 得到一个大于 7 的数

(iii) C = 获得 3 的倍数

(iv) D = 得到一个小于 4 的数

(v) E = 得到一个大于 4 的偶数。

(vi) F = 得到一个不小于 3 的数。

另外，求 A ∪ B、A ∩ B、B ∩ C、E ∩ F、D ∩ F 和$<strong>\overline F</strong>$

解决方案：

Given: 

A dice is thrown once.

Now, find the given events, and also find A ∪ B, A ∩ B, B ∩ C, E ∩ F, D ∩ F and $\overline F$

S = {1, 2, 3, 4, 5, 6}

According to the question, we have certain events as:

(i) A = Getting a number below 7

Thus, the sample spaces for A are:

A = {1, 2, 3, 4, 5, 6}

(ii) B = Getting a number greater than 7

Thus, the sample spaces for B are:

B = {Փ}

(iii) C = Getting multiple of 3

Thus, the Sample space of C is

C = {3, 6}

(iv) D = Getting a number less than 4

Thus, the sample space for D is

D = {1, 2, 3}

(v) E = Getting an even number greater than 4.

Thus, the sample space for E is

E = {6}

(vi) F = Getting a number not less than 3.

Thus, the sample space for F is

F = {3, 4, 5, 6}

Here,

A = {1, 2, 3, 4, 5, 6} and B = {Փ}

A ⋃ B = {1, 2, 3, 4, 5, 6}

A = {1, 2, 3, 4, 5, 6} and B = {Փ}

A ⋂ B = {Փ}

B = {Փ} and C = {3, 6}

B ⋂ C = {Փ}

F = {3, 4, 5, 6} and E = {6}

E ⋂ F = {6}

E = {6} and D = {1, 2, 3}

D ⋂ F = {3}

$and, for \overline F = S - F\\S= \{1,2,3,4,5,6\} and F =\{3,4,5,6\}\\\overline F = \{1,2\}\\Therefore,\\These\ are\ the\ events\ for\ given\ experiment.$

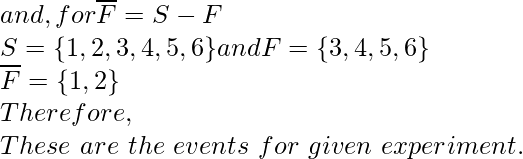
问题5：投掷了三枚硬币。描述

(i) 两个相互排斥的事件 A 和 B。

(ii) 三个事件 A、B 和 C，它们是互斥且详尽的。

(iii) 两个不互斥的事件 A 和 B。

(iv) 两个事件 A 和 B 是互斥的但不是穷尽的。

解决方案：

Given: 

Three coins are tossed.

When three coins are tossed, then the sample spaces are

S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}

Here, 

(i) The two events which are mutually exclusive are when,

A: getting no tails

B: getting no heads

Then, 

A = {HHH} and B = {TTT}

So, the intersection of this set will be null. Or, the sets are disjoint.

(ii) Three events which are mutually exclusive and exhaustive are:

A: getting no heads

B: getting exactly one head

C: getting at least two head

Thus, 

A = {TTT} 

B = {TTH, THT, HTT} and, 

C = {HHH, HHT, HTH, THH}

Hence, 

A ⋃ B = B ⋂ C = C ⋂ A = Փ and

A⋃ B⋃ C = S  

(iii) The two events that are not mutually exclusive are:

A: getting three heads

B: getting at least 2 heads

So, 

A = {HHH} 

B = {HHH, HHT, HTH, THH}

Hence, A ⋂ B = {HHH} = Փ

(iv) The two events which are mutually exclusive but not exhaustive are:

A: getting exactly one head

B: getting exactly one tail

So, 

A = {HTT, THT, TTH} and B = {HHT, HTH, THH}

It is because A ⋂ B = Փ but A⋃ B ≠ S  

问题 6：掷骰子两次。每次出现在上面的数字都会被记录下来。描述以下事件：

(i) A = 两个数都是奇数。

(ii) B = 两个数都是偶数

(iii) C = 数字之和小于 6。

另外，求 A ∪ B、A ∩ B、A ∪ C、A ∩ C。哪对事件是互斥的？

解决方案：

Given: 

A dice is thrown twice. Each time number appearing on it is recorded.

When a dice is thrown twice then the number of sample spaces are 6² = 36

Here,

The possibility both odd numbers are:

A = {(1, 1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5)}

Thus, possibility of both even numbers is:

B = {(2, 2), (2, 4), (2, 6), (4, 2), (4, 4), (4, 6), (6, 2), (6, 4), (6, 6)}

And, possible outcome of sum of the numbers is less than 6.

C = {(1, 1)(1, 2)(1, 3)(1, 4)(2, 1)(2, 2)(2, 3)(3, 1)(3, 2)(4, 1)}

Hence,

(AՍB) = {(1, 1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5) (2, 2)(2, 4)(2, 6)(4, 2)(4, 4)(4, 6)(6, 2)(6, 4)(6, 6)}

(AՌB) = {Փ}

(AUC) = {(1, 1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5) (1, 2)(1, 4)(2, 1)(2, 2)(2, 3)(3, 1)(3, 2)(4, 1)}

(AՌC) = {(1, 1), (1, 3), (3, 1)}

Therefore,

(AՌB) = Փ and (AՌC) ≠ Փ, A and B are mutually exclusive, but A and C are not.

问题 7：掷了两个骰子。事件 A、B、C、D、E和 F 描述如下：

A=在第一个骰子上获得偶数。

B=在第一个骰子上得到一个奇数。

C=两个骰子上的数字之和最多为 5。

D=得到骰子上大于5但小于10的数字之和。

E=得到至少 10 作为骰子上数字的总和。

F=在其中一个骰子上得到一个奇数。

(i) 描述以下事件：

A 和 B、B 或 C、B 和 C、A 和 E、A 或 F、A 和 F

(ii) 说明真假：

(a) A 和 B 互斥

(b) A 和 B 是相互排斥和详尽的事件。

(c) A 和 C 是互斥事件。

(d) C 和 D 是相互排斥和详尽的事件。

(e) C、D和 E 是互斥且详尽的事件。

(f) A' 和 B' 是互斥事件。

(g) A、B、F 是互斥且详尽的事件。

解决方案：

A = Getting an even number on the first die.

A = {(2, 1), (2, 2) (2, 3), (2, 4), (2, 5), (2, 6),

(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),

(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}    

B = Getting an odd number on the first die.

B = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),

(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),

(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}

C = Getting at most 5 as sum of the numbers on the two dice.

C = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (4, 1)}

D = Getting the sum of the numbers on the dice > 5 but < 10.

D = {(1, 5) (1, 6), (2, 4), (2, 5), (2, 6), (3, 3), (3, 5), (3, 6), (4, 2), (4, 3), (4, 4), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (6, 1), (6, 2), (6, 3)}

F = Getting an odd number on one of the dice.

F = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),

(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),

(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),

(2, 1), (2, 3), (2, 5), (4, 1), (4, 3), (4, 5), (6, 1), (6, 3), (6, 5)}

Its clear that A and B are mutually exclusive events and A ∩ B = ∅

B ∪ C = {(1, 1), (1,2), (1, 3), (1, 4), (1, 5), (1, 6), (3, 1), (3, 2), (3,3), (3, 4), (3, 6), (5, 1), (5, 2), (5, 3), (5, 5), (5, 6), (2,1), (2,2), (2, 3), (4, 1)}

B ∩ C = {(1, 1), (1, 2), (1, 3), (1, 4), (3, 1), (3, 2)}

A ∩ E = {(4, 6), (6, 4), (6, 5), (6, 6)}

A ∪ F = {(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (4, 1), (4, 2), (4, 3), (4, 4), (5, 5), (4, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)

(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)

(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)

(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}

A ∩ F = {(2, 1), (2,3), (2,5), (4,1), (4, 3), (4, 5), (6, 1), (6, 3), (6, 5)}

(ii)

a) True, A ∩ B = ∅

b) True, A ∩ B = ∅ and A ∪ B = S

c) False, A ∩ C ≠ ∅

d) False, A ∩ B = ∅ and A ∪ B ≠ S

e) True, C ∩ D = D ∩ E = C ∩ E = Φ and C ∪ D ∪ E = S

f) True, A’ ∩ B’ = ∅

g) False, A ∩ F ≠ ∅

问题 8：数字 1、2、3和 4 分别写在四张纸上。然后将纸条放入盒子中并彻底混合。一个人从盒子里抽出两张纸条，一张接一张，没有更换。描述以下事件：

A=第一张纸条上的数字大于第二张纸条上的数字。

B =第二张纸条上的数字大于2

C=两张纸条上的数字之和是6或7

D=第二张纸条上的数字是第一张纸条上的两倍。

哪对事件是互斥的？

解决方案：

We have four slips of paper with numbers 1, 2, 3 & 4.

A person draws two slips without replacement.

∴ Number of elementary events = ⁴C₂

$n(s)=\frac{4\times3}{2\times1}=6$

A = The number on the first slip is larger than the one on the second slip

A = {(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3)}

B = The number on the second slip is greater than 2

Therefore, 

B = {(1,3), (2,3) , (1,4), (2, 4), (3, 4), (4,3)}

C = The sum of the numbers on the two slips is 6 or 7

Therefore, 

C = {(2, 4), (3, 4), (4, 2), (4, 3)}

and,

D = The number on the second slips is twice that on the first slip

D = {(1, 2), (2, 4)}

and, A and D form a pair of mutually exclusive events as A ∩ B = ∅

问题 9：从一副 52 张扑克牌中取出一张牌。

(i) 实验的样本空间是多少？

(ii) 选择的牌是 A 面牌是什么情况？

解决方案：

(i) Sample space for picking up a card from a set of 52 cards is set of 52 cards itself.

(ii) For an event of chosen card be black faced card, event is a set of jack, king, queen of spades and clubs,