第 12 类 RD Sharma 解决方案 - 第 33 章二项分布 - 练习 33.1 |设置 3

问题 37. 实验成功的频率是失败的两倍。找出在接下来的 6 次试验中至少有 4 次成功的概率。

解决方案：

Let us consider X be the number of successes out of 6 experiment. Also, p denotes the probability of success and q denotes the probability of failure.

According to the question, successes are twice failures.

So,  p = 2q

Also, p + q = 1

=> 3q = 1

=> q = 1/3

And p = 1 – 1/3 = 2/3

So, the binomial distribution(n) = 6

Hence, the probability of getting r success is,

P(X = r) = $^{6}{}{C}_r \left( \frac{2}{3} \right)^r \left( \frac{1}{3} \right)^{6 - r}$, r = 0, 1, 2 . . . . . 6

P(at least 4 successes) = P(X > 4)

= P(X = 4) + P(X = 5) + P(X = 6)

= $^{6}{}{C}_4 \left( \frac{2}{3} \right)^4 \left( \frac{1}{3} \right)^{6 - 4} + ^{6}{}{C}_5 \left( \frac{2}{3} \right)^5 \left( \frac{1}{3} \right)^{6 - 5} + ^{6}{}{C}_6 \left( \frac{2}{3} \right)^6 \left( \frac{1}{3} \right)^{6 - 6}$

= $\frac{15( 2^4 ) + 6(32) + 64}{3^6}$

= $\frac{240 + 192 + 64}{729}$

= 496/729

问题 38. 一家医院有 20 台洗肾机，其中任何一台在一天内停用的机率是 0.02。确定同一天恰好有 3 台机器停止服务的概率。

解决方案：

Let us considered X be the number of machines out of service during a day. Also, p be the probability of any machine out of service during a day and q be the probability that machine will be in service on the same day.

Then, X has a binomial distribution with n = 20.

Hence, p = 0.02 and q = 0.98

Therefore, 

P(X = r) = $^{20}{}{C}_r \left( 0 . 02 \right)^r \left( 0 . 98 \right)^{20 - r}$, r = 0, 1, 2 . . . . . 20

The probability of exactly 3 machines will be out of the service on the same day is

P(X = 3) = $^{20}{}{C}_3 \left( 0 . 02 \right)^3 \left( 0 . 98 \right)^{20 - 3}$

= 1140 (0.000008) (0.7093)

= 0.006469

问题 39. 一个学生进入大学毕业的概率是 0.4。

(i) 找出该大学 3 名学生中没有人毕业的概率。

解决方案：

Let us consider X denotes the number of students that graduate from among 3 students. Also, p denotes the probability that a student entering a university will graduate.

Here, n = 3, p = 0.4 and q = 0.6

Hence, 

P(X = r) = $^{3}{}{C}_r \left( 0 . 4 \right)^r \left( 0 . 6 \right)^{3 - r}$ , r = 0, 1, 2, 3

So, the probability that none of the student will graduate is 

P(X = 0) = q³ 

= (0.6)³

= 0.216

(ii) 求该大学 3 名学生中只有 1 名毕业的概率。

解决方案：

Let us consider X denotes the number of students that graduate from among 3 students. Also, p denotes the probability that a student entering a university will graduate.

Here , n = 3, p = 0.4 and q = 0.6.

Hence, 

P(X = r) = $^{3}{}{C}_r \left( 0 . 4 \right)^r \left( 0 . 6 \right)^{3 - r}$ , r = 0, 1, 2, 3

So, the probability that only one student will graduate is 

P(X = 1) = 3 (0.4) (0.36) 

= 0.432

(iii) 求该大学 3 名学生全部毕业的概率。

解决方案：

Let us consider X denotes the number of students that graduate from among 3 students. Also, p be the probability that a student entering a university will graduate.

Here, n =3, p = 0.4 and q = 0.6

Hence, 

P(X = r) = $^{3}{}{C}_r \left( 0 . 4 \right)^r \left( 0 . 6 \right)^{3 - r}$, r = 0, 1, 2, 3

So, the probability that all the students will graduate is 

P(X = 3) = p³ 

= (0.4)³

= 0.064

问题 40. 从含有 10% 缺陷鸡蛋的批次中连续抽取 10 个鸡蛋并替换。找出至少有一个有缺陷的鸡蛋的概率。

解决方案：

Let us consider X denotes the number of defective eggs drawn from 10 eggs. Also, p denotes the probability that a drawn egg is defective.

Then, X has a binomial distribution with n = 10. 

=> p = 10% = 10/100 = 1/10

And q = 1 – p = 9/10

Hence, 

P(X = r) = $^{10}{}{C}_r \left( \frac{1}{10} \right)^r \left( \frac{9}{10} \right)^{10 - r}$ , r = 0, 1, 2 . . . . 10

So, the probability of t least one defective egg is 

= P(X > 1) = 1 – P(X = 0)

= $1 - ^{10}{}{C}_0 \left( \frac{1}{10} \right)^0 \left( \frac{9}{10} \right)^{10 - 0}$

= 1 – (9/10)¹⁰

问题 41。在 20 题的真假测验中，假设一个学生掷一枚公平的硬币来确定他对每个问题的答案。对于每一个头，他都回答“真”，对于每一个尾巴，他都回答“假”。求他正确回答至少 12 个问题的概率。

解决方案：

Let us consider X be the number of correct answers. Also, p denotes the probability of a correct answer and p be the probability of a correct answer.

So, 

=> p = 1/2

So q = 1 – 1/2 = 1/2

Then, X has a binomial distribution with n = 20.

Hence, 

P(X = r) = $^{20}{}{C}_r \left( \frac{1}{2} \right)^r \left( \frac{1}{2} \right)^{20 - r}$ , r = 0, 1, 2, 3 . . . . . . 20

= $\frac{^{20}{}{C}_r}{2^{20}}$

So, the probability that the student answers at least 12 questions correctly is

P(X > 12) = P(X = 12) + P(X = 13) + . . . + P(X = 20)

= $\frac{^{20}{}{C}_{12} + ^{20}{}{C}_{13} + . . . +^{20}{}{C}_{20}}{2^{20}}$

问题 42。假设 X 具有 n = 6 和 p = 1/2 的二项分布。证明 X = 3 是最可能的结果。

解决方案：

According to the question, x has a binomial distribution with n = 6 and p = 1/2.

So, q = 1 – p = 1 – 1/2 = 1/2

Hence, 

P(X = r) = $^{6}{}{C}_r \left( \frac{1}{2} \right)^r \left( \frac{1}{2} \right)^{6 - r}$ , r = 0, 1, 2, 3, 4, 5, 6

= ⁶C_r (1/2)⁶

=> P(X = r) = ⁶C_r (1/2)⁶

Now, by substituting r = 0, 1, 2, 3, 4, 5 and 6, we get 

P(X = 0) = ⁶C₀ (1/2)⁶

= 1/64

P(X = r) = ⁶C₁ (1/2)⁶ 

= 6/64

P(X = r) = ⁶C₂ (1/2)⁶

= 15/64

P(X = r) = ⁶C₃ (1/2)⁶

= 20/64

P(X = r) = ⁶C₄ (1/2)⁶

= 15/64

P(X = r) = ⁶C₅ (1/2)⁶

= 6/64

P(X = r) = ⁶C₆ (1/2)⁶

= 1/64

So, the tabular form is:

X	0	1	2	3	4	5	6
P(X)	1/64	6/64	15/64	20/64	15/64	6/64	1/64

Now, on comparing the probabilities, we get that X = 3 is the most likely outcome as P(X = 3) has the greatest value.

Hence proved.

问题 43. 在选择题考试中，五个问题中的每个问题只有一个是正确的，有三个可能的答案，考生仅仅通过猜测得到四个或更多正确答案的概率是多少？

解决方案：

Let us consider X denotes the number of right answers in the 5 questions. Also, p denotes the probability of guessing right answer and q denotes the probability of guessing wrong answer.

Here X can take values 0, 1, 2, 3, 4 and 5. So, X has a binomial distribution with n = 5.

Here p = 1/3

And q = 2/3

Hence, 

P(X = r) = $^{5}{}{C}_r \left( \frac{1}{3} \right)^r \left( \frac{2}{3} \right)^{5 - r}$ , r = 0, 1, 2, . . . 5

So, the probability that the student guesses 4 or more correct answers

P(X > 4) = P(X = 4) + P(X = 5)

= $^{5}{}{C}_4 \left( \frac{1}{3} \right)^4 \left( \frac{2}{3} \right)^1 + ^{5}{}{C}_5 \left( \frac{1}{3} \right)^5 \left( \frac{2}{3} \right)^0$

= $\frac{10 + 1}{3^5}$

= 11/243

问题 44. 一个人在 50 次彩票中购买了一张彩票，每张彩票中奖的机会为 1/100。

(i) 他至少中奖一次的概率是多少。

解决方案：

Let us consider X be the number of times the person wins the lottery. Also, p denotes the probability of winning a prize.

Then, X has a binomial distribution with n = 50.

=> p = 1/100

And q = 1 – 1/100 = 99/100

Hence, 

P(X = r) = $^{50}{}{C}_r \left( \frac{1}{100} \right)^r \left( \frac{99}{100} \right)^{50 - r}$ , r = 0, 1, 2 . . . 50

So, the probability of winning at least once is 

P(X > 0) = 1 – P(X – 0)

= 1 – (99/100)⁵⁰

(ii) 他恰好中奖一次的概率是多少。

解决方案：

Let us consider X be the number of times the person wins the lottery. Also, p denotes the probability of winning a prize.

Then, X has a binomial distribution with n = 50.

=> p = 1/100

And q = 1 – 1/100 = 99/100

Hence, 

P(X = r) = $^{50}{}{C}_r \left( \frac{1}{100} \right)^r \left( \frac{99}{100} \right)^{50 - r}$, r = 0, 1, 2 . . . 50

So the probability of winning at least twice is 

P(X > 2) = 1 – P(X = 0) – P(X = 1)

= $1 - \left( \frac{99}{100} \right)^{50} - ^{50}{}{C}_1 \times \frac{1}{100} \times \left( \frac{99}{100} \right)^{49}$

= $1 - \frac{{99}^{49} \times 149}{{100}^{50}}$

(iii) 他至少两次中奖的概率是多少。

解决方案：

Let us consider X be the number of times the person wins the lottery. Also, p be the probability of winning a prize.

Then, X has a binomial distribution with n = 50.

=> p = 1/100

And q = 1 – 1/100 = 99/100

Hence, 

P(X = r) = $^{50}{}{C}_r \left( \frac{1}{100} \right)^r \left( \frac{99}{100} \right)^{50 - r}$, r = 0, 1, 2 . . . 50

So, the probability of winning at least twice is 

P(X > 2) = 1 – P(X = 0) – P(X = 1)

= $1 - \left( \frac{99}{100} \right)^{50} - ^{50}{}{C}_1 \times \frac{1}{100} \times \left( \frac{99}{100} \right)^{49}$

= $1 - \frac{{99}^{49} \times 149}{{100}^{50}}$

问题 45. 射手击中目标的概率是 3/4。他/她必须至少射击多少次才能使至少击中目标一次的概率大于 0.99？

解决方案：

Let us consider the shooter fire n times and X be the number of times the shooter hits the target.

Then, X has a binomial distribution with p = 3/4 and q = 1/4 such that,

Hence, 

P(X = r) = $^{n}{}{C}_r \left( \frac{3}{4} \right)^r \left( \frac{1}{4} \right)^{n - r}$

P(X = r) = $^{n}{}{C}_r \frac{3^r}{4^n}$

Given that P (X > 1) > 0.99

=> 1 – P(X = 0) > 0.99

=> 1 – 1/4ⁿ > 0.99

=> 1/4ⁿ < 0.01

=> 4ⁿ > 1/0.01

=> 4ⁿ > 100

So, the shooter must fire at least 4 times.

问题 46. 一个人必须掷多少次公平的硬币才能使至少有一个正面的概率超过 90%？

解决方案：

Let us considered the man tosses a fair coin n times and X be the number of heads in n tosses.

As p = 1/2 and q = 1/2, 

So, 

P(X = r) = $^{n}{}{C}_r \left( \frac{1}{2} \right)^r \left( \frac{1}{2} \right)^{n - r}$ , r = 0, 1, 2, 3 . . . . n

It is given that P(X > 1) > 0.9

=> 1 – P(X = 0) > 0.9

=> $1 - ^{n}{}{C}_0 \left( \frac{1}{2} \right)^n > 0 . 9$

=>(1/2ⁿ) < 1/10

=> 2^n > 10

=> n = 4, 5, 6 . . . . 

So, the man must toss the coin at least 4 times.

问题 47. 一个人必须投掷一枚公平的硬币多少次才能使至少有一个正面的概率超过 80%？

解决方案：

Let us consider X denotes the number of heads and n be the minimum number of times that a man must toss a fair coin. 

So that probability of X ≥ 1 is more than 80 %.

Here X has a binomial distribution with p = 1/2 and q = 1/2.

P(X = r) = ⁿC_r (1/2)ⁿ

We have P(X > 1) = 1 – P(X = 0) 

= $1 - ^{n}{}{C}_0 \left( \frac{1}{2} \right)^n$

= 1 – (1/2)ⁿ

And for P(X > 1) > 80%

=> 1 – 1/2ⁿ > 0.80  

=> (1/2ⁿ) < 1 – 0.80 = 0.20

=> 2ⁿ > 1/0.2 = 5

We know, 2² < 5 while 2³ > 5.

So we get n = 3.

So, the man must toss the coin at least 3 times.

问题 48. 一对骰子被掷了 4 次。如果获得双峰被认为是成功的，请找出成功次数的概率分布。

解决方案：

Let us consider p be the probability of getting a doublet in a single throw of a pair of dice. Also, X be the number of getting doublets in 4 throws of a pair of dice. 

So, p = 6/36 = 1/6

And q = 1 – p = 1 – 1/6 = 5/6

Then, X has a binomial distribution with n = 4.

Hence, the probability of getting r doublets

P(X = r) = $^{4}{}{C}_r (\frac{1}{6} )^r (\frac{5}{6} )^{4 - r}$, r = 0, 1, 2, 3, 4

If X = 0, then P(X = 0) = $^{4}{}{C}_0 (\frac{1}{6} )^0 (\frac{5}{6} )^{4 - 0}$

=> P = (5/6)⁴

When X = 1, then P = $^{4}{}{C}_1 \left( \frac{1}{6} \right)^1 \left( \frac{5}{6} \right)^{4 - 1}$

= $\frac{2}{3} \left( \frac{5}{6} \right)^3$

When X = 2, then P = $^{4}{}{C}_2 \left( \frac{1}{6} \right)^2 \left( \frac{5}{6} \right)^{4 - 2}$

= $\frac{1}{6} \left( \frac{5}{6} \right)^2$

When X = 3, then P = $^{4}{}{C}_3 \left( \frac{1}{6} \right)^3 \left( \frac{5}{6} \right)^{4 - 3}$

= $\frac{10}{3} \left( \frac{1}{6} \right)^3$

When X = 4, then P = $^{4}{}{C}_4 (\frac{1}{6} )^4 (\frac{5}{6} )^{4 - 4}$

= (1/6)⁴

= 1/1296

问题 49. 从包含 6 个有缺陷的灯泡的 30 个灯泡中，随机抽取 4 个灯泡的样本进行更换。求缺陷灯泡数量的概率分布。

解决方案：

Let us considered X be the number of defective bulbs in a sample of 4 bulbs drawn successively with replacement.

Then, X has a binomial distribution with n = 4.

Here, p = 6/30 = 1/5

And q = 1 – 1/5 = 4/5

Then, 

P(X = r) = $^{4}{}{C}_r \left( \frac{1}{5} \right)^r \left( \frac{4}{5} \right)^{4 - r}$ , r = 0, 1, 2, 3, 4

P(X = 0) = (4/5)⁴

= 256/625

P(X = 1) = $4\left( \frac{1}{5} \right)^1 \left( \frac{4}{5} \right)^3$

= 256/625

P(X = 2) = $6 \left( \frac{1}{5} \right)^2 \left( \frac{4}{5} \right)^2$

= 96/625

P(X = 3) = $4 \left( \frac{1}{5} \right)^3 \left( \frac{4}{5} \right)^1$

= 16/625

P(X = 4) = (1/5)⁴

= 1/625

X	0	1	2	3	4
P(X)	256/625	256/625	96/625	16/625	1/625

问题 50. 求在 10 次公平骰子中，至少有 8 次掷出的分数是 3 的倍数的概率。

解决方案：

Let us consider p be the probability of getting a success and q be the probability of getting a failure. Also, X be the number of success in a sample of 10 trials.

p = 2/6 = 1/3

So, q = 1 – p 

= 1 – 1/3

= 2/3

Then X has a binomial distribution with n = 10, p = 1/3 and q = 2/3.

P(X = r) = $^{10}{}{C}_r p^r q^{10 - r}$

= $^{10}{C}_r \left( \frac{1}{3} \right)^r \left( \frac{2}{3} \right)^{\left( 10 - r \right)}$, r = 0, 1, 2, . . . , 10

So, the required probability is 

P(X > 8) = P(X = 8) + P(X = 9) + P(X = 10)

= $\frac{^{10}{}{C}_8 2^{\left( 10 - 8 \right)}}{3^{10}} + \frac{^{10}{}{C}_9 2^{\left( 10 - 9 \right)}}{3^{10}} + \frac{^{10}{C}_{10} 2^{\left( 10 - 10 \right)}}{3^{10}}$

= $\frac{45 \times 2^2}{3^{10}} + \frac{10 \times 2}{3^{10}} + \frac{1}{3^{10}}$

= $\frac{180 + 20 + 1}{3^{10}}$

= 201/3¹⁰

问题 51. 掷骰子 5 次。求奇数恰好出现 3 次的概率。

解决方案：

Let us consider p be the probability of getting an odd number in a trial. Also, X be the number of success in a sample of 5 trials.

So, p = 3/6 = 1/2

Also, q = 1 – p = 1 – 1/2 = 1/2

Then, X has binomial distribution with n = 5 and p = q = 1/2.

P(X = r) = $^{5}{}{C}_r p^r q^{\left( 5 - r \right)}$

= $^{5}{}{C}_r \left( \frac{1}{2} \right)^r \left( \frac{1}{2} \right)^{\left( 5 - r \right) }$

= ⁵C₃ (1/2)⁵ , where r = 0, 1, 2, 3, 4, 5

So, the probability that an odd number will come up exactly three times. 

P(X = 3) = ⁵C₃ (1/2)⁵

= 10/32

= 5/16

问题 52。一个人击中目标的概率是 0.25。他射门7次。他至少击中两次的概率是多少？

解决方案：

Let us consider p be the probability of hitting the target. Also, X be the number of success in a sample of 7 trial.

So, p = = 0.25 = 1/4

Also q = 1 – p = 1 – 1/4 = 3/4

Then, X has a binomial distribution with parameters n = 7 and p = 1/4.

P(X = r) = $^{7}{}{C}_r p^r q^{\left( 7 - r \right)}$

= $^{7}{}{C}_r \left( \frac{1}{4} \right)^r \left( \frac{3}{4} \right)^{\left( 7 - r \right)}$

= $\frac{^{7}{}{C}_r 3^{\left( 7 - r \right)}}{4^7}$, where r  = 0, 1, 2, 3, 4, 5

So, the probability of his hitting at least twice is

P(X > 2) = 1 – [P(X = 0) + P(X = 1)]

= $1 - \left[ \frac{^{7}{}{C}_0 3^7}{4^7} + \frac{^{7}{}{C}_1 3^6}{4^7} \right]$

= 1 – [2187/16384 + 5103/16384]

= 1 – 7290/16384

= 9094/16384

= 4547/8192

问题 53. 一家工厂生产灯泡。一个灯泡有缺陷的概率是 1/50，它们被包装在 10 个一盒中。从一个盒子中，找到概率：

(i) 没有一个灯泡有缺陷。

解决方案：

Let us consider p be the probability of getting a defective bulb. Also, X be the number of success in a sample of 10 trials.

Here p = 1/50

Also, q = 1 – p = 1 – 1/50 = 49/50

Then, X has a binomial distribution with n = 10 and p = 1/50

P(X = r) = $^{10}{}{C}_r p^r q^{\left( 10 - r \right)}$

= $^{10}{}{C}_r \left( \frac{1}{50} \right)^r \left( \frac{49}{50} \right)^{\left( 10 - r \right)}$

= $\frac{^{10}{}{C}_r {49}^{\left( 10 - r \right)}}{{50}^{10}}$, where r = 0, 1, 2, 3, . . . , 10

So, the probability that none of the bulb is defective

= P(X = 0) = $\frac{^{10}{}{C}_0 {49}^{10}}{{50}^{10}}$

= 49¹⁰/50¹⁰

(ii) 恰好有两个灯泡有缺陷。

解决方案：

Let us consider p be the probability of getting a defective bulb. Also, X be the number of success in a sample of 10 trials.

Here p  = 1/50

Also, q = 1 – p = 1 – 1/50 = 49/50

Then, X has a binomial distribution with n = 10 and p = 1/50

P(X = r) = $^{10}{}{C}_r p^r q^{\left( 10 - r \right)}$

= $^{10}{}{C}_r \left( \frac{1}{50} \right)^r \left( \frac{49}{50} \right)^{\left( 10 - r \right)}$

= $\frac{^{10}{}{C}_r {49}^{\left( 10 - r \right)}}{{50}^{10}}$, where r = 0, 1, 2, 3, . . . , 10

So, the probability that exactly two bulbs are defective

P(X = 2) = $\frac{^{10}{}{C}_2 {49}^8}{{50}^{10}}$

= $\frac{45 \times {49}^8}{{50}^{10}}$

(iii) 超过 8 个灯泡正常工作。

解决方案：

Let us consider p be the probability of getting a defective bulb. Also, X be the number of success in a sample of 10 trials.

Here p = 1/50

Also, q = 1 – p = 1 – 1/50 = 49/50

Then, X has a binomial distribution with n = 10 and p = 1/50

P(X = r) = $^{10}{}{C}_r p^r q^{\left( 10 - r \right)}$

= $^{10}{}{C}_r \left( \frac{1}{50} \right)^r \left( \frac{49}{50} \right)^{\left( 10 - r \right)}$

= $\frac{^{10}{}{C}_r {49}^{\left( 10 - r \right)}}{{50}^{10}}$, where r = 0, 1, 2, 3, . . . , 10

So, the probability that more than 8 bulbs work properly is

= P(X < 0)

= P(X = 0) + P(X = 1)

= $\frac{^{10}{}{C}_0 {49}^{10}}{{50}^{10}} + \frac{^{10}{}{C}_1 {49}^9}{{50}^{10}}$

= $\frac{{49}^{10}}{{50}^{10}} + \frac{10 \times {49}^9}{{50}^{10}}$

= $\frac{{49}^9}{{50}^{10}}\left( 49 + 10 \right)$

= $\frac{59\left( {49}^9 \right)}{\left( {50}^{10} \right)}$

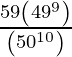
问题 54. 一个盒子有 20 支笔，其中 2 支有缺陷。计算 5 支一支笔抽出有放回的笔，最多 2 支有缺陷的概率。

解决方案：

Let us consider p be the probability of drawing a defective pen. Also, X be the number of defective pens drawn. 

Then,

=> p = 2/20 = 1/10

And q = 1 – p = 1 – 1/10 = 9/10

Then, X has a binomial distribution with n = 5

So, the probability of drawing r defective pens is

Now, P(X = r) = $^{5}{}{C}_r \left( \frac{1}{10} \right)^r \left( \frac{9}{10} \right)^{5 - r}$, r = 0, 1, 2, 3, 4, 5

So, the probability of drawing at most 2 defective pens

= P(X  ≤ 2)

= P(X = 0) + P(X = 1) + P(X = 2)

= $^{5}{}{C}_0 \left( \frac{1}{10} \right)^0 \left( \frac{9}{10} \right)^5 +^{5}{}{C}_1 \left( \frac{1}{10} \right)^1 \left( \frac{9}{10} \right)^4 + ^{5}{}{C}_2 \left( \frac{1}{10} \right)^2 \left( \frac{9}{10} \right)^3$

= $\left( \frac{9}{10} \right)^3 \left( \frac{81}{100} + 5 \times \frac{9}{100} + \frac{10}{100} \right)$

= $\frac{729}{1000} \times \frac{136}{100}$

= 0.99144