📌  相关文章
📜  第 12 类 RD Sharma 解决方案 - 第 33 章二项分布 - 练习 33.1 |设置 2

📅  最后修改于: 2022-05-13 01:54:12.660000             🧑  作者: Mango

第 12 类 RD Sharma 解决方案 - 第 33 章二项分布 - 练习 33.1 |设置 2

问题 19。一个袋子包含 7 个绿色、4 个白色和 5 个红色的球。如果四个球一个接一个地抽出来，一个是红色的概率是多少？

解决方案：

问题 20。一个袋子包含 2 个白色、3 个红色和 4 个蓝色球。从袋子里随机抽取两个球。如果 X 表示抽出的两个球中有多少个白球，描述 X 的概率分布。

解决方案：

问题 21. 一个瓮中有四个白球和三个红球。从瓮中找出三个平局中红球数量的概率分布。

解决方案：

问题 22. 求一对骰子投掷 4 次中双点数的概率分布。

解决方案：

问题 23. 求掷骰子 3 次中 6 数的概率分布。

解决方案：

问题 24. 一枚硬币被抛 5 次。如果 X 是观察到的正面数量，求 X 的概率分布。

解决方案：

问题 25. 一个无偏的骰子被掷了两次。一次成功是获得一个大于 4 的数字。求成功次数的概率分布。

解决方案：

问题 26. 抛硬币时，一个人的正面赢得卢比，反面则损失一卢比。假设他投掷一次，如果他赢了就退出，但如果他在第一次投掷时输了，他会再试一次。求该人赢得卢比数的概率分布。

解决方案：

问题 27. 五个骰子同时掷出。如果单个骰子中出现 3、4 或 5 被认为是成功的，则求至少 3 次成功的概率。

解决方案：

问题 28. 一家公司生产的产品包含 10% 的缺陷产品。证明在 8 个项目的样本中出现 2 个缺陷项目的概率是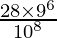\frac{28 \times 9^6}{{10}^8} .

解决方案：

问题 29. 在普通的 52 张牌中抽取一张牌并将其替换。一张牌必须抽多少次才能使

(i) 至少有一个平均的机会画一颗心

解决方案：

(ii) 画心的概率大于 3/4

解决方案：

问题 30. 数学系有 8 名研究生助理，他们被分配到同一个办公室。每个助理在家学习的可能性与在办公室学习的可能性一样。办公室必须有多少张桌子才能让每个助理至少 90% 的时间都有一张桌子？

解决方案：

问题 31. 一枚无偏的硬币被抛 8 次。通过使用二项分布，找出至少出现 6 个正面的概率。

解决方案：

问题 32. 同时抛 6 个硬币。求得到的概率：

(一) 3个头

解决方案：

(ii) 无头

解决方案：

(iii) 至少一名

解决方案：

问题 33。假设插入某种类型的设备中的无线电管工作超过 500 小时的概率为 0.2。如果我们随机测试 4 个管子，其中恰好三个管子函数超过 500 小时的概率是多少？

解决方案：

问题 34. 某种部件在给定的冲击测试中幸存下来的概率是 3/4。

(i) 找出在 5 个被测试的组件中恰好有 2 个能够存活的概率。

解决方案：

(ii) 找出在 5 个被测试的组件中最多有 3 个能够存活的概率。

解决方案：

问题 35。假设从飞机上投下的炸弹击中某个目标的概率为 0.2。如果投下 6 颗炸弹，求概率：

(i) 正好 2 击中目标。

解决方案：

(ii) 至少有 2 人会击中目标

解决方案：

问题 36. 众所周知，60% 的小鼠接种了血清后可免受某种疾病的侵害。如果接种了 5 只小鼠，求以下概率：

(i) 没有人感染这种疾病。

解决方案：

(ii) 3 人以上感染该疾病。

解决方案：