第 12 类 RD Sharma 解决方案 - 第 27 章方向余弦和方向比 - 练习 27.1

问题 1. 如果一条线分别与 x、y 和 z 轴的正方向成 90°、60°和 30°。求其方向余弦。

解决方案：

Let us considered the direction cosines of line be l, m, n.

As we know that direction cosines of a line will be cosines 

of the angle made with x, y and z axis.

l = cos90° = 0

m = cos60° = 1/2

n = cos30° = √3/2

Hence, the direction cosines of line are 0, 1/2, √3/2.

问题 2. 如果一条线的方向比为 2、-1、-2。确定其方向余弦。

解决方案：

Let us considered the direction cosines of line be l, m, n.

Given direction ratios are 2, -1, -2.

We can determine direction cosines l, m, n of a given line from direction ratios r1, r2, r3 by

l = $\frac{r1}{\sqrt{(r1)^2+(r2)^2+(r3)^2}}$

m = $\frac{r2}{\sqrt{(r1)^2+(r2)^2+(r3)^2}}$

n = $\frac{r3}{\sqrt{(r1)^2+(r2)^2+(r3)^2}}$

Here r1 = 2, r2 = -1, r3 = -2

Thus,

l = $\frac{2}{\sqrt{2^2+(-1)^2+(-2)^2}}$= 2/3

m = $\frac{-1}{\sqrt{2^2+(-1)^2+(-2)^2}}$= -1/3

n = $\frac{-2}{\sqrt{2^2+(-1)^2+(-2)^2}}$= -2/3

Hence, the direction ratios of the given line are 2/3, -1/3, -2/3.

问题 3. 求通过两点 (-2, 4, -5) 和 (1, 2, 3) 的线的方向余弦。

解决方案：

Let us considered the direction cosines of the line passing through two points A(x1, x2, x3) and B(y1, y2, y3) are 

$\frac{x2-x1}{AB}$,$\frac{y2-y1}{AB}$,$\frac{z2-z1}{AB}$

So, the distance between A and B = $\sqrt{(x2-x1)^2+(y2-y1)^2+(z2-z1)^2}$

It given that A(-2, 4, -5), and B(1, 2, 3)

AB = $\sqrt{(1-(-2))^2+(2-4)^2+(3-(-5)^2)}$

= √77

Now, the direction cosines will be $\frac{1-(-2)}{\sqrt77}$,$\frac{2-(4)}{\sqrt77}$,$\frac{3-(-5)}{\sqrt77}$

Hence, the direction cosines of the line passing through two points A and B are $\frac3{\sqrt{77}}$,$\frac{-2}{\sqrt{77}}$,$\frac8{\sqrt{77}}$

问题 4. 使用方向比表明点 A(2, 3, -4), B(1, -2, 3), C(3, 8, -11) 是共线的。

解决方案：

Given points are A(2, 3, -4), B(1, -2, 3), C(3, 8, -11)

Let us considered the direction ratios of the line joining the points (x1, y1, z1) and (x2, y2, z2) are x2 – x1, y2 – y1, z2 – z1.

So, the direction ratios of the line joining A and B are (1 – 2, -2 – 3, 3 – (-4)) i.e (-1, -5, 7)

And the direction ratios of the line joining B and C are (3 – 1, 8 – (-2), -11 – 3) i.e (2, 10, -14)

Let us assume that the direction ratios for AB be (r1, r2, r3) and BC be (r4, r5, r6)

So, the points A, B, and C said to be collinear when r1/r4 = r2/r5 = r3/r6 = constant

Here (r1, r2, r3) = (-1, -5, 7) and (r4, r5, r6) = (2, 10, -14)

Now,

r1/r4 = -1/2

r2/r5 = -5/10 = -1/2

r3/r6 = 7/-14 = -1/2

Here, $\frac{r1}{r4}=\frac{r2}{r5}=\frac{r3}{r6}=\frac{-1}2$

Hence, A(2, 3, -4), B(1, -2, 3), and C(3, 8, -11) are collinear.

问题 5. 求顶点为 (3, 5, -4), (-1, 1, 2), (-5, -5, -2) 的三角形各边的方向余弦。

解决方案：

Let us consider ABC is a triangle whose vertices are A(3, 5, -4), B(-1, 1, 2), C(-5, -5, -2).

So, the direction ratios for AB are (-1 – 3, 1 – 5, 2 – (-4)) = (-4, -4, 6)

Direction cosines for AB = $\frac{-4}{\sqrt{(-4)^2+(-4)^2+(6^2)}}$,$\frac{-4}{\sqrt{(-4)^2+(-4)^2+(6^2)}}$,$\frac{6}{\sqrt{(-4)^2+(-4)^2+(6^2)}}$

= $\frac{-4}{2\sqrt{17}}$,$\frac{-4}{2\sqrt{17}}$,$\frac{6}{2\sqrt{17}}$

= $\frac{-2}{\sqrt{17}}$,$\frac{-2}{\sqrt{17}}$,$\frac{3}{\sqrt{17}}$

Direction ratios for BC are (-5 – (-1), -5 – 1, -2 – 2) = (-4, -6, -4)

Direction cosines for BC = $\frac{-4}{\sqrt{(-4)^2+(-6)^2+(-4)^2}}$,$\frac{-6}{\sqrt{(-4)^2+(-6)^2+(-4)^2}}$,$\frac{-4}{\sqrt{(-4)^2+(-6)^2+(-4)^2}}$

= $\frac{-4}{2\sqrt{17}}$,$\frac{-6}{2\sqrt{17}}$,$\frac{-4}{2\sqrt{17}}$

= $\frac{-2}{\sqrt{17}}$,$\frac{-3}{\sqrt{17}}$,$\frac{-2}{\sqrt{17}}$

Direction ratios for CA are (-5 – 3, -5 – 5, -2 – (-4)) ⇒ (-8, -10, 2)

Direction cosines for CA = $\frac{-8}{\sqrt{(-8)^2+(-10)^2+(2)^2}}$,$\frac{-10}{\sqrt{(-8)^2+(-10)^2+(2)^2}}$,$\frac{2}{\sqrt{(-8)^2+(-10)^2+(2)^2}}$

=$\frac{-8}{2\sqrt{42}}$,$\frac{-10}{2\sqrt{42}}$,$\frac{2}{2\sqrt{42}}$

=$\frac{-4}{\sqrt{42}}$,$\frac{-5}{\sqrt{42}}$,$\frac{1}{\sqrt{42}}$

问题 6. 求方向比与 1、-2、1 和 4、3、2 成正比的向量之间的角度。

解决方案：

Let $\vec{a}$ be a vector with direction ratios 1, -2, 1

$\vec{a}$= $\hat{i}-2\hat{j}+\hat{k}$

Let $\vec{b}$ be a vector with direction ratios 4, 3, 2.

$\vec{b}$= $4\hat{i}+3\hat{j}+2\hat{k}$

Let $\theta$ be angles between vectors

cosθ = $\frac{\vec{a}.\vec{b}}{|\vec{a}||\vec{b}|}$

= $\frac{(\hat{i}-2\hat{j}+\hat{k})(4\hat{i}+3\hat{j}+2\hat{k})}{|\hat{i}-2\hat{j}+\hat{k}||4\hat{i}+3\hat{j}+2\hat{k}|}$

= $\frac{4-6+2}{\sqrt{1+4+1}{\sqrt{16+9+4}}}$

= 0

cosθ = 0 ⇒ θ = π​/2  

Hence, the angle between given vectors are π​/2.

问题 7. 求方向余弦与 2、3、-6 和 3、-4、5 成正比的向量之间的角度。

解决方案：

Let $\vec{a}$ be a vector with direction ratios 2, 3, -6

⇒ $\vec{a}=2\hat{i}+3\hat{j}-6\hat{k}$

Let $\vec{b}$ be a vector with direction ratios 3, -4, 5

⇒ $\vec{b}=3\hat{i}-4\hat{j}+5\hat{k}$

Let $\theta$ be angles between vectors

cosθ = $\frac{\vec{a}.\vec{b}}{|\vec{a}||\vec{b}|}$

=$\frac{(2\hat{i}+3\hat{j}-6\hat{k}).(3\hat{i}-4\hat{j}+5\hat{k})}{|2\hat{i}+3\hat{j}-6\hat{k}||3\hat{i}-4\hat{j}+5\hat{k}|}$

=$\frac{6-12-30}{\sqrt{4+9+36}\sqrt{9+16+25}}$

=$\frac{-36}{\sqrt{49}\sqrt{50}}$

=$\frac{-36}{35\sqrt2}$

=$\frac{-36×\sqrt2}{35×\sqrt2×\sqrt2}$

=$\frac{-18\sqrt2}{35}$

θ = $cos^{-1}(\frac{-18\sqrt2}{35})$

Hence, the angle between the given vectors is $cos^{-1}(\frac{-18\sqrt2}{35})$

问题 8. 求方向比与 2:3:6 和 1:2:2 成正比的直线之间的锐角。

解决方案：

Let $\vec{a}$ be a vector with direction ratios 2, 3, 6

⇒ $\vec{a}=2\hat{i}+3\hat{j}+6\hat{k}$

Let $\vec{b}$ be a vector with direction ratios 1, 2, 2

⇒ $\vec{b}=\hat{i}+2\hat{j}+2\hat{k}$

Let θ be angles between vectors

cos θ =$\frac{\vec{a}.\vec{b}}{|\vec{a}||\vec{b}|}$

=$\frac{(2\hat{i}+3\hat{j}+6\hat{k}).(\hat{i}+2\hat{j}+2\hat{k})}{|2\hat{i}+3\hat{j}+6\hat{k}||\hat{i}+2\hat{j}+2\hat{k}|}$

=$\frac{2+6+12}{\sqrt{4+9+36}\sqrt{1+4+4}}$

=$\frac{20}{21}$

θ = $cos^{-1}(\frac{20}{21})$

Hence, the angle between the given vectors is $cos^{-1}(\frac{20}{21})$

问题 9. 证明点 (2, 3, 4), (-1, -2, 1), (5, 8, 7) 是共线的。

解决方案：

 It is given that, A(2, 3, 4), B(-1, -2, 1), and C(5, 8, 7) are collinear,

so direction ratios of any two lines from AB, BC, CA are to be proportional.

Let us assume direction ratios for AB is (r1, r2, r3) and BC is (r4, r5, r6)

The proportionality constant can be stated as r1/r4 = r2/r5 = r3/r6 = constant

Direction ratios for AB = (-1 – 2, -2 – 3, 1 – 4) = (-3, -5, -3)

⇒ r1 = -3, r2 = -5, r3 = -3

Direction ratios for BC = (5 – (-1), 8 – (-2), 7 – 1) = (6, 10, 6)

⇒ r4 = 6, r5 = 10, r6 = 6

r1/r4 = -3/6 = -1/2

r2/r5 = -5/10 = -1/2

r3/r6 = -3/6 = -1/2

So, $\frac{r1}{r4}=\frac{r2}{r5}=\frac{r3}{r6}=\frac{-1}2$

Hence, the given points are collinear.

问题 10. 证明通过点 (4, 7, 8) 和 (2, 3, 4) 的线平行于通过点 (-1, -2, 1) 和 (1, 2, 5) 的线.

解决方案：

The given points are A(4, 7, 8), B(2, 3, 4), C(-1, -2, 1), and D(1, 2, 5)

Also, the two lines are said to be parallel if the direction ratios of two lines are proportional.

Now, let us assume direction ratios for AB is (r1, r2, r3) and CD is (r4, r5, r6)

Direction ratio for AB = (2 – 4, 3 – 7, 4 – 8)

⇒ (r1, r2, r3) = (-2,-4,-4)

⇒ r1 = -2, r2 = -4, r3 = -4

Direction ratio for CD = (1 – (-1), 2 – (-2), 5 – 1)

⇒ (r4, r5, r6) = (2, 4, 4)

⇒ r4 = 2, r5 = 4, r6 = 4

The proportionality constant can be stated as r1/r4 = r2/r5 = r3/r6 = constant

r1/r4 = -2/2 = -1

r2/r5 = -4/4 = -1

r3/r6 = -4/4 = -1

So, $\frac{r1}{r4}=\frac{r2}{r5}=\frac{r3}{r6}=-1$

Hence, the line through the points (4, 7, 8) and (2, 3, 4) is parallel to 

line through the points (-1, -2, 1) and(1, 2, 5).

问题 11. 证明通过点 (1, -1, 2) 和 (3, 4, -2) 的线垂直于通过点 (0, 3, 2) 和 (3, 5, 6) 的线.

解决方案：

The given points are A(1, -1, 2), B(3, 4, -2), C(0, 3, 2) and D(3, 5, 6)

As we know that the two lines with direction ratios (r1, r2, r3) and (r4, r5, r6) are 

perpendicular to each other if it satisfies the given condition r1.r4 + r2.r5 + r3.r6 = 0

Let us assume direction ratios for AB is (r1, r2, r3) and CD is (r4, r5, r6)

Direction ratio for AB = (3 – 1, 4 – (-1), -2 – 2)

⇒ (r1, r2, r3) = (2, 5, -4)

⇒ r1 = 2, r2 = 5, r3 = -4

Direction ratio for CD = (3 – 0, 5 – 3, 6 – 2)

⇒ (r4, r5, r6) = (3, 2, 4)

⇒ r4 = 3, r5 = 2, r6 = 4

Let us check the condition

r1.r4 + r2.r5 + r3.r6 = 2 × 3 + 5 × 2 + -4 × 4

= 6 + 10 – 16

 = 0

Here, the condition is satisfied, so AB and CD are perpendicular to each other.

Hence, the line through the points (1, -1, 2) and (3, 4, -2) is perpendicular 

to the line through the points (0, 3, 2) and (3, 5, 6).

问题 12. 证明连接原点和点 (2, 1, 1) 的线垂直于由点 (3, 5, -1) 和 (4, 3, -1) 确定的线。

解决方案：

The given points are O(0, 0, 0), A(2, 1, 1), B(3, 5, -1), and C(4, 3, -1)

As we know that the two lines with direction ratios (r1, r2, r3) and (r4, r5, r6) are 

perpendicular to each other if it satisfies the given condition r1.r4 + r2.r5 + r3.r6 = 0

Let us assume direction ratios for OA is (r1, r2, r3) and BC is (r4, r5, r6)

Direction ratios for OA = (2 – 0, 1 – 0, 1 – 0)

⇒ (r1, r2, r3) = (2, 1, 1)

⇒ r1 = 2, r2 = 1, r3 = 1

Direction ratios for BC = (4 – 3, 3 – 5, -1 – (-1))

⇒ (r4, r5, r6) = (1, -2, 0)

⇒ r4 = 1, r5 = -2, r6 = 0

Now check the condition

r1.r4 + r2.r5 + r3.r6 = 2 × 1 + 1 × -2 + 1 × 0

= 2 – 2

= 0

Here, the condition is satisfied, so OA and BC are perpendicular to each other.

Hence, the line joining the origin to the point (2, 1, 1) is perpendicular to 

line determined by the points (3, 5, -1) and (4, 3, -1).

问题 13. 求方向比与 a、b、c 和 b-c、c-a、a-b 成正比的直线之间的角度。

解决方案：

Let us assume a1 = a, b1 = b, c1 = c

and a2 = b – c, b2 = c – a, c2 = a – b

Let θ be angles between the given lines 

cosθ = $\frac{a1a2+b1b2+c1c2}{\sqrt{(a1)^2+(b1)^2+(c1)^2}\sqrt{(a2)^2+(b2)^2+(c2)^2}}$

= $\frac{a(b-c)+b(c-a)+c(a-b)}{\sqrt{a^2+b^2+c^2}\sqrt{(b-c)^2+(c-a)(a-b)}}$

= $\frac{ab-ac+bc-ab+ac-bc}{\sqrt{a^2+b^2+c^2}\sqrt{(b-c)^2+(c-a)(a-b)}}$

= 0

⇒ θ = π/2 

Hence, the angle between the given lines is 90°.

问题 14. 如果 A、B、C、D 点的坐标分别为 (1, 2, 3), (4, 5, 7), (-4, 3, -6), 和 (2, 9, 2 ）。然后求 AB 与 CD 的夹角。

解决方案：

The given points are A(1, 2, 3), B(4, 5, 7), C(-4, 3, -6), and D(2, 9, 2)

Let us assume direction ratios for AB is (r1, r2, r3) and CD is (r4, r5, r6)

Direction ratios for AB = (4 – 1, 5 – 2, 7 – 3)

⇒ (r1, r2, r3) = (3, 3, 4)

⇒ r1 = 3, r2 = 3, r3 = 4

Direction ratios for CD = (2 – (-4), 9 – 3, 2 – (-6))

⇒ (r4, r5, r6) = (6, 6, 8)

⇒ r4 = 6,r5 = 6, r6 = 8

cosθ = $\frac{r1r4+r2r5+r3r6}{\sqrt{(r1)^2+(r2)^2+(r3)^2}\sqrt{(r4)^2+(r5)^2+(r6)^2}}$

= $\frac{18+18+32}{\sqrt{9+9+16}\sqrt{36+36+64}}$

= $\frac{68}{68}$

= 1

⇒ θ = 0°

Hence, the angle between the lines AB and CD is 0°.

问题 15. 找出由关系连接的线的方向余弦：l + m + n = 0 和 2lm + 2ln – mn = 0。

解决方案：

Given that, 

l + m + n = 0           ……..(1)     

2lm + 2ln – mn = 0          ……..(2)     

From eq(1), we get 

l = -m – n

On substituting the value of eq(2), we get

⇒ 2(-m – n)m + 2(-m – n)n – mn = 0

⇒ 2(-m² – mn) + 2(-mn – n²) – mn = 0

⇒ -2m² – 2mn – 2mn – 2n² – mn = 0

⇒ -2m² – 2n² = 5mn

⇒ 2m² + 2n² + 5mn = 0

⇒ (m + 2n)(2m + n) = 0

⇒ m = -2n or m = -n/2

If m = -2n, then l = n from eq(1)

If m = -n/2, then l = -n/2 from eq(1)

So, the direction ratios of two lines proportional to (n, -2n, n) and (-n/2, -n/2, n) i.e (1, -2, 1) and (-1/2, -1/2, 1)

Now their direction cosines will be $\pm\frac1{\sqrt6},\pm\frac{-2}{\sqrt6},\pm\frac1{\sqrt6}$and $\pm\frac{-1}{\sqrt6},\pm\frac{-1}{\sqrt6},\pm\frac2{\sqrt6}$

问题 16(i)。找出方向余弦由方程 l + m + n = 0 和 l ² + m ² – n ² = 0 给出的直线之间的角度。

解决方案：

Given that,

l + m + n = 0           ……..(1)     

l² + m² – n² = 0            ……..(2)     

From eq(1), we get

l = -m – n

On substituting the value of l in eq(2), we get

⇒ (-m – n)² + m² – n² = 0

⇒ m² + n² + 2mn + m² – n² = 0

⇒ 2m² + 2mn = 0

⇒ 2m(m + n) = 0

⇒ m = 0 or m = -n

If m = 0 then l = -n from eq(1) 

If m = -n then l = 0 from eq(2) 

So, the direction ratios for first line is (-n, 0, n) 

Direction ratios for second line is (0, -n, n) 

Let $\theta$ be angles between two lines

cosθ = $\frac{a1a2+b1b2+c1c2}{\sqrt{(a1)^2+(b1)^2+(c1)^2}\sqrt{(a2)^2+(b2)^2+(c2)^2}}$

Where a1, b1, c1 are the direction ratios of first line and 

a2, b2, c2 are the direction ratios of second line

=$\frac{(-n×0)+(0×-n)+(n×n)}{\sqrt{n^2+0+n^2}\sqrt{0+(-n)^2+n^2}}$

=$\frac{n^2}{\sqrt{2n^2}\sqrt{2n^2}}$

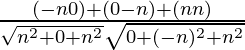
= 1/2

⇒ θ = $cos^{-1}(\frac12)$

= 60°

Hence, the angle between given two lines is 60°.

问题 16(ii)。找出方向余弦由方程 2l – m + 2n = 0 和 mn + nl + lm = 0 给出的直线之间的角度。

解决方案：

Given that,

 2l – m + 2n = 0           ……..(1)   

mn + nl + lm = 0         ……..(2)   

From eq(1), we get

m = 2l + 2n

On substituting the value of m in eq(2), we get

⇒ (2l + 2n)n + nl + l(2l + 2n) = 0

⇒ 2ln + 2n² + nl + 2l² + 2ln = 0

⇒ 2n² + 5ln + 2l² = 0

⇒ (2n + l)(n + 2l) = 0

⇒ n = -l/2 or n = -2l

If n = -l/2, then m = l

If n = -2l, then m = -2l

So, the direction ratios for first line is (l, l, -l/2)

Direction ratios for second line is (l, -2l, -2l) 

Let θ be angles between two lines

cosθ = $\frac{a1a2+b1b2+c1c2}{\sqrt{(a1)^2+(b1)^2+(c1)^2}\sqrt{(a2)^2+(b2)^2+(c2)^2}}$

Where a1, b1, c1 are the direction ratios of first line and 

a2, b2, c2 are the direction ratios of second line

= $\frac{l×l+l×-2l+\frac{-l}2×-2l}{\sqrt{l^2+l^2+\frac{l^2}4}\sqrt{l^2+(-2l)^2+(-2l)^2}}$

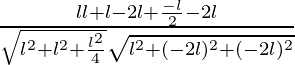
= 0°

⇒ θ = 90°

Hence, the angle between given two lines is 90°.

问题 16(iii)。找出方向余弦由方程 l + 2m + 3n = 0 和 3lm – 4ln + mn = 0 给出的直线之间的角度。

解决方案：

Given that, l + 2m + 3n = 0            ……..(1)   

3lm – 4ln + mn = 0               ……..(2)   

From eq(1), we get

l = -2m – 3n

On substituting the value of l in eq(2), we get

⇒ 3(-2m – 3n)m – 4(-2m – 3n)n + mn = 0

⇒ -6m² – 9mn + 8mn + 12n² + mn = 0

⇒ -6m² + 12n² = 0

⇒ 2n² – m² = 0

⇒ (√2n + m)(√2n – m) = 0

⇒ m = -√2n or m = √2n

If m = -√2n then l = (2√2 – 3)n

If m = √2n then l = -(2√2 + 3)n

So, the direction ratios for first line is ((2√2 – 3)n, -√2n, n)

Direction ratios for second line is (-(2√2 + 3)n, √2n, n)

Let θ be angles between two lines

cosθ = $\frac{a1a2+b1b2+c1c2}{\sqrt{(a1)^2+(b1)^2+(c1)^2}\sqrt{(a2)^2+(b2)^2+(c2)^2}}$

Where a1, b1, c1 are the direction ratios of first line and 

a2, b2, c2 are the direction ratios of second line.

= $\frac{(2\sqrt2-3)n×-(2\sqrt2+3)+(-\sqrt{2}n)×\sqrt{2}n+n×n}{\sqrt{((2\sqrt2-3)n)^2+(\sqrt2n)^2+n^2}\sqrt{(-(2\sqrt2+3)n)^2+(\sqrt2n)^2+n^2}}$

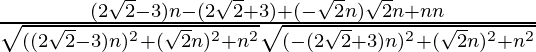
= 0

⇒ θ = 90°

Hence, the angle between given two lines is 90°.

问题 16(iv)。找出方向余弦由方程 2l + 2m – n = 0 和 mn + ln + lm = 0 给出的直线之间的角度。

解决方案：

Given that, 

2l + 2m – n = 0            ……..(1)   

mn + ln + lm = 0         ……..(2)   

From eq(1), we get

n = 2l + 2m

On substituting the value of l in eq(2), we get

⇒ m(2l + 2m) + l(2l + 2m) + lm = 0

⇒ 2lm + 2m² + 2l² + 2lm + lm = 0

⇒ 2m² + 5lm + 2l² = 0

⇒ (2m + l)(m + 2l) = 0

⇒ m = -l/2 or m = -2l

If m = -l/2 then n = l

If m = -2l then n = -2l

So, the direction ratios for first line is (l, -l/2, l)

Direction ratios for second line is (l, -2l, -2l)

Let θ be angles between two lines

cosθ = $\frac{a1a2+b1b2+c1c2}{\sqrt{(a1)^2+(b1)^2+(c1)^2}\sqrt{(a2)^2+(b2)^2+(c2)^2}}$

Where a1, b1, c1 are the direction ratios of first line and 

a2, b2, c2 are the direction ratios of second line.

=$\frac{(l×l)+(-l/2×-2l)+(l×-2l)}{\sqrt{l^2+(-l/2)^2+l^2}\sqrt{l^2+(-2l)^2+(-2l)^2}}$

=$\frac{2l^2-2l^2}{\sqrt{l^2+(-l/2)^2+l^2}\sqrt{l^2+(-2l)^2+(-2l)^2}}$

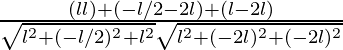
= 0

⇒ θ = 90°

Hence, the angle between given two lines is 90°.