第 12 类 RD Sharma 解决方案 – 第 17 章增加和减少函数 – 练习 17.2 |设置 3

问题 26. 找出 f(x) = log (1 + x) – x/(1 + x) 增加或减少的区间。

解决方案：

We have,

f(x) = log (1 + x) – x/(1 + x)

On differentiating both sides with respect to x, we get

f'(x) = $\frac{d}{dx}(\log(1+x) -\frac{x}{(1+x)})$

f'(x) = $\frac{1}{1+x}-\frac{(1+x)(1)-x(1)}{(1+x)^2}$

f'(x) = $\frac{1}{1+x}-\frac{1+x-x}{(1+x)^2}$

f'(x) = $\frac{1}{1+x}-\frac{1}{(1+x)^2}$

f'(x) = $\frac{1+x-1}{(1+x)^2}$

f'(x) = $\frac{x}{(1+x)^2}$

For f(x), we need to find the critical point, so we get,

=> f'(x) = 0

=> $\frac{x}{(1+x)^2}$ = 0

=> x = 0

Clearly, f'(x) > 0 if x > 0.

Also, f'(x) < 0 if –1 < x < 0 or x < –1.

Thus f(x) is increasing in (0, ∞) and decreasing in (–∞, –1) ∪ (–1, 0).

问题 27. 找出 f(x) = (x + 2)e ^–x增加或减少的区间。

解决方案：

We have,

f(x) = (x + 2)e^–x

On differentiating both sides with respect to x, we get

f'(x) = $\frac{d}{dx}((x + 2)e^{-x})$

f'(x) = e^–x – e^–x (x + 2)

f'(x) = e^–x (1 – x – 2)

f'(x) = e^–x (x + 1)

For f(x), we need to find the critical point, so we get,

=> f'(x) = 0

=> e^–x (x + 1) = 0

=> x = –1

Clearly, f'(x) > 0 if x < –1.

Also, f'(x) < 0 if x > –1.

Thus f(x) is increasing in (–∞, –1) and decreasing in (–1, ∞).

问题 28. 证明由 f(x) = 10 ^x给出的函数f 对于所有 x 都在增加。

解决方案：

We have,

f(x) = 10^x

On differentiating both sides with respect to x, we get

f'(x) = $\frac{d}{dx}(10^x)$

f'(x) = 10^x log 10

Now we have, x ∈ R, we get

=> 10^x > 0

=> 10^x log 10 > 0

=> f'(x) > 0

Thus, f(x) is increasing for all x.

Hence proved.

问题 29. 证明由 f(x) = x – [x] 给出的函数f 在 (0, 1) 中增加。

解决方案：

We have,

f(x) = x – [x]

On differentiating both sides with respect to x, we get

f'(x) = $\frac{d}{dx}(x - [x])$

f'(x) = 1

Now we have,

=> 1 > 0

=> f'(x) > 0

Thus, f(x) is increasing in the interval (0, 1).

Hence proved.

问题 30. 证明函数f(x) = 3x ⁵ + 40x ³ + 240x 在 R 上增加。

解决方案：

We have,

f(x) = 3x⁵ + 40x³ + 240x

On differentiating both sides with respect to x, we get

f'(x) = $\frac{d}{dx}(3x^5 + 40x^3 + 240x)$

f'(x) = 15x⁴ + 120x² + 240

f'(x) = 15 (x⁴ + 8x² + 16)

f'(x) = 15 (x² + 4)²

Now we know,

=> (x² + 4)² > 0

=> 15 (x² + 4)² > 0

=> f'(x) > 0

Thus, the given f(x) is increasing on R.

Hence proved.

问题 31. 证明 f(x) = log cos x 给出的函数f 在 (–π/2, 0) 上严格递增，在 (0, π/2) 上严格递减。

解决方案：

We have,

f(x) = log cos x

On differentiating both sides with respect to x, we get

f'(x) = $\frac{d}{dx}(\log \cos x)$

f'(x) = $\frac{1}{cosx}(-sinx)$

f'(x) = $\frac{-sinx}{cosx}$

f'(x) = – tan x

Now for x ∈ (0, π/2), we get

=> 0 < x < π/2

=> tan 0 < tan x < tan π/2

=> 0 < tan x < 1

=> tan x > 0

=> – tan x < 0

=> f'(x) < 0

Also for x ∈ (–π/2, 0), we have,

=> –π/2 < x < 0

=> tan (–π/2) < tan x <  tan 0

=> –1 < tan x < 0

=> tan x < 0

=> – tan x > 0

=> f'(x) > 0

Thus, f(x) is strictly increasing on the interval (–π/2, 0) and strictly decreasing on the interval (0, π/2).

Hence proved.

问题 32. 证明由 f(x) = x ³ – 3x ² + 4x 给出的函数f 在 R 上严格递增。

解决方案：

We have,

f(x) = x³ – 3x² + 4x 

On differentiating both sides with respect to x, we get

f'(x) = $\frac{d}{dx}(x^3 - 3x^2 + 4x)$

f'(x) = 3x² – 6x + 4

f'(x) = 3 (x² – 2x + 1) + 1

f'(x) = 3 (x – 1)² + 1

Now, we know,

=> (x – 1)² > 0

=> 3 (x – 1)² > 0

=> 3 (x – 1)² + 1 > 0

=> f'(x) > 0

Thus, f(x) is strictly increasing on R.

Hence proved.

问题 33. 证明由 f(x) = cos x 给出的函数f 在 (0, π) 处严格递减，在 (π, 2π) 处递增，在 (0, 2π) 处既不递增也不递减。

解决方案：

We have,

f(x) = cos x

On differentiating both sides with respect to x, we get

f'(x) = $\frac{d}{dx}(cos x)$

f'(x) = – sin x

Now for x ∈ (0, π), we get

=> 0 < x < π

=> sin 0 < sin x < sin π

=> 0 < sin x < 0

=> sin x > 0

=> – sin x < 0

=> f'(x) < 0

Also for x ∈ (π, 2π), we get

=> π < x < 2π

=> sin 0 < sin x < sin π

=> 0 < sin x < 0

=> sin x < 0

=> – sin x > 0

=> f'(x) > 0

Thus, f(x) is strictly increasing on the interval (π, 2π) and strictly decreasing on the interval (0, π).

So, the function is neither increasing or decreasing in (0, 2π). 

Hence proved.

问题 34. 证明 f(x) = x ² – x sin x 是 (0, π/2) 上的递增函数。

解决方案：

We have,

f(x) = x² – x sin x 

On differentiating both sides with respect to x, we get

f'(x) = $\frac{d}{dx}(x^2 - x sin x)$

f'(x) = 2x – (x cos x + sin x) 

f'(x) = 2x – x cos x – sin x

Now for x ∈ (0, π/2), we have

=> 0 ≤ sin x ≤ 1

=> 0 ≤ cos x ≤ 1

So, this implies,

=> 2x – x cos x – sin x > 0

=> f'(x) > 0

Thus, f(x) is an increasing function on the interval (0, π/2).

Hence proved.

问题 35. 求 f(x) = x ³ – ax 是 R 上的递增函数的 a 的值。

解决方案：

We have,

f(x) = x³ – ax

On differentiating both sides with respect to x, we get

f'(x) = $\frac{d}{dx}(x^3 - ax)$

f'(x) = 3x² – a

Now we are given that f(x) = x³ – ax is an increasing function on R, we get

=> f'(x) > 0

=> 3x² – a > 0

=> a < 3x²

The critical point for 3x² = 0 will be 0.

So, we get a ≤ 0.

Therefore, the values of a must be less than or equal to 0.

问题 36. 求 b 的值，其中函数f(x) = sin x – bx + c 是 R 上的递减函数。

解决方案：

We have,

f(x) = sin x – bx + c

On differentiating both sides with respect to x, we get

f'(x) = $\frac{d}{dx}(sin x - bx + c)$

f'(x) = cos x – b + 0

f'(x) = cos x – b 

Now we are given that f(x) = sin x – bx + c is a decreasing function on R, we get

=> f'(x) < 0

=> cos x – b < 0

=> b > cos x

The critical point for cos x = 0 will be 1.

So, we get b ≥ 1.

Therefore, the values of b must be greater than or equal to 1.

问题 37. 证明 f(x) = x + cos x – a 是 R 上所有 a 值的递增函数。

解决方案：

We have,

f(x) = x + cos x – a

On differentiating both sides with respect to x, we get

f'(x) = $\frac{d}{dx}(x + cos x - a)$

f'(x) = 1 – sin x

f'(x) = $sin^2\frac{x}{2}+cos^2\frac{x}{2}-2sin\frac{x}{2}cos\frac{x}{2}$

f'(x) = $(sin\frac{x}{2}-cos\frac{x}{2})^2$

Now for x ∈ R, we have

=> $(sin\frac{x}{2}-cos\frac{x}{2})^2$ > 0

=> f'(x) > 0

Thus, the f(x) is an increasing function on R for all values of a.

Hence proved.

问题 38. 令定义在 [0, 1] 上的 f 是两次可微的，使得 |f”(x)| ≤ 1 对于所有 x ∈ [0, 1]。如果 f(0) = f(1)，则证明对于所有 x ∈ [0, 1]，f'(x) < 1。

解决方案：

As f(0) = f(1) and f is differentiable, we can apply Rolle’s theorem here. So, we get

f(c) = 0 for some c ∈ [0, 1].

On applying Lagrange’s mean value theorem, we get,

For point c and x ∈ [0, 1], so we have

=> $\frac{|f'(x)-f'(c)|}{x-c}=f''(d)$

=> $\frac{|f'(x)-0|}{x-c}=f''(d)$

=> $\frac{|f'(x)|}{x-c}=f''(d)$

As we are given that |f”(d)| ≤ 1 for x ∈ [0, 1], we get

=> $\frac{|f'(x)|}{x-c}$ ≤ 1

=> |f'(x)| ≤ x – c

Now as both x and c lie in [0, 1], therefore x  – c ∈ (0, 1).

This gives us, |f'(x)| < 1 for all x ∈ (0, 1).

Hence proved.

问题 39. 找出 f(x) 增加或减少的区间：

(i) f(x) = x |x|, x ∈ R

解决方案：

We have,

f(x) = x |x|, x ∈ R

=> $f(x)=\begin{cases}-x^2,x<0\\x^2,x>0\end{cases}$

=> $f'(x)=\begin{cases}-2x,x<0\\2x,x>0\end{cases}$

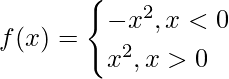
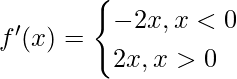
=> f'(x) > 0 for all values of x

Therefore, f(x) is an increasing function for all real values.

(ii) f(x) = sin x + |sin x|, 0 < x ≤ 2π

解决方案：

We have,

f(x) = sin x + |sin x|, 0 < x ≤ 2π

=> $f(x)=\begin{cases}2sinx,0 < x < π\\0,\pi < x \le 2π\end{cases}$

=> $f'(x)=\begin{cases}2cosx,0 < x < π\\0,\pi < x \le 2π\end{cases}$

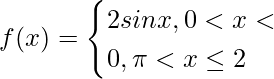
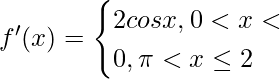
The function cos x is positive between the interval (0, π/2).

Therefore, the function is increasing in the interval (0, π/2).

Also, the function cos x is negative between the interval (π/2, π).

Therefore, the function is decreasing in the interval (0, π/2).

Now for π ≤ x ≤ 2π, value of f'(x) is 0.

Hence the function is neither increasing nor decreasing in the interval (π, 2π).

(iii) f(x) = sin x (1 + cos x), 0 < x ≤ π/2

解决方案：

We have,

f(x) = sin x (1 + cos x)

On differentiating both sides with respect to x, we get

f'(x) = $\frac{d}{dx}(sin x (1 + cos x))$

f'(x) = $sinx(-sinx)+(1+cosx)(cosx)$

f'(x) = –sin² x + cos x + cos²x 

f'(x) = cos² x – sin² x + cos x

f'(x) = cos² x – (1 – cos² x) + cos x

f'(x) = cos² x – 1 + cos² x + cos x

f'(x) = 2 cos² x + cos x – 1

f'(x) = 2 cos² x + 2 cos x – cos x – 1

f'(x) = 2 cos x (cos x + 1) – 1 (cos x + 1)

f'(x) = (2 cos x – 1) (cos x + 1)

For f(x) to be increasing, we must have,

=> f'(x) > 0

=> (2 cos x – 1) (cos x + 1) > 0

=> 0 < x < π/3

=> x ∈ (0, π/3)

For f(x) to be decreasing, we must have,

=> f'(x) < 0

=> (2 cos x – 1) (cos x + 1) > 0

=> π/3 < x < π/2

=> x ∈ (π/3, π/2)

Thus, f(x) is increasing on the interval x ∈ (0, π/3) and decreasing on the interval x ∈ (π/3, π/2).