问题1.以下哪个陈述对一个矩形是正确的?
(i)它有两对相等的边。
(ii)它的所有边都等长。
(iii)对角线相等。
(iv)它的对角线一分为二。
(v)它的对角线是垂直的。
(vi)它的对角线是垂直的,并且一分为二。
(vii)它的对角线相等,并且一分为二。
(viii)它的对角线是相等的,垂直的,并且一分为二。
(ix)所有矩形均为正方形。
(x)所有菱形均为平行四边形。
(xi)所有正方形均为菱形,也为矩形。
(xii)所有正方形都不是平行四边形。
解决方案:
(i) It has two pairs of equal sides.
This statement is True.
(ii) It has all its sides of equal length.
This statement is False because only the pair of opposite sides are equal in a rectangle.
(iii) Its diagonals are equal.
This statement is True.
(iv) Its diagonals bisect each other.
This statement is True.
(v) Its diagonals are perpendicular.
This statement is False because diagonals are not perpendicular.
(vi) Its diagonals are perpendicular and bisect each other.
This statement is False because diagonals are not perpendicular, they only bisect each other.
(vii) Its diagonals are equal and bisect each other.
This statement is True.
(viii) Its diagonals are equal and perpendicular, and bisect each other.
This statement is False because the length of the diagonals are equal, and they bisect each other, but they are not perpendicular.
(ix) All rectangles are squares.
This statement is False because all the rectangles are not square.
(x) All rhombuses are parallelograms.
This statement is True.
(xi) All squares are rhombuses and also rectangles.
This statement is True.
(xii) All squares are not parallelograms.
This statement is False because the opposite sides are parallel and equal, so all squares are parallelograms.
问题2.以下哪个陈述适用于正方形?
(i)这是一个矩形。
(ii)它的所有边都等长。
(iii)它的对角线彼此成直角一分为二。
(v)它的对角线等于它的边。
解决方案:
(i) It is a rectangle.
This statement is True.
(ii) It has all its sides of equal length.
This statement is True.
(iii) Its diagonals bisect each other at right angle.
This statement is True.
(v) Its diagonals are equal to its sides.
This statement is False because the length of the diagonals are not equal to the length of the sides of the square.
问题3.在以下每个栏中填写空白,以使陈述正确:
(i)矩形是其中________的平行四边形。
(ii)正方形是__________的菱形。
(iii)正方形是其中___________的矩形。
解决方案:
(i) A rectangle is a parallelogram in which one angle is a right angle.
(ii) A square is a rhombus in which one angle is a right angle.
(iii) A square is a rectangle in which adjacent sides are equal.
问题4.窗框的对角线长于另一对角线。窗框是矩形吗?为什么或者为什么不?
解决方案:
The window frame is not a rectangle because the length of the diagonals of a rectangle are equal.
问题5.在矩形ABCD中,证明ΔACB≅ΔCAD。
解决方案:
Draw a rectangle,
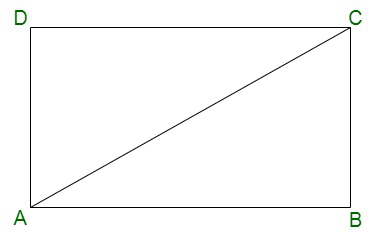
Now in the given figure
Diagonal = AC
So, in ΔACB and ΔCAD
AB = CD [Opposite sides of a rectangle are equal]
BC = DA
AC = CA [Common Sides]
So, by SSS both the triangles are congruent
ΔACB ≅ ΔCAD
问题6.矩形的边之比为2:3,其周长为20厘米。绘制矩形。
解决方案:
Given: Perimeter = 20cm
Ratio = 2:3
Let ABCD is a rectangle
So, let us assume ‘x’ be the side of rectangle
Length(l) = 3x
Breadth(b) = 2x
By using the formula, we get
Perimeter of the rectangle = 2(length + breadth)
20 = 2(3x + 2x)
10x = 20
x = 20/10 = 2
Hence, Length = 3×2 = 6cm and breadth = 2×2 = 4cm
So, now we draw a rectangle of length = 6cm and breadth = 4cm.
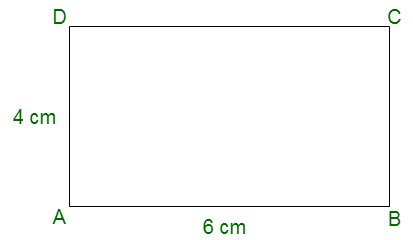
问题7.矩形的边之比为4:5。如果周长为90厘米,则找到矩形的边。
解决方案:
Given: Perimeter = 90cm
Ratio = 4:5
Let ABCD is a rectangle
So, let us assume ‘x’ be the side of rectangle
Length (l) = 5x
Breadth (b) = 4x
By using the formula, we get
Perimeter of the rectangle = 2(length + breadth)
90 = 2(5x + 4x)
18x = 90
x = 90/18 = 5
Hence, Length = 5×5 = 25cm and Breadth = 4×5 = 20cm
So, now we draw a rectangle of length = 25cm and breadth = 20cm.

问题8.求出边长分别为12厘米和5厘米的矩形的对角线长度。
解决方案:

Given that in rectangle ABCD,
AB = 12cm
BC = 5cm
Find: the length of AC
In ΔABC
By using Pythagoras theorem,
AC2 = AB2 + BC2
AC2 = 122 + 52
AC2 = 144 + 25
AC2 = 169
AC = √169
AC = 13cm
Hence, the length of the diagonal AC = 13cm.
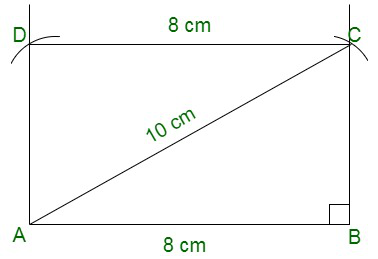
问题9.绘制一个矩形,该矩形的一侧长8厘米,每个对角线的长度为10厘米。
解决方案:
Given that
One side of the rectangle = 8cm.
Diagonal length = 10cm
So, Now we are going to construct a rectangle using the following steps:
(i) Draw a line named as AB of length 8 cm.
(ii) Now, from point A create an arc of length 10 cm and mark it as a point C.
(iii) Now draw a 90° angle from point B and then join the arc from point A which cuts at point C.
(iv) Join lines AC and BC.
(v) Now draw a 90° angle from point A and cut an arc from C point of length 8 cm for D point
(vi) Now, join lines CD and AD
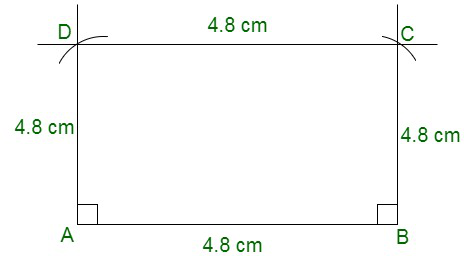
问题10.画一个正方形,每边长4.8厘米。
解决方案:
Given that
Side = 4.8cm.
So, Now we are going to construct a square using the following steps:
(i) Draw a line named as AB of length 4.8 cm.
(ii) Now draw perpendiculars(90° angle) from points A and B.
(iii) From point A and B create an arc of length 4.8 cm on the perpendiculars to get point D and C.
(iv) After creating arc join line DC, AD and BC.
问题11.确定具有以下各项的所有四边形:
(i)四边相等的长度
(ii)四个直角
解决方案:
(i) Square and Rhombus.
(ii) Square and Rectangle.
问题12.解释正方形
(i)四边形?
(ii)平行四边形?
(iii)菱形?
(iv)矩形?
解决方案:
(i) A square is a quadrilateral because it has all sides of equal length.
(ii) A square is a parallelogram because the opposite sides of a square are equal and parallel.
(iii) A square is a rhombus because all sides of a square are of equal length and the opposite sides are parallel.
(iv) A square is a rectangle because the opposite sides of a square are equal and each angle is of 90°.
问题13:命名对角线的四边形:
(i)彼此一分为二
(ii)彼此垂直平分
(iii)相等。
解决方案:
(i) Parallelogram, Rectangle, Rhombus and Square.
(ii) Rhombus and Square.
(iii) Square and Rectangle.
问题14. ABC是直角三角形,O是与直角相反的一侧的中点。解释为什么O与A,B和C等距。
解决方案:

Given that triangle ABC is a right-angled triangle, in which O is the midpoint of hypotenuse AC
So, OA = OC
Now, we draw CD||AB and join AD,
such that AB = CD and AD = BC.
So, the quadrilateral ABCD is a rectangle because each angle is a right
angle and opposite sides are equal and parallel.
So, AC = BD [Length of the diagonals are equal]
AO = OC = BO = OD
Therefore, O is equidistant from A, B and C.
问题15.泥瓦匠做了一块混凝土板。他需要它是矩形的。他可以通过哪些不同方式确保它是矩形的?
解决方案:
The concrete slab can be a rectangle if each angles is 90° and the diagonals are equal.