简谐运动的力定律

你有没有想过，为什么当我们拉伸松紧带然后松开它时，它会恢复到原来的状态？它被一种力量强迫恢复到原来的状态。但这股力量究竟是什么？让我们研究这个力并发展简谐运动的力定律。

周期性运动是我们已经熟悉的东西。周期性运动被定义为以相等的时间间隔重复自身的运动。例如，时钟指针的运动、汽车车轮的运动和旋转木马的运动。在自然界中，所有这些运动都是重复的。他们在一段时间后重复自己。

振荡运动是一种周期性运动，其中项目围绕其平衡位置振荡。在给定的时间后，该项目重复相同的移动序列。振荡就是这样的一系列运动。在基本摆的运动、树叶在微风中的运动和摇篮的运动中可以看到振荡运动。

简谐运动 (SHM)

Simple harmonic motion is the most basic type of oscillatory motion. When an object moves in a straight path, it exhibits simple harmonic motion. All oscillatory motion examples are instances of basic harmonic motion. 

摆动基本摆会使其远离平均平衡点。当它到达其具有最大位移的极端位置时，它会停下来，它的速度变为零。由于作用在平衡位置方向的力，它返回到其平衡位置。

它现在穿过其正常位置，但不会停止。它转移到另一个极端位置。之后，它又回到了原来的位置。振荡是一种全运动。基本摆的摆动是简谐运动的一个很好的例证。

因此，如果作用在物体上的恢复力与从平均位置的位移成正比并且总是倾向于反对它，则称物体的运动为简谐运动。恢复力的方向与位移的方向相反。

以简谐运动运动的粒子的加速度由下式给出，

a(t) = -ω ² x(t)

其中 ω 是粒子的角速度。

现在让我们讨论一些与粒子的简谐运动相关的重要术语：

1. 位移 (x)：任何时刻的位移定义为执行 SHM 的身体从其平均或平衡位置行进的净距离。
2. 幅度 (A)：振荡幅度定义为身体在平均位置两侧执行 SHM 的最大位移。
3. 速度 (v)：任何时刻的速度定义为位移随时间的变化率。对于执行 SHM 的物体，其速度在平均位置最大，在极端位置最小（零）。物体的速度与从平均位置的位移成反比。
4. 加速度 (a)：加速度定义为速度随时间的变化率。与速度不同，加速度与位移成正比。它在位移最大的极端位置最大，在平均位置（位移 = 0）最小。
5. 恢复力 (F _R )：恢复力是始终作用于与位移方向相反但与其成正比的力。恢复力在极端位置最大，在平均位置最小。
6. 弹簧常数 (k)：弹簧常数是特定弹簧的常数值，它确定将弹簧压缩或拉伸 1 个单位所需的力的大小。
7. 能量（E）： SHM下物体的总能量称为机械能，如果介质是无摩擦的，物体的机械能在整个运动过程中保持不变。物体在任何时刻的机械能是其动能和势能的总和。
8. 时间周期 (T)：振荡的时间周期定义为身体完成一次振荡所用的时间。换句话说，就是覆盖4倍幅度所用的时间。
9. 频率 (f)：频率定义为身体在一秒钟内产生的振动次数。它是时间段的倒数。 f = (1/T)

Note: In periodic motion, the direction of restoring force may or may not be in the direction of displacement but in Simple Harmonic Motion (SHM) the direction of restoring force is always opposite to the direction of displacement. This leads to the fact that all Simple Harmonic Motions are periodic motions but vice versa is not true.

简谐运动的力定律

让我们用一个例子来发展简谐运动的力定律。简谐运动最基本的例子是弹簧块系统。考虑一个连接到弹簧的质量 m 块，然后将其连接到坚硬的墙上。该块由无摩擦表面支撑。

当我们不拉它时，弹簧处于平衡位置，也就是没有力施加在它上面的时候。在这种情况下，作用在其上的合力为零。让我们尝试两种不同的方法，看看会发生什么。

1. 当我们将块向外移动时，一个力作用在它上面，试图将它向内拉，朝向它的平衡位置。
2. 当我们向内压块时，作用在它上面的力会试图将它向外推向平衡位置。

在这两种情况下，我们都可以观察到有一个力作用在块上，试图让它回到平衡位置。这个力就是恢复力，它是简谐运动力定律的基础。让我们弄清楚如何应用这个概念。

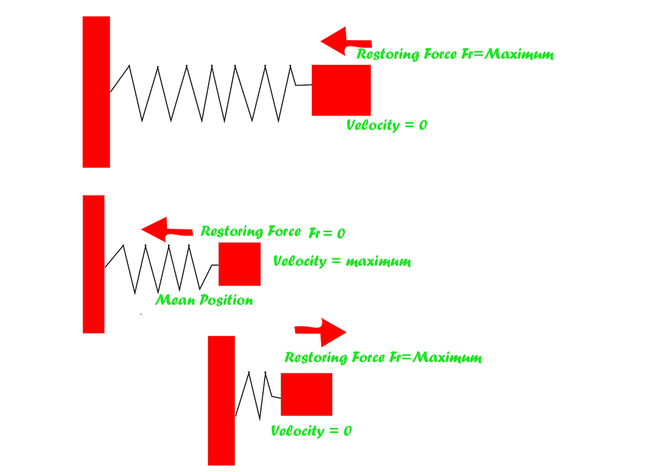
恢复力随位移的变化而变化

Let F be the restoring force and x denote the displacement of the block from its equilibrium position. As a result of our observations, we may conclude that the restoring force is directly proportional to the displacement from the mean position.

This implies, 

F = – kx                                                                                                                                                                                                    ……(1)

where k is known as the force constant. It is measured in N/m in the SI system and in dynes/cm in the C.G.S. system. The negative symbol denotes that the restoring force and displacement are always pointing in opposing directions. For simple harmonic motion, equation (1) is the simplest version of the force law.

It demonstrates the fundamental law of simple harmonic motion, which states that force and displacement must be in opposing directions.

We also know that: 

F = ma

As a result, 

a = F/m

Substituting the value of F from equation (1) which yields,

a = – kx/m = – ω²x                                                                                    (where k/m = ω²)                                                               ……(2)

As a result, Equations I and II are the force laws of simple harmonic motion. It should be noted that the restoring force is always directed towards the mean position and in the opposite direction of displacement.

例子：

If the force required to stretch a spring  by 50 cm is 150 N. How much force is

required to compress it by 35 cm?

Solution:

According to Hooke’s law: F_R = -kx

  In the first case: x= -50 cm = -0.5 m

[x is taken negative to indicate that it is opposite to F_R]

               

         F_R = 150 N

          k = (- 150/-0.5) N/m          

          k = 300 N/m

  In the second case:

         x= 35 cm = 0.35 m

       F_R= -300 * 0.35 N

        =  -105 N

微分方程

We know Force = mass * acceleration.

Acceleration (a) of a body in SHM is given by:

a = d²x/dt² [Acceleration is the rate of change of velocity, a = (dv/dt) and v = (dx/dt)]

Force (F) = mass (m) * acceleration (a).

Now according to Hooke’s law,

F_R = -kx, F = F_R  [F is the force applied and F_R is the restoring force]

Therefore: -kx = m * a

                 -kx = m * d²x / dt²

                  d²x / dt²= (-k * x) / m

Note: Restoring Force is zero at the mean position because at mean position the value of x ix zero.

在 SHM 中完成的工作

Work done = Force * Displacement, you might be thinking that as the applied force is equal to the

restoring force which is kx (magnitude) and the displacement is x so the work done should be kx²,  

but this is not the case here, we cannot use W = Force * Displacement because this definition or formula

of work done is applicable only when the force is constant but in SHM, force is a function of displacement

from the mean position.

The formula for work done in the case of SHM :

W = (1/2) ∗ k ∗ x²

Proof:

For variable force,

W = ∫ F dx

W = ∫ kx dx [F = kx]

W = (1/2) ∗ k ∗ x²

This is also the formula for the potential energy of the mass-spring system denoted by U_X

SHM 与匀速圆周运动的关系。

如果物体与固定点（中心）的距离在整个运动过程中保持恒定，则称该物体的运动是圆形的。

如果运动中的物体的速度保持不变，则称圆周运动是均匀的。

注意：速度保持不变，但速度不变，因为运动方向不断变化。匀速圆周运动是

加速运动。

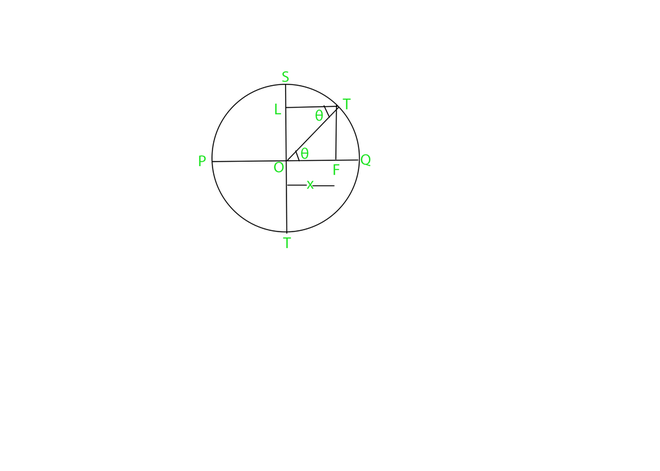
物体的匀速圆周运动

考虑到上图，匀速圆周运动下物体在直径上的投影称为简谐运动。

如果我们考虑身体的侧向运动，它看起来好像身体正在沿着直径与中心的直线路径移动

圆为平衡位置。

SHM 中的位移

In the figure, ‘θ’ is the angular displacement, ‘x’ is the linear displacement of the body under SHM.

                                                                       cos θ = Base / Hypotenuse,

                                                                       cos θ = OF / OT

                                                                       cos θ  = x / A, x is the displacement from the mean position and A is the amplitude

                                                                       x = A cos θ — Equation of displacement of a body under SHM.

                                                                       x = A cos(ωt), ω is the angular velocity or frequency,  θ = ωt.

                                                                       x = A cos (2πft), ω = 2πft

The maximum value of the cosine of any angle is +1 (positive direction) and -1 (negative direction), considering this the maximum value of x can be A (magnitude),

which is the amplitude of oscillation or vibration.

The equation can also be written in the form of sine of the angular displacement, y = A sin θ.

SHM 中的速度

As discussed, velocity is defined as the rate of change of displacement with time.

                                                                                                                          v = d(x) / dt

                                                                                                                          v = d(A cos (ωt)) / dt

                                                                                                                          v =(-A sin (ωt)) * ω

                                                                                                                          v = -V sin (ωt) — Equation of velocity, V= Aω.

‘V’ is the velocity with which the body is revolving in the circular path. Linear Velocity = Angular Velocity * Radius of the circle.

‘ω’ is the angular velocity, ‘A’ is the amplitude which in turn is the radius of the circle, hence we can write ‘V’ in place

of ‘Aω’.

In △ TOF, sin (ωt) =  (TF) / (TO),

               sin (ωt) = √(A² – x²) / A [By Pythagoras Theorem, Hypotenuse² = (Perpendicular)² + (Base)², TF = √(A²– x²)]                                                                                          

Replacing the value of sin (ωt) in the equation of velocity,

          v =( -V * √(A² – x² )) / A — Another form of equation of velocity.

In the above equation, if the value of x is equal to A i.e. if the displacement is maximum then the value of v is zero and

if the value of x is zero i.e. if the body is at the mean position then the value of v is max.

‘V’ is the velocity of the body executing uniform circular motion and also the maximum velocity

of the body executing simple harmonic motion.

SHM 中的加速

Acceleration (a)  is defined as the rate of change of velocity with time.

                                                                                                 v = -A sin (ωt)) * ω — Equation of velocity

                                                                                                 a = d(v) / dt

                                                                                                 a = d((-A sin (ωt)) * ω) / dt

                                                                                                 a= -A cos (ωt) * ω²  — Equation of acceleration

In △ TOF, cos (ωt) = (OF) / (OT)

               cos (ωt) = x / A

Replacing the value of cos (ωt) in the equation of acceleration,

                                                                                                  a = (-A * x * ω² ) / A

                                                                                                  a = – xω² — Another form of the equation of acceleration

Considering the above equation, if the value of x is zero then acceleration is also zero which proves the fact that acceleration is zero at the mean position.

On the other hand, if the value of x is maximum i.e. ‘A’ then the value of acceleration is also maximum.

                                                         a_max = -Aω² — Equation for maximum acceleration

SHM 中的时间段

Time Period of Oscillation is given by,

                                                           T = (2πR) / V, 2πR is the circumference of the circle and  V is the linear velocity,

                                                           T = (2π) /  ω,     V = ω * R.

                                                            T = (2π) / √(a / x),     ω = √(a / x)

                                                            T =  (2π) * √(x / a)

Hence the time period of oscillation is given by Time Period = (2π) * √(displacement / acceleration).

SHM 中的频率

Frequency is the total number of vibrations or oscillations made by the body in one second.

                                                                                                                                               f = (1/ Time Period)

                                                                                                                                                f = (1/2π) * √(acceleration / displacement)

动能

This energy of the body is due to the motion of the body.

                                                                                    K = (1/2) * m * v²

                                                                                    K = (1/2) * m * (ω * √(A² – x² ))²,    v = ω * √(A² – x²)

                                                                                    K = (1/2) * m * ω ² * (A² – x² )

At x = 0, the value of  K is maximum.

                                                         K_max = (1/2) * m * ω ²* (A²)

At x= A, the value of K is zero.

势能

This energy of the body is due to the position of the body or the amount of work done by the body.

                                                                                                                                                               U = (1/2) * m * ω² * x²

Potential Energy is maximum at the extreme positions where the value of displacement is equal to Amplitude and minimum at the equilibrium position

where the displacement is zero.

                                                 U_max = (1/2) * m * ω ² * A²

单摆

另一个执行 SHM 的物体的例子是一个简单的钟摆，一个简单的钟摆

由从线程中暂停的 bob 组成。如果我们忽略线的质量和周围的摩擦

该系统则将该运动称为 SHM。

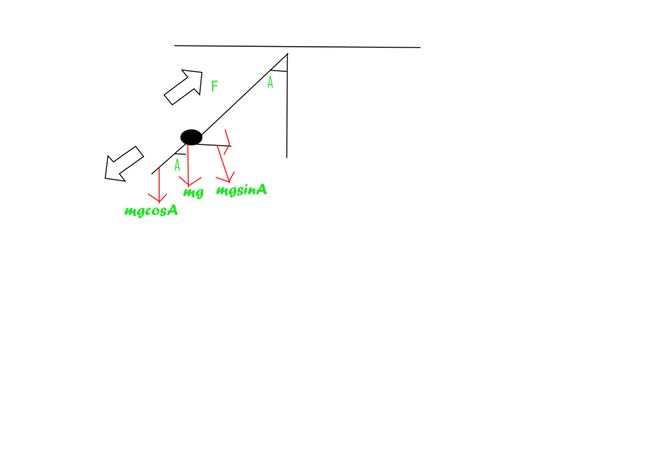
作用在执行 SHM 的 bob 上的力

考虑到上图：

The effect of mgcosA is cancelled by Force of Tension [F] as both are acting opposite
to each other. This is why the bob is having zero movement in the vertical direction.
The restoring force is being generated due to mgsinA which is in the direction opposite
to that of displacement.

FR = -mgsin(∠A), now if the angular displacement i.e. ∠A is very small then
∠A = sin(∠A) [Unit of angle is radian]
Therefore, FR = -mg∠A, now ∠A =x/l where x is the linear displacement of the bob
from the mean position and l is the length of the rope or thread used.
Substituting the value of ∠A, we get:
           FR = -mg(x/l)          
The expression states that the restoring force is directly proportional and opposite in direction
to the displacement from the mean position.

示例问题

问题 1：将弹簧拉伸 10 厘米所需的力为 150 N。将弹簧拉伸 100 厘米需要多大的力？计算弹簧的弹簧常数。

解决方案：

As long as the external force is applied on the body, the restoring and the applied force are the same, then

F = -kx

Since, it is given that, F = 150 N

x = -10 cm = – 0.1 m (Taking x negative because we have taken force as positive)

Therefore, k = (150 / 0.1) = 1500 N/m

Now, x = -100 cm = -1 m

F = -kx

F = -(1500) × -1

F = 1500 N

Thus, Spring Constant = 1500 N/m

问题 2：计算将弹簧常数为 1000 N/m 的弹簧压缩 30 m 所做的功。

解决方案：

Work done = (1/2) × k × x²

                   = (1/2) × 1000 × (30)² Nm or Joule

                   = 500 × 900 Joule

                   = 450000 Joule         

问题 3：一个物体做圆周运动，时间周期等于 10 秒。考虑物体沿圆形路径直径的运动。如果在距平均位置的位移处作用在身体上的力为 200 N，则求该点的加速度。 （考虑弹簧常数 = 100 N/m 的弹簧直径）

解决方案：

Given that, T = 10 seconds

According to Hooke’s law, F = -kx

200 = -(100) * x

x = -2 m [Negative sign indicates that the direction of displacement is opposite to that of force]

Acceleration = -ω²x

ω = 2πf, 

where f is the frequency of oscillation given by, 

f =1/T

f = (1/10) Hz, 

And

ω = 2 × 3.14 × 0.1

    = 0.628 radian/second

Acceleration = -(0.628)² × (-2) m/s²

                          = 0.788768 m/s²

问题 4：质量为 10 Kg 的物体从最大位移位置开始 2 秒后的速度为 3 m/s。如果频率为（1/8）Hz，求该点的势能和动能，甚至求总能量。

解决方案：

Since, K = (1/2) × m × v²

                    = (1/2) × 10 × 9 J

                    = 45 J

  ω = 2πf

      = (2 × 3.14) / 8

      = 0.785 radians/second

Instantaneous velocity is given by,

v = A × ω × sin (ωt)                                                                                                  (Neglecting the negative sign)

3 = A × (0.785) × sin((π/4) × 2)),  

0.785 = (π/4) (approx)

or

A = 3 / 0.785 m

A = 3.8217 m

Total Energy(E) = (1/2) * m * ω² * A² 

                         = (1/2) * 10 * (0.785)² * (3.8217)²

                         = 45 J

Potential Energy(U) = Total Energy(E) – Kinetic Energy(K)

                                = 45 – 45 J

                                 = 0 J

This indicates that the body is at the mean position.

问题5：弹簧常数的意义是什么？写出弹簧常数的尺寸。

解决方案：

Spring constant of a spring is the amount of force required to stretch or compress the given spring by unit displacement. It is used to compare the stiffness of two springs. The one with greater spring constant has more stiffness i.e. is more difficult to deform compared to the one having lower spring constant. 

In other words, the amount of work done to stretch or compress a spring (mass-spring system) is directly proportional to its spring constant. Higher the spring constant, higher the amount of work done to stretch or compress it. Unit of Spring Constant is N/m. And the Dimension of Spring Constant is [M L⁰ T^-2].

问题 6：推导 SHM 下身体势能的表达式。

Solution:

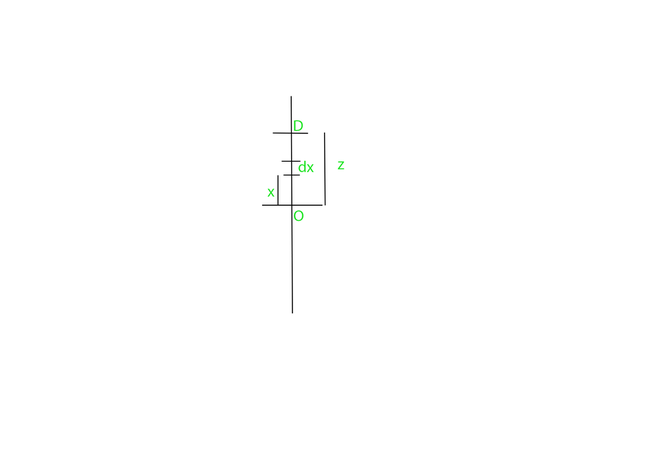
Derivation of Potential Energy

Force = mass * acceleration
    F = m * a
     F = m * -ω2 * x
We know that Work done = Force * Displacement, but we cannot use this formula directly in SHM  because force is not constant.
    dW = F . dx, where dW is the work done for a very small-displacement dx.
   dW = (-m * ω2 * x) * dx * cos(180°)  [ Cross product of F and dx, as both are opposite to each other hence the angle between them is 180°]
   dW = m * ω2 * x * dx
To calculate the work done in moving the particle from O to D, we integrate the above equation between the limits 0 to z:
                   ∫ dW = ∫ m * ω2 * x  dx
                    W   = (1/2) * m * ω2 * z2 [On putting the limits]
This in turn is the potential energy of the body.

问题 7：简单谐波运动中物体运动的频率是 10 Hz。计算位移 3 m 时作用在物体上的力

从平均位置。身体的质量是 12 公斤。

Solution:

             Given,

                         f = 10 Hz

                         ω = 2 * π * f

                             = 2 * 3.14 * 10 radian/second

                             = 62.8 radian/second

                       acceleration(a) = -ω ²* x

                                       = -(62.8)2 * 3

                                       = -11831.52 m/s²

                     Force = mass * acceleration

                           = 12 * 11831.52 N

                     Force = 141978.24 N

问题 8：物体在 SHM 中移动，距离平均位置 3 m，受力为 200 N。物体的质量为 50 kg，

找到振荡频率。

Solution:

              Given,

                         F = 200 N

                         F = m * a

                        200 = 50 * a

                         a = 4 m/s²

                We know,

                           a = -ω² * x

                           4 = -ω² * (-3) [Taken x as negative to state that its direction is opposite to that of acceleration or vice versa]

                           ω = 2 / √(3)

                           ω = 1.1547 radian/second (approx)

                           ω = 2 * π * f

                           f = (1.1547) / (2 * 3.14)

                           f = 0.1839 Hz (approx)

问题 9：一个物体正在进行 SHM，时间周期等于 20 秒。身体的质量是 30 公斤。找到作用在身体上的力

距平均位置 4 m。

Solution:

                   Given,

                           T = 20 seconds

                           T = 2 * π * √(x / a)

                           20 = 2 * 3.14 * √(4 / a)

                           a = 0.394 m/s

                           F = m * a

                           F = 30 * 0.394 N [Mass = 30 kg]

                           F = 11.82 N

问题 10：在 SHM 中，势能和动能值在什么位置最大？

Solution:

            Potential Energy is maximum at the extreme positions i.e. when the value of x is equal to A (amplitude) i.e

            when the value of displacement is maximum.

            Kinetic Energy is maximum at the equilibrium position because kinetic energy depends on the velocity and

            since the velocity is maximum at the equilibrium position (x = 0), hence Kinetic Energy is also maximum.  

问题 11：主体执行 SHM，周期为 20 秒。在它通过它的振荡中心三秒后，它的速度

发现为 2 m/s。找到幅度。

Solution:    

         We know,

                 v = -A * ω * sin(ωt), v is the velocity, ω is the angular velocity and t is the time.

                 Given,

                        T = 20 seconds

                        ω = 2 * π * f

                          = 2 * π  * (1 / 20) — f = 1 / T.

                Note: We cannot take t = 3 because we have derived all the equations of simple harmonic motion

                      considering the motion  to be starting from extreme position hence we need

                      to subtract the time from the (time period / 4) to get the actual time.

                      t =  (20 / 4) – 3

                        =   2

                     Now,

                         v = -A * ω * sin(ωt)

                         2 = -A * (2 * π * (1 / 20)) * sin(2 * π * (1 / 20) * 2)

                         A = -10.84  m

                         [Neglecting the minus sign]

                         Amplitude = 10.84 m.

问题12：物体的匀速圆周运动是简谐运动的例子吗？

Solution:

                 No, the uniform circular motion of a body is not simple harmonic motion, it is not even an oscillatory motion.

                 It is a periodic motion.

                 All simple harmonic motions are periodic motions but all periodic motions are not simple harmonic motions.

                If we consider the motion of the body along the diameter of the circle then it is a simple harmonic motion.

问题 13：作用在执行简谐运动的物体上的力是否取决于平均位置的位移？

Solution:

          Yes, force is directly proportional to the displacement from the mean position.

          It is zero at the equilibrium position (x = 0) and maximum at the extreme positions where the value of displacement is maximum.

                  According to Hooke’s law,

                                          F = -kx, where k is the spring constant and x is the displacement from the equilibrium position.

问题 14：物体的振动频率为 f。它的动能振荡的频率是多少？

   Solution :

                   As the Kinetic Energy becomes zero and maximum twice in course of one full oscillation hence it oscillates at frequency 2 * f.

问题15：SHM中振荡的粒子的位移和加速度的相位差是多少？

Solution:

                 Zero, there is no phase difference between displacement and acceleration.