第十类RD Sharma解决方案–第七章统计–练习7.6

问题1.用以下方法得出一个小于以下数据的对象：

No. of rooms	1	2	3	4	5	6	7	8	9	10
No. of houses	4	9	22	28	24	12	8	6	5	2

解决方案：

We plot the points (1, 4), (2, 13), (3, 35), (4, 63), (5, 87), (6, 99), (7, 107), (8, 113), (9, 118), (10, 120) respectively by taking the upper-class limit over the x-axis and cumulative frequency over the y-axis of the graph.

问题2：750名学生在考试中获得的分数以频率分布表的形式给出：

No. of rooms	No. of houses	Cumulative Frequency
Less than or equal to 1	4	4
Less than or equal to 2	9	13
Less than or equal to 3	22	35
Less than or equal to 4	28	63
Less than or equal to 5	24	87
Less than or equal to 6	12	99
Less than or equal to 7	8	107
Less than or equal to 8	6	113
Less than or equal to 9	5	118
Less than or equal to 10	2	120

用不到的方法准备一个累积频率分布表，并画一个图。

解决方案：

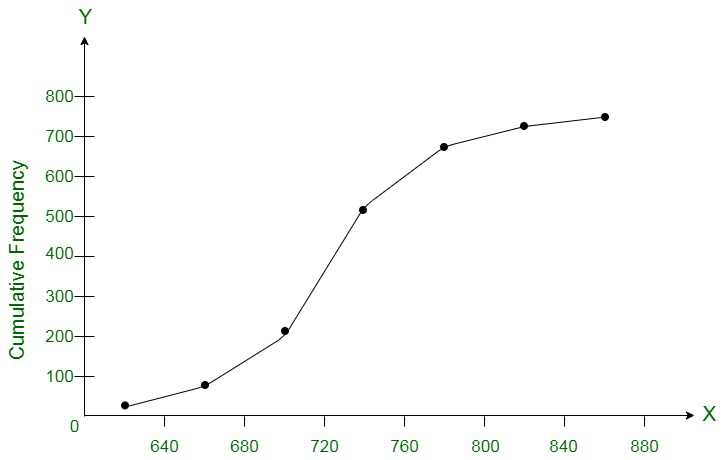
问题3.绘制一个Ogive来表示以下频率分布：

Marks	No. of Students
600 – 640	16
640 – 680	45
680 – 720	156
720 – 760	284
760 – 800	172
800 – 840	59
840 – 880	18

解决方案：

Converting the given frequency distribution into continuous frequency distribution:

We plot the specified points (4.5, 2), (9.5, 8), (14.5, 18), (19.5, 23), (24.5, 26) on a graph by taking the upper class limit over the x-axis and cumulative frequency over the y-axis respectively.

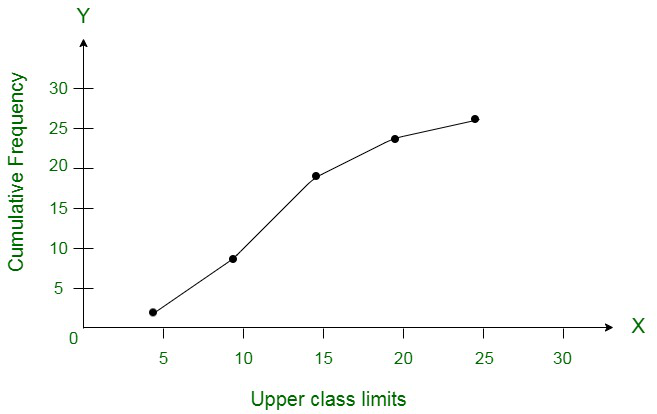
问题4. 100家商店的月利润(以卢比计)分配如下：

Marks	No. of Students	Marks Less than	Cumulative Frequency
600 – 640	16	640	16
640 – 680	45	680	61
680 – 720	156	720	217
720 – 760	284	760	501
760 – 800	172	800	673
800 – 840	59	840	732
840 – 880	18	880	750

为其绘制频率多边形。

解决方案：

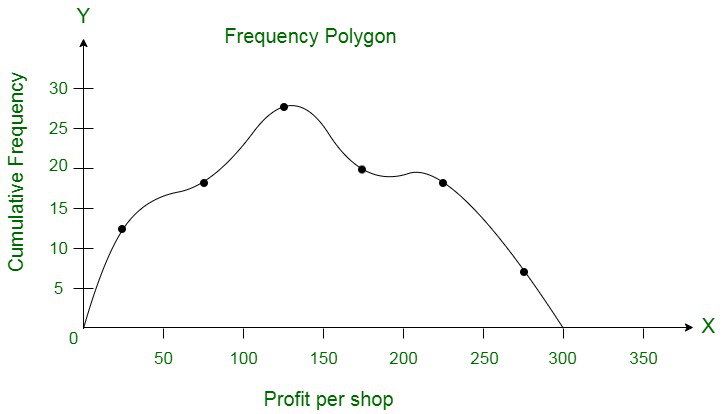
Now, computing the following data, we have,

Now, the frequency polygon can be computed as follows :

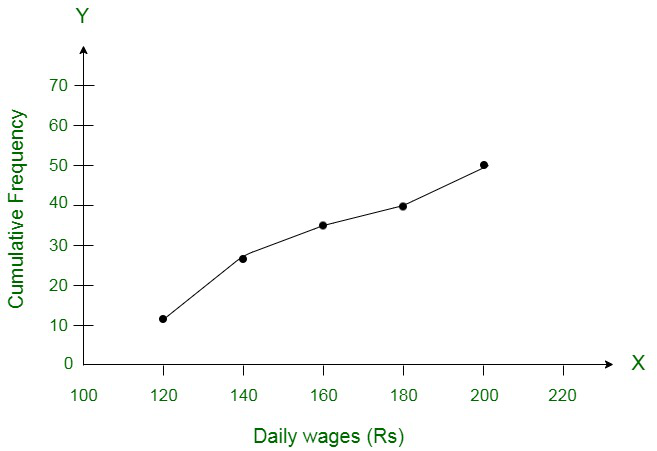
问题5.以下分配给出了一家工厂50名工人的日收入：

Class-interval	0 – 4	5 – 9	10 – 14	15 – 19	20 – 24
No. of students	2	6	10	5	3

将上述分布转换为“小于”类型的累积频率分布，并得出其目标。

解决方案：

Using the less than method, the following distribution can be converted to a continuous distribution, as,

Mark the point (120, 12), (140, 26), (160, 34), (180, 40), (200, 50), taking upper class limit on the x-axis and cumulative frequencies on y-axis respectively. 

问题6.下表列出了一个村庄的100个农场的每公顷小麦的产量：

Class-interval	No. of Students	Less than	Cumulative frequency
0.5 – 4.5	2	4.5	2
4.5 – 9.5	6	9.5	8
9.5 – 14.5	10	14.5	18
14.5 – 19.5	5	19.5	23
19.5 – 24.5	3	24.5	26

画“小于”，“大于”。

解决方案：

(i) Computing the Less than ogive

Production yield  in kg 1 hectare	Class	No. of farms. (f)	c.f.
Less than 55	50-55	2	2
Less than 60	55-60	8	10
Less than 65	60-65	12	22
Less than 70	65-70	24	46
Less than 75	70-75	38	84
Less than 80	75-80	16	100

We plot the specified points (55, 2), (60, 10), (65, 22), (70, 46), (75, 84) and (80, 100) and connect them to form an ogive. 

(ii) More than
 

Production yield	c.f.	Class
More than or equal to 50	100	50-55
More than or equal to 55	84	55-60
More than or equal to 60	46	60-65
More than or equal to 65	22	65-70
More than or equal to 70	10	70-75
More than or equal to 75	2	75-80
More than or equal to 80	0	80-85

We plot the specified points (50, 100), (55, 84), (60, 46), (65, 22), (70, 10), (75, 2) and (80, 0) and connect to form a more than ogive as shown below:
 

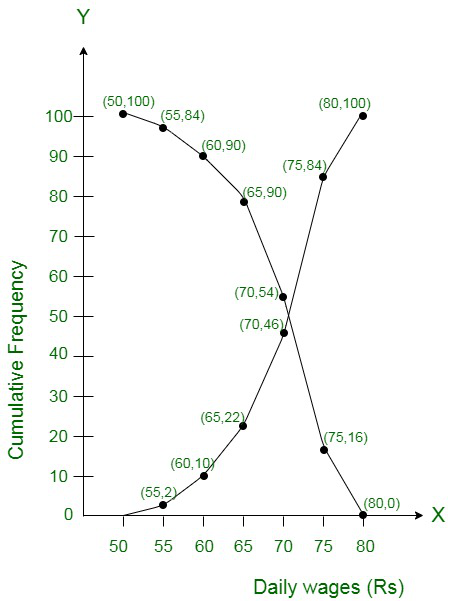
问题7.在对35名班级学生进行身体检查时，他们的体重记录如下：

Profit per shop	No of shops:
0 – 50	12
50 – 100	18
100 – 150	27
150 – 200	20
200 – 250	17
250 – 300	6

为给定数据绘制小于类型的ogive。因此，从图表中获得体重的中位数，并使用公式验证结果。 (CBSE 2009)

解决方案：

Weight (in Kg)	Number of students	Class	c.f.
Less than 38	0	36-38	0
Less than 40	3	38-40	3
Less than 42	5	40-42	2
Less than 44	9	42-44	4
Less than 46	14	44-46	5
Less than 48	28	46-48	14
Less than 50	32	48-50	4
Less than 52	35	50-52	3

Plot the points (38, 0), (40, 3), (42, 5), (44, 9), (46, 14), (48, 28), (50, 32), (52, 35) on the graph and join them in free hand to get an ogive as shown.

Here N = 35 which is odd

∴ $\frac{N}{2}=\frac{25}{2}$ = 252 = 17.5

From 17.5 on y-axis draw a line parallel to x-axis meeting the curve at P. From P, draw PM ⊥ x-axis

∴ Median which is 46.5 (approx)

Now N = 17.5 lies in the class 46 – 48 (as 14 < 17.5 < 28)

∴ 46-48 is the median class

Here l= 46, h = 2,f= 14, F= 14

∴ Median = $l+\frac{\frac{N}{2}-F}{f}\times h=46+\frac{17.5-14}{14}\times2=46+\frac{3.5\times2}{14}=46+0.5=46.5$  

问题8.以下选项卡中给出了一个城市66天的年度降雨量记录

Profit per shop	Mid-value	No of shops:
Less than 0	0	0
Less than 0 – 50	25	12
Less than 50 – 100	75	18
Less than 100 – 150	125	27
Less than 150 – 200	175	20
Less than 200 – 250	225	17
Less than 250 – 300	275	6
Above 300	300	0

使用大于类型和小于类型的输入来计算平均降雨量。 [NCERT示例]

解决方案：

We observe that, the annual rainfall record of a city less than 0 is 0. Similarly, less than 10 include the annual rainfall record of a city from 0 as well as the annual rainfall record of a city from 0-10. So,

the total annual rainfall record of a city for less than 10 cm is 0 + 22 = 22 days. Continuing in this manner, we will get remaining less than 20, 30, 40, 50 and 60.Also, we observe that annual rainfall

record of a city for 66 days is more than or equal to 0 cm. Since, 22 days lies in the interval 0-10. So, annual rainfall record for 66 – 22 = 44 days is more than or equal to 10 cm. Continuing in this

manner we will get remaining more than or equal to 20, 30 , 40, 50, and 60.

Now, we construct a table for less than and more than type.

(i) Less than type		(ii) More than type
Rainfall (in cm)	Number of days	Rainfall (in cm)	Number of days
Less than 0	0	More than or equal to 0	66
Less than 10	0+22=22	More than or equal to 10	66-22=44
Less than 20	22+10=32	More than or equal to 20	44-10=34
Less than 30	32+8=40	More than or equal to 30	34-8=26
Less than 40	40+15=55	More than or equal to 40	26-15=11
Less than 50	55+5=60	More than or equal to 50	11-5=6
Less than 60	60+6=66	More than or equal to 60	6-6=0

To draw less than type ogive we plot the points (0,0), (10,22), (20,32), (30, 40), (40, 55), (50, 60), (60, 66) on the paper and join them by free hand.

To draw the more than type ogive we plot the points (0, 66), (10, 44), (20, 34), (30, 26), (40, 11), (50, 6) and (60, 0) on the graph paper and join them by free hand.

∵ Total number of days (n) = 66

Now, $\frac{n}{2}$ = 33

Firstly, we plot a line parallel to X-axis at intersection point of both ogives, which further intersect at (0, 33) on Y- axis. Now, we draw a line perpendicular to X-axis at intersection point of both ogives,

which further intersect at (21.25, 0) on X-axis. Which is the required median using ogives.

Hence, median rainfall = 21.25 cm.

问题9.下表列出了树木的高度：

Daily income (in Rs):	No of workers:
100 – 120	12
120 – 140	14
140 – 160	8
160 – 180	6
180 – 200	10

画“小于”，“大于”。

解决方案：

(i) First we prepare less than frequency table as given below:

Height	Class interval	Frequency	c.f.
Less than 7	0-7	26	26
Less than 14	7-14	31	57
Less than 21	14-21	35	92
Less than 28	21-28	42	134
Less than 35	28-35	82	216
Less than 42	35-42	71	287
Less than 49	42-49	54	341
Less than 56	49-56	19	360

Now we plot the points (7, 26), (14, 57), (21, 92), (28, 134), (35, 216), (42, 287), (49, 341), (56, 360) on the graph and join then in a frequency curve which is ‘less than ogive’

(ii) More than ogive:

First we prepare ‘more than’ frequency table as shown given below:

More than	Class interval	c.f.	Frequency
More than 0	0-7	360	19
More than 7	7-14	341	54
More than 14	14-21	287	71
More than 21	21-28	216	82
More than 28	28-35	134	42
More than 35	35-42	92	35
More than 42	42-49	57	31
More than 49	49-56	26	26
More than 56	56-	0	0

Now we plot the points (0, 360), (7, 341), (14, 287), (21, 216), (28, 134), (35, 92), (42, 57), (49, 26), (56, 0) on the graph and join them in free hand curve to get more than ogive.

问题10.在当地某购物中心的30家商店中赚取的年度利润产生以下分配：

Daily income	Cumulative frequency
Less than 120	12
Less than 140	26
Less than 160	34
Less than 180	40
Less than 200	50

为上述数据绘制两个目标，从而获得中位数。

解决方案：

Class interval	Frequency	c.f.
5-10	3	3
10-15	4	7
15-20	3	10
20-25	4	14
25-30	2	16
30-35	12	28
35-40	2	30

Now plot the points (5, 30), (10, 28), (15, 16), (20, 14), (25, 10), (30, 7) and (35, 3) on the graph and join them to get a more than curve.

Less than curve:

Now plot the points (10, 3), (15, 7), (20, 10), (25, 14), (30, 16), (35, 28) and (40, 30) on the graph and join them to get a less them ogive. The two curved intersect at P. From P, draw PM 1 x-axis, M is the

median which is 22.5

∴ Median = Rs. 22.5 lakh