10类RD Sharma解决方案–第14章坐标几何–练习14.2 |套装3

问题40.证明按顺序取的点(3，0)，(4，5)，(-1，4)和(-2，-1)形成菱形。另外，找到其区域。

解决方案：

Let us considered the given points are A(3, 0), B(4, 5), C(-1, 4) and D(-2, -1)

Now we find the length of the sides and diagonals,

By using distance formula

So, AB = 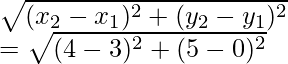$\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(4-3)^2+(5-0)^2}$

AB² = (4 + 3)² + (5 – 0)² 

= (1)² + (5)² 

= 1 + 25 = 26 

Similarly, BC² = (-1 – 4)² + (4 – 5)² 

= (-5)² + (-1)² = 25 + 1 = 26

CD² = (-2 + 1)² + (-1 – 4)²

= (-1)² + (-5)² = 1 + 25 = 26

and DA² = (3 + 2)² + (0 + 1)² 

= (5)² + (1)² = 25 + 1 = 26

Diagonal AC² = (-1 – 3)² + (4 – 0)²

= (-4)² + (4)² = 16 + 16 = 32

and BD² = (-2 – 4)² + (-1 – 5)² 

= (-6)² + (-6)² = 36 + 36 = 72

So, we conclude that the sides AB = BC = CD = DA and diagonal AC is not equal to BD

Hence, ABCD is a rhombus

Now we find the area of rhombus ABCD = Product of diagonals/2

= (√32 × √72)/2 

= (√16 × 2 × 2 × 36)/2

= 4 × 2 × 6/2 

= 24 sq. units

问题41.在教室的课桌座位上，三个学生Rohini，Sandhya和Bina分别坐在A(3、1)，B(6、4)和C(8、6)。您认为他们排成一排吗?

解决方案：

Given that A (3, 1), B (6, 4) and C (8, 6)

Now we find the length of the sides and diagonals,

By using distance formula

AB = 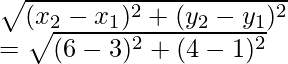$\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(6-3)^2+(4-1)^2}$

AB² = (6 – 3)² + (4 – 1)²

= (3)² + (3)² = 9 + 9 = 18

Similarly, BC² = (8 – 6)² + (6 – 4)²

= (2)² + (2)² = 4 + 4 = 8

and BC² = (8 – 6)² + (6 – 4)² 

= (2)² + (2)² = 4 + 4 = 8 

and CA² = (3 – 8)² + (1 – 6)²

= (-5)² + (-5)² = 25 + 25 = 50

AB = √18 = √9 * 2 = 3√2

BC = √8 = √4 * 2 = 2√2

and CA = √50 = √25 * 2 = 5√2

AB + BC = 3√2 + 2√2 = 5√2 = CA

Hence, A, B and C are collinear points. Hence, they are seated in a line. 

问题42.在y轴上找到一个与点(5，-2)和(-3，2)等距的点。

解决方案：

Let us assume P be the point lies on y-axis. So, its x = 0, so the coordinates of P is (0, y)

It is given that the point P (0, y) is equidistant from the points A(5, -2) and B(-3, 2).

So, PA = PB

Also, PA² = PB²

Now by using distance formula, we get

(5 – 0)² + (-2 – y)² = (-3 – 0)² + (2 – y)²     

25 + 4 + y² + 4y = 9 + 4 – 4y + y²

y² + 4y + 4y – y² = 13 – 29

8y = -16

y = -16/8 = 2

Hence, the required point P is (0,-2)

问题43.找到x和y之间的关系，使点(x，y)与点(3，6)和(-3，4)等距。

解决方案：

Let us considered P (x, y) is equidistant from A(3, 6) and B(-3, 4)

So, PA = PB

Also, PA² = PB²

Now by using distance formula, we get

$\sqrt{(x-3)^2+(y-6)^2}=\sqrt{[x-(-3)]^2+(y-4)^2}\\$

On squaring both sides, we get

(x – 3)² + (y – 6)² = (x + 3)² + (y – 4)²

x² – 6x + 9 + y² – 12y + 36 = x² + 6x + 9 = y² – 8y + 16

-6x – 12y + 45 = 6x – 8y + 25

-6x – 6x – 12y + 8y + 45 – 25 = 0

-12 – 4y + 20 = 0

3x + y – 5 = 0

3x + y = 5

问题44.如果点A(0，2)与点B(3，p)和点C(p，5)等距，则求p的值。

解决方案：

Given that the point A (0, 2) is equidistant from the points B (3, p) and C (p, 5)

Now by using distance formula, we get

 $AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(3-0)^2+(p-2)^2}=\sqrt{(3)^2+p^2-4p+4}\\ =\sqrt{9+p^2-4p+4}=\sqrt{p^2-4p+13}\\ AC =\sqrt{(p-0)^2+(5-2)^2}\\ =\sqrt{p^2+(3)^2}=\sqrt{p^2+9}$

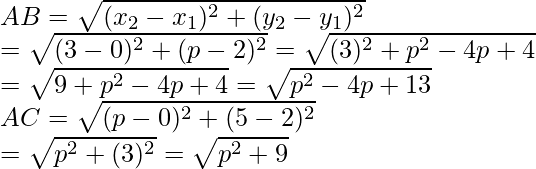
It is given that AB = AC

√p² – 4p + 13 = √p² + 9

So, on squaring both side, we get

= p² – 4p + 13 = p² + 9

p² – 4p – p² = 9 – 13

-4p = -4

p = 1

Hence, the value of p is 1

问题45.证明点(7、10)，(-2、5)和(3，-4)是等腰直角三角形的顶点。

解决方案：

Let us considered the points are A (7, 10), B (-2, 5) and C (3, -4)

Now we find the length of the sides 

By using distance formula

Now AB = 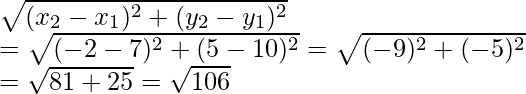$\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(-2-7)^2+(5-10)^2}=\sqrt{(-9)^2+(-5)^2}\\ =\sqrt{81+25}=\sqrt{106}$

Similarly, BC = $\sqrt{(3+2)^2+(-4-5)^2}=\sqrt{106}$

and AC = $\sqrt{(3-7)^2+(-4-10)^2}=\sqrt{212}$

So, we conclude that AB = BC = √106 and AB² + BC² = AC²

Hence, ABC is an isosceles right triangle

问题46.如果点P(x，3)与点A(7，-1)和点B(6，8)等距，则求出x和And的值。

解决方案：

It is given that Point P (x, 3) is equidistant from the points A (7, -1) and B (6, 8)

So, PA = PB

$\sqrt{(x-7)^2+(3+1)^2}=\sqrt{(x-6)^2+(3-8)^2}$

On squaring both sides, we get

(x – 7)² + (4)² = (x – 6)² + (-5)²

x² – 14x + 49 + 16 = x² – 12x + 36 + 25

x² – 14x + 65 = x² – 12x + 61

x² – 14x + 12x – x² = 61 – 65

-2x = -4

x = -4/-2 = 2

x = 2

Now we find the distance $AP=\sqrt{(2-7)^2+(4)^2}=\sqrt{(-5)^2+(4)^2} = \sqrt{41}$

问题47.如果A(3，y)与点P(8，-3)和Q(7，6)等距，则求y的值并求出距离AQ。

解决方案：

It is given that point A (3, y) is equidistant from P (8, -3) and Q (7, 6)

So, AP = AQ

$\sqrt{(3-8)^2+(y+3)^2} = \sqrt{(3-7)^2+(y-6)^2}$

On squaring both sides, we get

(3 – 8)² + (y + 3)² = (-4)² + (y – 6)²

(-5)² + y² + 6y + 9 = 16 + y² – 12y + 36

25 + y² + 6y + 9 = 16 + y² – 12y + 36

y² + 6y – y² + 12y = 36 – 9 – 25 + 16

18y = 18

y = 18/18 = 1

y = 1

Now we find the distance 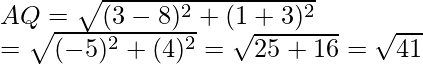$AQ=\sqrt{(3-8)^2+(1+3)^2}\\ =\sqrt{(-5)^2+(4)^2}=\sqrt{25+16}=\sqrt{41}$

问题48.如果(0，-3)和(0，3)是等边三角形的两个顶点，请找到其第三个顶点的坐标。

解决方案：

Given that the A (0, -3) and B (0, 3) are the two vertices of an equilateral triangle ABC

Let us assume that the coordinates of the third vertex be C (x, y)

In equilateral triangle, AC = AB

So,

(x – 0)² + (y + 3)² = (0 – 0)² + (3 + 3)²

x² + (y + 3)² = 0 + (6)² = 36

x² + y² + 6y + 9 = 36

x² + y² + 6y = 36 – 9 = 27              …….(i)

Also, BC = AB 

(x – 0)² + (y – 3)² = 36

x² + y² + 9 – 6y = 36

x² + y² – 6y = 36 – 9 = 27              ……..(ii)

So, from eq (i) and (ii), we get

x² + y² + 6y = x² + y² – 6y

x² + y² + 6y – x² – y² + 6y = 0

12y = 0

y = 0

Now put the value of y in eq(i)

x² + y² + 6y = 27

x² + 0 + 0 = 27

x = ±√27 = ±3√3

So, the coordinates of third point is(3√3, 0) or (-3√3, 0) 

问题49.如果点P(2，2)与点A(-2，k)和点B(-2k，-3)等距，则找到k。另外，找到AP的长度。

解决方案：

Given that the point P (2, 2) is equidistant from the points A (-2, k) and B (-2k, -3)

So, AP = BP

(2 + 2)² + (2 – k)² = (2 + 2k)² + (2 + 3)²

(4)² + (2 – k)² = (2 + 2k)² + (5)²

16 + 4 + k² – 4k = 4 + 4k² + 8k + 25

4k² + 8k + 29 – 16 – 4 – k² + 4k = 0

3k² + 12k + 9 = 0

k² + 4k + 3 = 0

k² + k + 3k + 3 = 0

k(k + 1) + 3(k + 1) = 0

(k + 1)(k + 3) = 0

So, the value of k either k + 1 = 0, then k = -1

or k + 3 = 0, then k = -3

Therefore, k = -1, -3

Now we find the distance 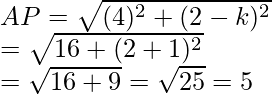$AP=\sqrt{(4)^2+(2-k)^2}\\ =\sqrt{16+(2+1)^2}\\ =\sqrt{16+9}=\sqrt{25}=5$

问题50.显示∆ABC，其中A(-2，0)，B(2，0)，C(0，2)和∆PQR，其中P(-4，0)，Q(4，0)， R(0，4)相似。

解决方案：

Given that In ∆ABC, the vertices are A (-2, 0), B (2, 0), C (0, 2) 

In ∆PQR, the vertices are P (-4, 0), Q (4, 0), R (0, 4)

Show that ∆ABC ~ ∆PQR

So, 

$AB=\sqrt{(2+2)^2+(0-0)^2}\\ =\sqrt{16}=4\\ BC=\sqrt{(0-2)^2+(2-0)^2}\\ =\sqrt{4+4}=\sqrt{8}=2\sqrt{2}$

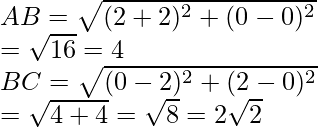
Now, 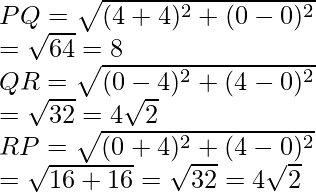$PQ=\sqrt{(4+4)^2+(0-0)^2}\\ =\sqrt{64}=8\\ QR=\sqrt{(0-4)^2+(4-0)^2}\\ =\sqrt{32}=4\sqrt{2}\\ RP=\sqrt{(0+4)^2+(4-0)^2}\\ =\sqrt{16+16}=\sqrt{32}=4\sqrt{2}$

So, AB/PQ = 4/8 = 1/2

BC/QR = 2√2/4√2  = 1/2

CA/PQ = 2√2/4√2 = 1/2 

So, AB/PQ = BC/QR = CA/RP

By using SSS

∆ABC ~ ∆PQR  

问题51.等边三角形在点(3，4)和(-2，3)处有两个顶点。找到第三个顶点的坐标。

解决方案：

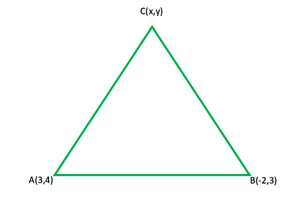
Given that the A (3, 4) and B (-2, 3) are the two vertices of an equilateral triangle ABC

Let us assume that the coordinates of the third vertex be C (x, y)

Now 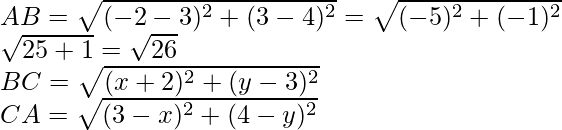$AB=\sqrt{(-2-3)^2+(3-4)^2}=\sqrt{(-5)^2+(-1)^2}\\ \sqrt{25+1}=\sqrt{26}\\ BC=\sqrt{(x+2)^2+(y-3)^2}\\ CA=\sqrt{(3-x)^2+(4-y)^2}$

As we know that in equilateral triangle, AB = BC = CA

So, BC = AB

$\sqrt{(x+2)^2+(y-3)^2}=\sqrt{26}$

On squaring both side we get

(x + 2)² + (y – 3)² = 26

x² + 4x + 4 + y² – 6y + 9 = 26

x² + y² + 4x – 6y + 13 = 26

x² + y² + 4x – 6y = 26 – 13 = 12     ………..(i) 

Similarly, CA = AB 

$\sqrt{(3-x)^2+(4-y)^2}=\sqrt{26}$

On squaring both side we get

(3 – x)² + (4 – y)² = 26

9 + x² – 6x + 16 + y² – 8y = 26

x² + y² – 6x – 8y + 25 = 26

x² + y² – 6x – 8y = 26 – 25 = 1             …….(ii)

Now on subtracting eq(ii) from (i), we get

10x + 2y = 12

5x + y = 6                        ……..(iii)

y = 6 – 5x

Now substituting the value of y in eq(i), we get

x² + (6 – 5x)² + 4x – 6(6 – 5x) = 13

x² + 36 + 25x² – 60x + 4x – 36 +  30x – 13 = 0

26x² – 26x – 13 = 0

2x² – 2x – 1 = 0

Here, a = 2, b = -2, c = -1

$x=\frac{-b±\sqrt{b^2-4ac}}{2a}\\ =\frac{-(-2)±\sqrt{(-2)^2-4\times 2\times (-1)}}{2\times 2}\\ =\frac{2±\sqrt{4+8}}{4}\\ =\frac{2±\sqrt{12}}{4}\\=\frac{2±2\sqrt{3}}{4}=\frac{1±\sqrt{3}}{2}$

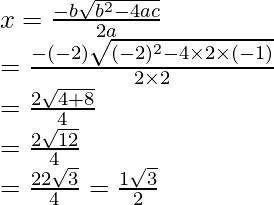
 When x = (1 + √3)/2, then y = 6 – 5x = 6 – 5((1 + √3)/2) = (7 – 5√3)/2

Or when x = (1 – √3)/2, then y = 6 – 5x = 6 – 5((1 – √3)/2) = (7 + 5√3)/2

Hence, the co-ordinates of the point C is ((1 + √3)/2, (7 – 5√3)/2) or ((1 – √3)/2, (7 + 5√3)/2)

问题52.找到顶点为(-2，-3)，(-1、0)，(7，-6)的三角形的外接心。

解决方案：

Given that the vertices of ∆ABC are A(-2, -3), B(-1, 0), and C(7, -6), and 

let us assume that O is the circumcenter ∆ABC. So, the coordinates of O will be (x, y)

So, OA = OB = OC 

Or OA² = OB² = OC²

Now $OA = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

OA² = (x + 2)² + (y + 3)²

= x² + 4x + 4 + y² + 6y + 9

= x² + y² + 4x + 6y + 13

OB² = (x + 1)² + (y + 0)²

= x² + 2x + 1 + y²

= x² + y² + 2x + 1

OC² = (x – 7)² + (y + 6)²

= x² – 14x + 49 + y² + 12y + 36

= x² + y² – 14x + 12y + 85

OA² = OB²

x² + y² + 4x + 6y + 13 = x² + y² + 2x + 1

4x + 6y -2y = 1 – 13

2x + 6y = -12

x + 3y = -6       ………(i)

OB² = OC²

x² + y² + 2x + 1 = x² + y² – 14x + 12y + 85

2x + 14x – 2y = 85 – 1

16x – 12y = 84

4x – 3y = 21              ………(ii)   

From eq (i), we get

x = -3y – 6

On substituting the value of x in eq (ii)

4(-3y – 6) – 3y = 21

-12 – 24 – 3y = 21

-15y = 21 + 24

-15y = 45

y = -45/15 = -3 

x = -3y – 6 = -3 × (-3) – 6

= + 9 – 6 = 3

Hence, the co-ordinates of O are (3,-3)

问题53.找到端点为(0，100)和(10，0)的线段在原点处所成的角度。

解决方案：

Let us considered the co-ordinates of the end points of a line segment are 

A (0, 100), B (10, 0) and origin is O (0, 0)

So, the angle subtended by the line PQ at the origin is 90° or π/2

问题54.找到通过(5，-8)，(2，-9)和(2，1)的圆的中心。

解决方案：

Given that O is the centre of the circle and A(5, -8), B(2, -9), and C (2, 1) are the points on the circle.

So, let us considered the co-ordinates of O be (x, y)

Therefore, OA = OB = OC               

OA² = OB² = OC²

Now $OA=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

OA² = (x – 5)² + (y + 8)²

= x² – 10x + 25 + y² + 16y + 64

= x² + y² – 10x + 16y + 89

Similarly, OB² = (x – 5)² + (y + 9)²

= x² + 4 – 4x + y² + 81 + 18y

= x² + y² – 4x + 18y + 85

and OC² = x² – 4x + 4 + y² – 2y + 1

= x² + y² – 4x – 2y + 5

OA² = OB²

x² + y² – 10x + 16y + 89 = x² + y² – 4x + 18y + 85

-10x + 4x + 16y – 18y = 85 – 89

-6x – 2y = -4               

3x + y = 2                         …….(i)

OB² = OC²

x² + y² – 4x + 18y + 85 = x² + y² – 4x – 2y + 5

18y + 2y = 5 – 85

20y = -80

y = -80/10 = -4

Now substitute the value of y in eq(i), we get

3x + y = 2

3x – 4 = 2

3x = 2 + 4 = 6

x = 6/3 = 2

Hence, the co-ordinates of O are(2,-4)

问题55.如果一个正方形的两个相对顶点分别是(5，4)和(1，-6)，则求出其其余两个顶点的坐标。

解决方案：

Given that the two opposite points of a ABCD square are A(5, 4) and C(1, -6)

Let us considered that the co-ordinates of B be (x, y). 

So, join AC

As we know that the sides of a square are equal, so,

AB = BC                   

AB² = BC²

(x – 5)² + (y – 4)² = (x – 1)² + (y + 6)²

x² – 10x + 25 + y² – 8y + 16 = x² – 2x + 1 +y² + 12y + 36

-10x + 2x – 8y – 12y = 37 – 41

-8x – 20y = -4                  

2x + 5y = 1

2x = 1 – 5y

x = (1 – 5y)/2

So, ABC is a right-angled triangle 

Now by using Pythagoras theorem, we get

AC² = AB² + BC²

(5 – 1)² + (4 + 6)² = x² – 10x + 25 + y² – 8y + 16 + x² – 2x + 1 + y² + 12y + 36

(4)² + (10)² = 2x² + 2y² – 12x + 4y + 78

16 + 100 = 2x² + 2y² – 12x + 4y + 78

2x² + 2y² – 12x + 4y + 78 – 16 – 100 = 0

2x² + 2y² – 12x + 4y – 38 = 0

x² + y² – 6x + 2y – 19 = 0     …..(i)            

Now substituting x = (1 – 5y)/2 in eq(i), we get

$(\frac{1-5y}{2})^2+y^2-6(\frac{1-5y}{2})+2y-19=0\\ \frac{1+25y^2-10y}{4}+y^2-3(1-5y)+2y-19=0$

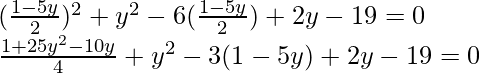
1 + 25y² – 10y + 4y² – 12 + 60y + 8y – 76 = 0

29y² + 58y – 87 = 0

y² + 2y – 3 = 0

y² + 3y – y – 3 = 0

y(y + 3) – 1(y + 3) = 0

(y + 3)(y – 1) = 0

The value of y can be either y + 3 = 0, then y = -3

or y – 1 = 0, then y = 1

When y = 1, then

x = (1 – 5y)/2

= (1 – 5(1))/2

= -2 

When y = -3, then

x = (1 – 5(-3))/2

= 8

So, the other points of ABCD square are(-2,1) and (8,-3)

问题56.找到通过(6，-6)，(3，-7)和(3，3)的圆的中心。

解决方案：

Let us considered O be the centre of the circle is (x, y) 

It is given that centre of the circle passing through (6, -6), (3, -7), and (3, 3)

Join OA, OB and OC

So, OA = OB = OC         

OA² = (x -6 )² + (y + 6)² 

OB² = (x – 3)² + (y + 7)²        

and OC² = (x – 3)² + (y-3)²

As we know that OA² = OB²

So, (x – 6)² + (y + 6)² = (x – 3)² + (y + 7)²

x² – 12x + 36 + y²+12y + 36 = x² – 6x + 9 + y² + 14y + 49

x² – 12x + 36 + y²+12y + 36 – x² + 6x – 9 – y² – 14y – 49 = 0

-12x + 12y + 72 + 6x – 14y – 58 = 0

-6x – 2y + 14 = 0

-6x – 2y = -14

3x + y = 7                 …..(i)

Also, OB² = OC²

(x – 3)² + (y + 7)² = (x – 3)² + (y – 3)²

x² – 6x + 9 + y²+ 14y + 49 = x² – 6x + 9 + y² – 6y + 9

x² + y² – 6x + 58 + 14y – x² – y² + 6x + 6y – 18 = 0

20y + 40 = 0

20y = -40

y = -40/20 = -2

3x + (-2) = 7

3x = 7 + 2 = 9

x = 9/3 = 3

Hence, the co-ordinates of the centre are(3,-2)

问题57.正方形的两个相对顶点是(-1，2)和(3，2)。查找其他两个顶点的坐标。

解决方案：

Let us considered ABCD is square, in which the co-ordinates are A (-1, 2) and C (3, 2).

Let us assume the coordinates of B are (x, y)

Now, join AC

As we know that the sides of a square are equal, so,

AB = BC                        

AB² = BC²

Now 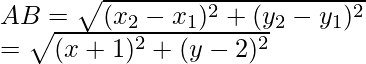$AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(x+1)^2+(y-2)^2}$

AB² = (x + 1)² + (y – 2)²

Similarly, BC² = (x – 3)² + (y – 2)²

As we know that AB = BC

So, 

(x + 1)² + (y – 2)² = (x – 3)² + (y – 2)²

(x + 1)² = (x – 3)²

x² + 2x + 1 = x² – 6x + 9

x² + 2x + 6x – x² = 9 – 1 = 8

8x = 8

x = 8/8 = 1

Now in right triangle ABC

AC² = AB² + BC²

(3 + 1)² + (2 – 2)² = (x + 1)² + (y – 2)² + (x – 3)² + (y – 2)²

(4)² + (0)² = x² + 2x + 1 + y² – 4y + 4 + x² – 6x + 9 + y² – 4y + 4 

16 = 2x² + 2y² – 4x – 8y + 18

2x² + 2y² – 4x – 8y = 16 – 18

2x² + 2y² – 4x – 8y = -2

x² + y² – 2x – 4y = -1    …….(i)

Now substitute the value of x, in eq(i), we get

(1)² + y² – 2 × 1 – 4y = -1

1 + y² – 2 – 4y = -1

y² – 4y = -1 – 1 + 2 = 0

y(y – 4) = 0

So the value of the y can be either y = 0

or y – 4 = 0, then y = 4

Hence, the coordinates of other points will be (1, 0) and (1, 4)