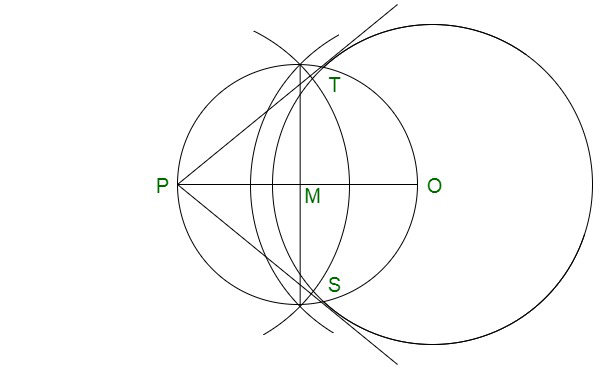
问题1.画一个半径为6厘米的圆。从距中心10厘米的点开始,构造与圆的切线对,并测量其长度。
解决方案:
Follow these steps for construction :
Step 1: Construct of 6 cm radius with centre O.
Step 2: Mark a point P, 10 cm away from the centre O.
Step 3: Now join PO then bisect it at M.
Step 4: From the centre M and the diameter PO, construct a circle that will be intersecting the given circle at T and S.
Step 5: Thus join PT and PS.
Further PT and PS are the required tangents.
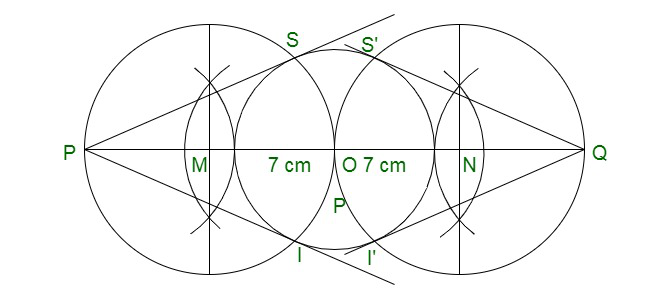
问题2.画一个半径为3厘米的圆。在其延伸直径之一上取两个点P和Q,每个点距其中心7厘米。从这两个点P和Q向圆画切线。
解决方案:
Follow these steps for construction :
Step 1: Construct of radius 3 cm with the centre O.
Step 2: Construct a diameter.
Step 3: Mark two points P and Q on this diameter with a distance of 7 cm each from the centre O, as shown below.
Step 4: Now bisect QO at N and PO at M.
Step 5: From the centres M and N, construct circle on ‘PO’ and ‘QO’ as diameter which intersect the given circle at S, T and S’, T’ respectively.
Step 6: Further join PS, PT, QS’ and QT’.
Therefore, PS, PT, QS’ and QT’ are the required tangents to the given circle.
问题3.画一条长度为8厘米的线段AB。以A为中心,绘制一个半径为4厘米的圆,以B为中心,绘制另一个半径为3厘米的圆。从另一个圆的中心到每个圆的切线。 [CBSE 2013]
解决方案:
Follow these steps for construction:
Step 1: Construct a line segment AB of 8 cm.
Step 2: Draw circles from the centre A and radius 4 cm and with centre B and radius 3 cm.
Step 3: Now bisect AB at M.
Step 4: From centre M and diameter AB, construct a circle which will intersects the two circles at S’, T’ and S, T respectively.
Step 5: Further join AS, AT, BS’and BT’.
Therefore, AS, AT, BS’ and BT’ are the required tangent.

问题4.在距点P中心6.2 cm的距离P处的半径3.5 cm的圆上绘制两个切线。
解决方案:
Follow these steps for construction :
Step 1: Construct a circle of radius 3.5 cm with centre O.
Step 2: Mark a point P which will be of 6.2 cm from O.
Step 3: Now bisect PO at M and construct a circle with centre M and diameter OP which will intersects the given circle at T and S respectively.
Step 4: Further join PT and PS.
Therefore, PT and PS are the required tangents to circle.

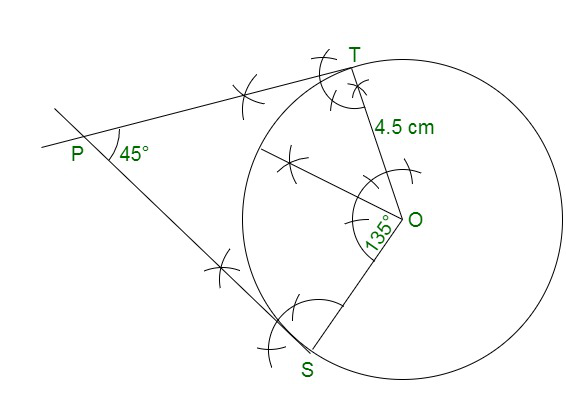
问题5.在半径为4.5 cm的圆上绘制一对切线,这些切线以45°的角度彼此倾斜。 [CBSE 2013]
解决方案:
Follow these steps for construction:
At centre the angle is 180° – 45° = 135°
Step 1: Construct a circle of radius 4.5 cm with centre O.
Step 2; Now, at O, construct an angle ∠TOS = 135°
Step 3: Further at T and S draw perpendicular which will meet at P.
Therefore, PT and PS are the tangents which inclined each other 45°.
问题6.画一个直角三角形ABC,其中AB = 6 cm,BC = 8 cm,andB = 90°。在AC上从B垂直绘制BD,并绘制一个穿过点B,C和D的圆。构造从A到该圆的切线。
解决方案:
Follow these steps for construction:
Step 1: Construct a line segment BC of 8 cm
Step 2: From B construct an angle of 90°
Step 3: Construct an arc BA˘ of 6cm cutting the angle at A.
Step 4: Now join AC. Thus, ΔABC is the required A.
Step 5: Construct perpendicular bisector of BC cutting BC at M.
Step 6: Mark M as centre and BM as radius, construct a circle.
Step 7: Mark A as centre and AB as radius, construct an arc cutting the circle at E. Thus, join AE.
Therefore, AB and AE are the required tangents.
Justification:
Given: ∠ABC = 90°
Thus, OB is a radius of the circle.
Therefore, AB is a tangent to the circle.
Also AE is a tangent to the circle.

问题7.画出两个半径分别为3 cm和5 cm的同心圆。从较大圆上的点构造与较小圆的切线。另外,测量其长度。 [CBSE 2016]
解决方案:
Given: Two concentric circles of radii 3 cm and 5 cm with centre O.
We have to construct a pair of tangents from point P on outer circle to the other.
Follow these steps for construction:
Step 1: Construct two concentric circles of radii 3 cm and 5 cm with the centre O.
Step 2: Then, take any point P on outer circle and join OP.
Step 3: Now, bisect OP and let M’ be the mid-point of OP.
Take M’ as centre and OM’ as radius construct a circle dotted which will cut the inner circle as M and P’.
Step 4: Further, join PM and PP’. Therefore, PM and PP’ are the required tangents.
Step 5: After measuring PM and PP’, we find that PM = PP’ = 4 cm.
Actual calculation:
In right angle ΔOMP, ∠PMO = 90°
Therefore,
PM2 = OP2 – OM2 {by Pythagoras theorem i.e. (hypotenuse)2 = (base)2 + (perpendicular)2}
⇒ PM2 = (5)2 – (3)2 = 25 – 9 = 16
⇒ PM = 4 cm
Hence, the length of both tangents is 4 cm.
