第 10 类 RD Sharma 解决方案 - 第 11 章构造 - 练习 11.2 |设置 2

问题 11. 构造一个与给定 ΔXYZ 相似的三角形，其边等于 ΔXYZ 对应边的 (3/2) ^th 。写出施工步骤。

解决方案：

Follow these steps for the construction:

Step 1: Construct a triangle XYZ along some feasible data.

Step 2: Construct a ray YL creating an acute angle along XZ and break off 5 equal parts creating 

YY₁= Y₁Y₂ = Y₂Y₃ = Y₃Y₄.

Step 3: Connect Y₄ and Z.

Step 4: From Y₃, construct Y₃Z’ parallel to Y₄Z and Z’X’ parallel to ZX.

Therefore,

We have the required triangle ΔX’YZ’.

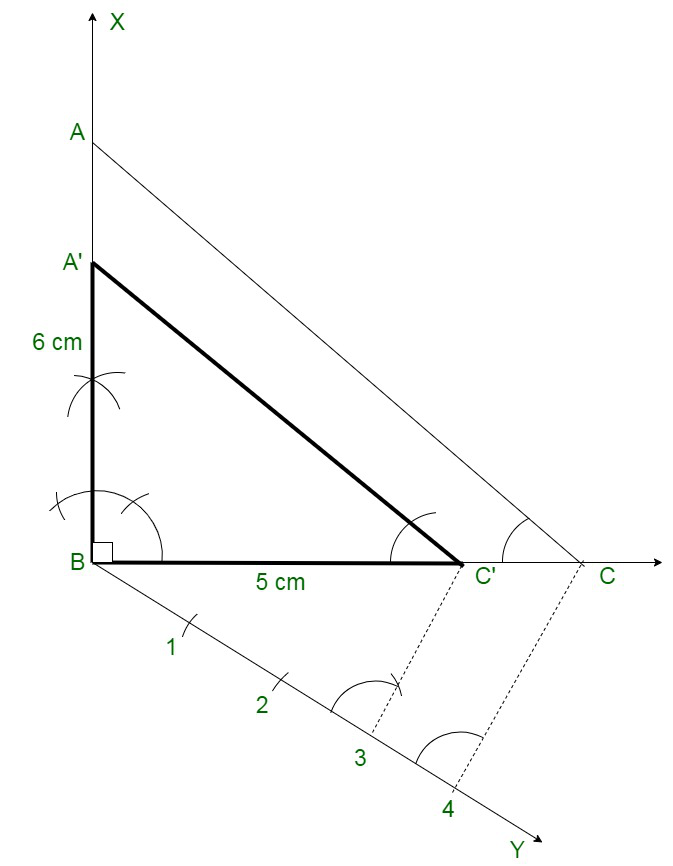
问题 12. 画一个直角三角形，其中边（斜边除外）的长度分别为 8 厘米和 6 厘米。然后构造另一个三角形，其边是第一个三角形对应边的 3/4 倍。

解决方案：

Follow these steps for the construction

Step 1: Construct right ΔABC right angle at B and BC of 8 cm and BA of 6 cm.

Step 2: Construct a line BY creating a cut angle along BC and break off 4 equal parts.

Step 3: Connect 4C and Construct 3C’ || 4C and C’A’ parallel to CA.

Therefore,

We have the required triangle ΔBC’A’ is the required triangle.

问题 13. 构造一个边长为 5 厘米、5.5 厘米和 6.5 厘米的三角形。现在构造另一个三角形，其边是给定三角形对应边的 3/5 倍。

解决方案：

Follow these steps for the construction:

Step 1: Construct a line segment BC of 5.5 cm.

Step 2: Along centre B and radius 5 cm and along centre C and radius 6.5 cm, 

Construct arcs that bisect each other at A

Step 3: Connect BA and CA. ΔABC is the given triangle.

Step 4: At B, construct a ray BX creating an acute angle and break off 5 equal parts from BX.

Step 5: Connect C5 and Construct 3D || 5C which connects BC at D.

From D, construct DE || CA which meets AB at E.

Therefore,

We have the required triangle ΔEBD.

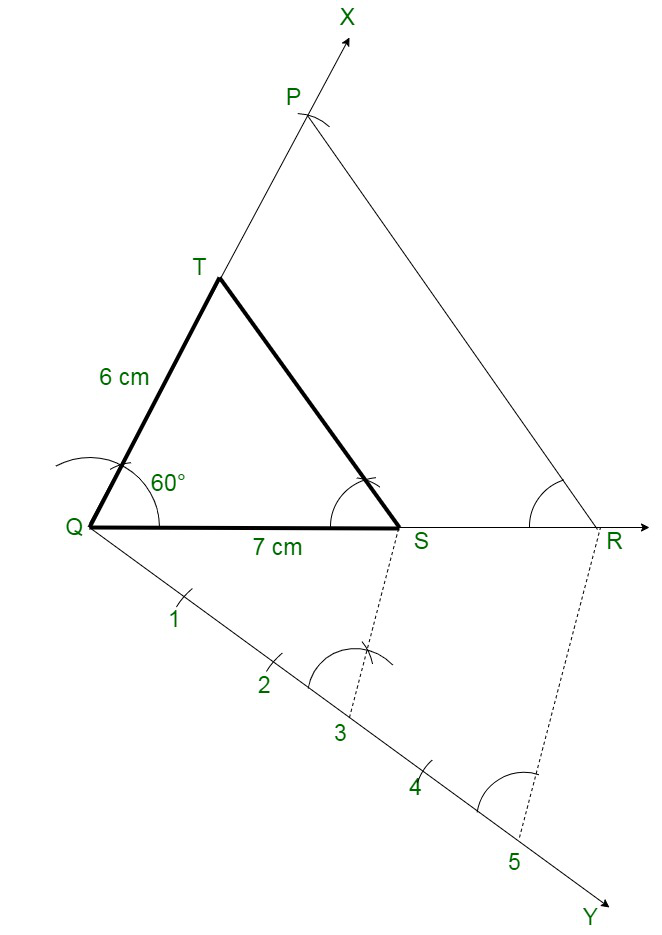
问题 14. 构造一个三角形 PQR，边长 QR = 7 cm，PQ = 6 cm，∠PQR = 60°。然后构造另一个三角形，其边是 ΔPQR 对应边的 3/5。

解决方案：

Follow these steps for the construction:

Step 1: Construct a line segment QR = 7 cm.

Step 2: At Q construct a ray QX creating an angle of 60° and cut of PQ = 6 cm. 

Connect PR.

Step 3: Construct a ray QY creating an acute angle and break off 5 equal parts.

Step 4: Connect 5, R and through 3, construct 3, S parallel to 5, R which meet QR at S.

Step 5: Through S, construct ST || RP meeting PQ at T.

Therefore,

We have the required ΔQST.

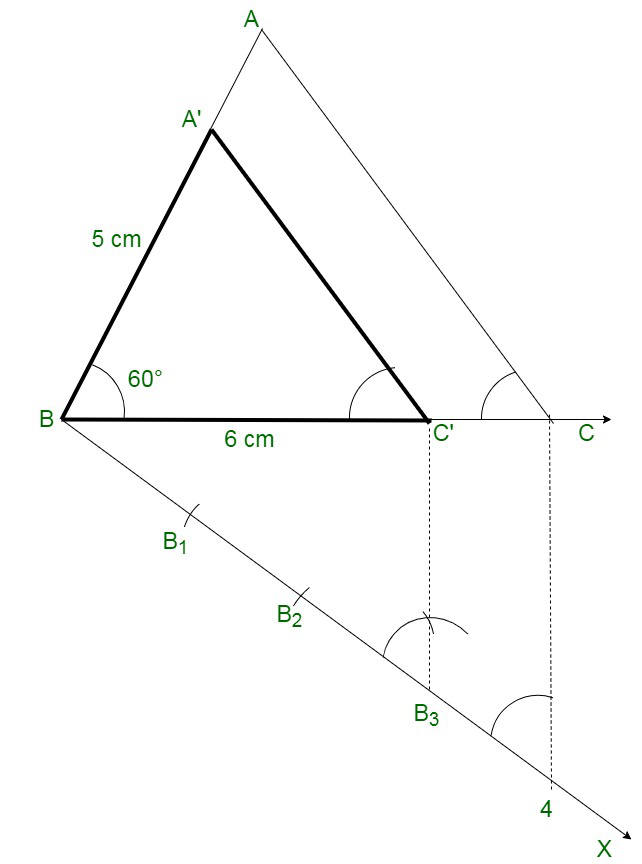
问题 15. 构造一个 ΔABC，其中底边 BC = 6 cm，AB = 5 cm，∠ABC = 60°。然后构造另一个三角形，其边是 ΔABC 对应边的 3/4。

解决方案：

Follow these steps for the construction:

Step 1: To construct a triangle ABC 

Along side of BC of 6 cm, 

AB of 5 cm and ∠ABC = 60°.

Step 2: Construct a ray BX, which creates an acute angle ∠CBX below the line BC.

Step 4: Make four points B₁, B₂, B₃ and B₄ on BX such that BB₁ = B₁B₂  = B₂B₃ = B₃B₄.

Step 5: Connect B₄C and construct a line through B₃ parallel to B₄C bisecting BC to C’.

Step 6: Construct a line through C’ parallel to the line CA to intersect BA at A’.

Therefore,

We have the required triangle ΔABC.

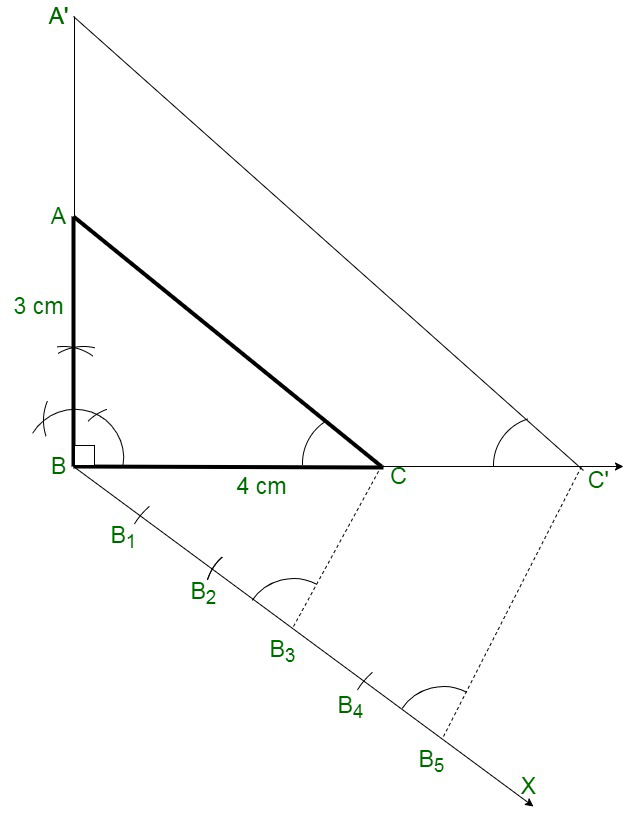
问题 16. 构造一个直角三角形，其中边（斜边除外）的弧长分别为 4 厘米和 3 厘米。现在，构造另一个三角形，其边是给定三角形对应边的 5/3 倍。

解决方案：

Follow these steps for the construction:

Step 1: Construct a right triangle ABC in which the sides (other than the hypotenuse) are 

of lengths 4 cm and 3 cm. ∠B = 90°.

Step 2: Construct a line BX, that creates an acute angle ∠CBX below the line BC.

Step 3: Mark 5 points B₁, B2₂, B₃, B₄ and B₅ on BX such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅.

Step 4: Connect B₃ to C and Construct a line through B₅ parallel to B₃C, 

bisecting the extended line segment BC at C’.

Step 5: Construct a line through C’ parallel to CA bisecting the extended line segment BA at A’.

Therefore,

We have the required triangle ΔA’BC’.

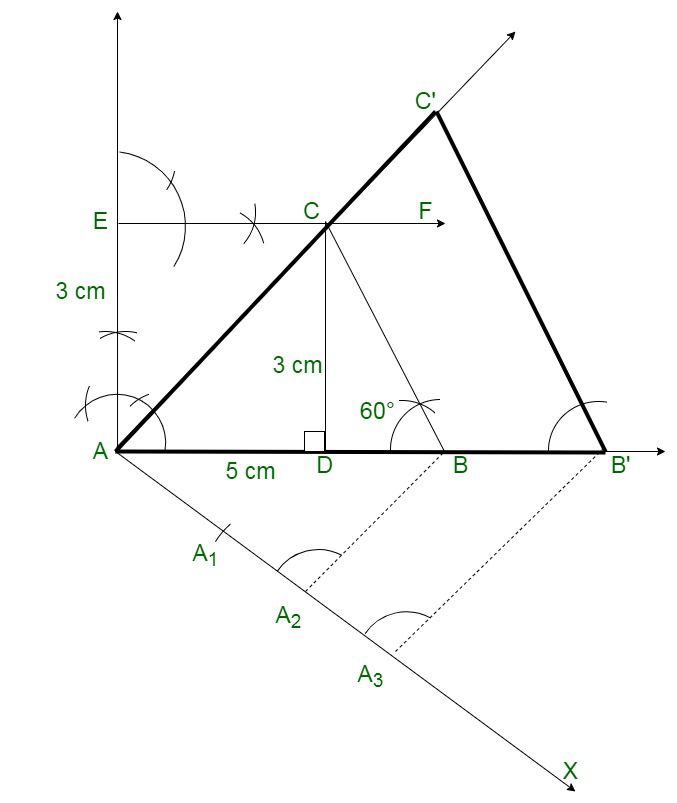
问题 17. 构造一个 ΔABC，其中 AB = 5 cm，∠B = 60°，高度 CD = 3 cm。构造一个类似于 ΔABC 的 ΔAQR，使得 ΔAQR 的边是 ΔACB 对应边的 1.5 倍。

解决方案：

Follow these steps for the construction:

Step 1: Construct a line segment AB of 5 cm.

Step 2: At A, construct a perpendicular and break off AE = 3 cm.

Step 3: From E, construct EF || AB.

Step 4: From B, construct a ray creating an angle of 60 meeting EF at C.

Step 5: Connect CA. After that ABC is the triangle.

Step 6: From A, construct a ray AX creating an acute angle along AB and break 

off 3 equal parts creating AA₁ = A₁A₂ = A₂A₃.

Step 7: Connect A₂ and B.

Step 8: From A , construct A^B’ parallel to A₂B and B’C’ parallel to BC.

Therefore,

We have the required triangle ΔC’AB’.