10类RD Sharma解决方案–第4章三角形–练习4.5 |套装2

问题13：两个相似的三角形的周长分别为25厘米和15厘米。如果第一个三角形的一侧是9厘米，那么另一个三角形的对应侧是什么?

解决方案：

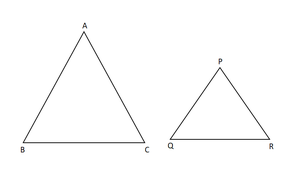
Given: perimeter of two similar triangles are 25 cm, 15 cm and one side 9 cm

To find : the other side.

Let the two triangles be ABC & PQR.

Let one of its side is (AB) = 9 cm and the other side of other triangle be PQ.

∆ABC ∼ ∆PQR.      [Since the ratio of corresponding sides of similar triangles is same as the ratio of their perimeters.]

AB/PQ = BC/QR = AC/PR = 25/15

9/PQ = 25/15

25 PQ = 15 × 9

PQ = (15×9)/25

PQ =(3× 9 )/5

PQ = 27/5

PQ =  5.4 cm

Hence, the corresponding side of other ∆ is 5.4 cm.

问题14.在ΔABC和ΔDEF中，假设AB = 5 cm，BC = 4 cm，CA = 4.2 cm，DE = 10 cm，EF = 8 cm，FD = 8.4 cm。如果AL⊥BC，DM⊥EF，则找到AL：Dm。

解决方案：

Given,

AB = 5 cm, BC = 4 cm, CA = 4.2 cm, DE = 10 cm, EF = 8 cm, and FD = 8.4 cm

AL ⊥ BC, DM ⊥ EF

To find: AL: DM

Now In ∆ABC and ∆DEF,

AB/DE=BC/EF=AC/DF=1/2   [both triangles are similar]

[In similar triangle the ratio of corresponding altitude is same as the ratio of the corresponding sides.]

$\therefore$   AL: DM = 1: 2

问题15. D和E分别是ΔABC的AB和AC侧的点，使得AD = 8 cm，DB = 12 cm，AE = 6 cm和CE = 9 cm。证明BC = 5/2 DE。

解决方案：

AE/EC=6/9=2/3…….(1)

AD/DB=8/12=2/3……(2)

from (1) and (2) we know that 

$\therefore$AD/DB=AE/EC

$\therefore$ ED∥CB                                                

Now In△AED and △ACB,

 ED∥CB  

∠AED=∠ACB

∠ADE=∠ABC

△AED∼△ACB    [by AAA criteria]

$\therefore$ AE/AC=ED//CB

AE/EC+AE= ED/CB [$\therefore$AC=AE+EC]

6/6+9= ED/CB

6/15=2/5=ED/CB

$\therefore$CB=5/2ED  

 Hence proved

问题16. D是ΔABC边BC的中点。 AD在E点被一分为二，生成的BE在X点被切掉AC。证明BE：EX = 3：1

解决方案：

Given: In ∆ABC, D is the midpoint of BC, E is the midpoint of AD. BE produced meets AC at X.

To prove :  BE: EX = 3 : 1

Now In Δ BCX  and  ΔDCY,

∠CBX  = ΔCBY   (corresponding angles)

∠CXB  = ΔCYD   (corresponding angles)

$\therefore$ΔBCX∼ΔDCY   (AA similarity)

$\therefore$BC/DC = BX/ DY = CX/CY    [ corresponding sides of two similar triangles are proportional]

BX/DY = BC/DC

BX/DY = 2DC/DC   [As D is the midpoint of BC]

BX/DY = 2/1…………(i)

Now In ΔAEX and ΔADY,

∠AEX  = ΔADY   (corresponding angles)

∠AXE = ΔAYD   (corresponding angles)

$\therefore$ΔAEX ∼ ΔADY   (AA similarity)

$\therefore$AE/AD = EX/DY = AX/AY  [ corresponding sides of two similar triangles are proportional]

EX/DY = AE/AD

EX/DY = AE/2AE                 [ D is the midpoint of BC]

EX/DY = ½…………..…(ii)

On Dividing eqn. (i) by eqn. (ii) we get,

BX/EX = 4/1

BX = 4EX

BE + EX = 4EX

BE = 4EX – EX

BE = 3EX

BE /EX = 3/1

BE : EX = 3:1

Hence proved

问题17. ABCD是平行四边形，APQ是在P处与BC在Q处相交的直线。证明BP和DQ所获得的矩形等于AB和BC所包含的矩形。

解决方案：

Given : ABCD is a parallelogram and APQ is a straight line meeting BC at P and DC produced at Q.

To prove : BP x DQ = AB x BC

Now In ∆ABP and ∆QDA,

∠B = ∠D [Opposite angles of parallelogram]

∠BAP = ∠AQD [Alternate interior angles]

$\therefore$ ∆ABP ~ ∆QDA [By AA similarity]

$\therefore$AB/QD = BP/DA   [the corresponding sides of similar triangles are proportional]

DA = BC  [opposite sides of a parallelogram are equal]

AB/QD = BP/BC

AB × BC = QD × BP

Hence proved

问题18：在ΔABC中，AL和CM是从顶点A和C到BC和AB的垂线。如果Al和CM在O相交，则证明：

(i)ΔOMA〜ΔOLC

(ii)OA / OC = OM / OL

解决方案：

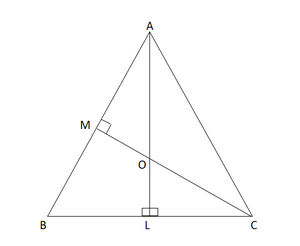
Given,

AL ⊥ BC and CM ⊥ AB

To prove:

(i)  ΔOMA ∼ ΔOLC

(ii)OA/OC=OM/OL

Now In Δ OMA and ΔOLC,

∠MOA = ∠LOC                [Vertically opposite angles]

∠AMO = ∠CLO                [Each 90°]

$\therefore$ΔOMA ~ ΔOLC       [By AA similarity]

$\therefore$OA/OC=OM/OL  [Corresponding parts of similar Δ are proportional]

Hence proved

问题19. ABCD是四边形，其中AD = BC。如果P，Q，R，S是AB，AC，CD和BD方面的中点。证明PQRS是菱形。

解决方案：

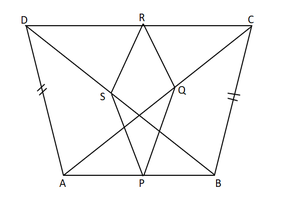
Given, 

ABCD is a quadrilateral in which AD = BC and P, Q, R, S are the mid points of AB, AC, CD, BD, respectively.

To prove: PQRS is a rhombus

Now,

In ΔABC, P and Q are the mid points of the sides B and AC respectively

PQ ∥ BC and PQ = 1/2 BC.             [By the midpoint theorem]

In ΔADC, Q and R are the mid points of the sides AC and DC respectively

By the mid-point theorem, we get,

QR ∥ AD  QR = 1/2 AD    [By the mid-point theorem]

$\therefore$QR = 1/2 BC              [AD = BC]

Now In ΔBCD,

RS∥BC and RS = 1/2 AD  [By the mid-point theorem]

RS= 1/2 BC    [AD = BC]

From above eqns.

PQ = QR = RS

$\therefore$ PQRS is a rhombus.

Hence proved

问题20.在等腰ΔABC中，基极AB会同时向P和Q方向生成，使得AP x BQ = AC2。证明ΔAPC〜ΔBCQ

解决方案：

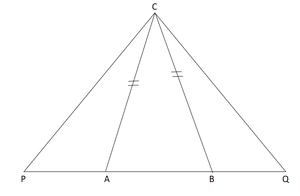
Given : ΔABC is isosceles ∆ and AP x BQ = AC²

To prove : ΔAPC∼ΔBCQ.

we know that, 

ΔABC is an isosceles triangle AC = BC.

AP x BQ = AC²  (given)

AP x BQ = AC x AC

AP x BQ = AC x BC

AP/BC = ABQ……….(1).

so, ∠CAB = ∠CBA    [as  AC = BC]

180° – ∠CAP = 180° – ∠CBQ [angles opposite to equal sides are EQUAL]

∠CAP = ∠CBQ ………..(2)

In ∆APC and ΔBCQ

AP/BC = AC/BQ [From equation 1]

∠CAP = ∠CBQ [From equation 2]

$\therefore$ΔAPC∼ΔBCQ  [By SAS similarity criterion]

Hence proved

问题21.一个身高90厘米的女孩以1.2 m / sec的速度从灯柱的底部走开。如果灯在离地面3.6m的高度，请在4秒钟后找到其阴影的长度。

解决方案：

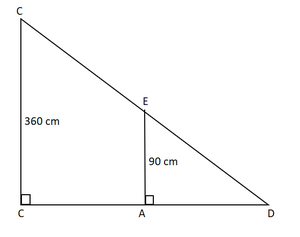
AD=1.2 m/sec ×4 sec =4.8 m =480 cm

Suppose the length of the shadow of the girl be x cm when she at position D. Therefore,

BD = x cm

In ∆BDE and ∆BAC,

∠BDE=∠BAC  [each90°]

∠DBE=∠ABC   [Common angle ]

$\therefore$ ∆BDE∼∆BAC   [ by AA similarity]

BE/BC=DE/AC=BD/AB  [Corresponding sides are proportional]

90/360=x/480+x

1/4= x/480+x

4x=480+x

4x−x=480

3x=480

x=480/3=160

Hence, the length of her shadow after 4 seconds is 160 cm.

问题22：一根长度为6 m的竖杆在地面上投射出一个长4m的阴影，同时，一个塔架则投射出一个长28m的阴影。找到塔的高度。

解决方案：

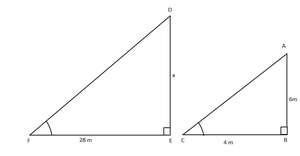
Let AB be stick and DE be tower.

A 6 m long stick casts a shadow of 4 m 

So,  AB = 6 m and BC = 4 m

Let DE casts shadow at the same time, So EF = 28 m

Let height of tower DE = x

Now in ∆ABC and ∆DEF,

∠B = ∠E (each 90°)

∠C = ∠F (shadows at the same time)

∆ABC ~ ∆DEF     [AA criterion]

AB/DE=BC/EF      [ Corresponding sides are proportional ]

$\therefore$6/x=4/28

x=42 m

Hence height of tower is 42 m

问题23。给定， ΔABC是C和DE C AB处的直角三角形。求证：ABCΔΔ〜ADE。因此找到AE和DE的长度。

解决方案：

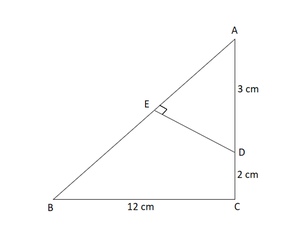
Given : ΔACB is right-angled triangle at C = 90°.

According to the figure : BC = 12 cm , AD=3 cm, DC = 2 cm.

AC = AD + DC = 3 +2= 5 cm

Now In ∆ACB,

AB² = AC² + BC² [by Pythagoras theorem]

AB² = 5² + 12²

AB² = 25 + 144 = 169

AB= √169 = 13  

$\therefore$AB = 13 cm

Now In  ΔABC & ΔADE,

∠BAC = ∠DAE     [common]

∠ACB = ∠AED      [each 90°]

$\therefore$ΔABC∼ΔADE     [by AA similarity criterion]

$\therefore$AB/AD = BC/DE = AC/AE    [ corresponding sides of two similar triangles are proportional]

13/3 = 12/ DE = 5/AE

13/3 = 12/DE

13 DE = 12×3  

DE = 36/13

13/3 = 5/AE

13 AE = 5×3

AE = 15/13

Hence, the length of DE= 36/13 & AE = 15/13

问题24.在图中，PA，QB和RC分别垂直于AC。证明1 / X + 1 / Z = 1 / Y

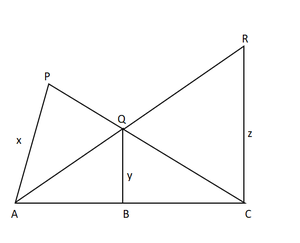
Given:

PA, QB and RC are each perpendicular to AC

To prove : 1/X+1/Z=1/Y

Now In ΔPAC and ΔQBC,

∠PCA = ∠QCB  [common angle]

∠PAC = ∠QBC [Coresponding angles]

$\therefore$ΔPAC ~ ΔQBC [by AA criteria]

$\therefore$PA/QB = AC/BC  [ Corresponding parts of similar triangles are proportional]

x/y = AB/BC  

y/x = BC/AC

Now In ΔRCA and ΔQBA,

∠RAC = ∠QAB [common angle]

∠RCA = ∠QBA [Coresponding angle]

$\therefore$ΔRCA ~ΔQBA  [by AA criteria]

$\therefore$RC/QB = AC/AB [ Corresponding parts of similar triangles are proportional]

z/y= AC/AB

y/z= AB/AC

y/z + y/z = BC + AC/ AC = 1  [by adding both eq we get]

y/z + y/z = 1

1/x + 1/z = 1/y [multiplying both sides by y]

Hence proved

问题25。给定，我们有AB∥CD∥EF。如果AB = 6厘米，CD = x厘米，EF = 10厘米，BD = 4厘米，DE = y厘米。计算x和y的值。

解决方案：

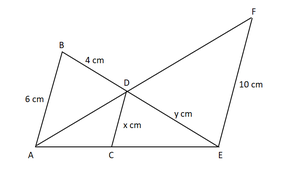
Given : AB || CD || EF , AB = 6 cm, CD = x cm, BD = 4 cm, and DE = y cm and EF = 10 cm.

Now In ∆ECD and ∆EAB,

∠CED = ∠AEB    [common]

∠ECD = ∠EAB   [corresponding angles]

$\therefore$∆ECD ~ ∆EAB ……….(1) [By AA similarity]

∴ EC/EA = CD/AB   [Corresponding parts of similar triangles are proportional]

EC / EA = x/6 ……………(2)

In ∆ACD and ∆AEF

∠CAD = ∠EAF [common]

∠ACD = ∠AEF [corresponding angles]

∆ACD ~ ∆AEF [By AA similarity]

∴ AC/AE = CD/EF     [Corresponding parts of similar triangles are proportional]

AC /AE = x/10 ……………..(3)

EC/EA+ AC /AE =  x/6 + x/10  [by Adding eq 2 & 3]

(EC + AC) /AE =( 5x + 3x)/30

AE / AE = 8x /30

1 = 8x/30

x = 30/8  

x = 3.75 cm

∆ECD ~ ∆EAB    [From eq  (i)]

DC/AB = ED /EB   [Corresponding parts of similar triangle are proportional]

3.75/6 = y/y+4

6y = 3.75(y+4)

6y = 3.75y + 15

6y – 3.75y = 15

2.25y = 15

y = 15/2.25

y = 6.67 cm

Hence, x = 3.75 cm and y = 6.67 cm.