第 10 类 RD Sharma 解决方案 - 第 4 章三角形 - 练习 4.6 |设置 2

问题 11. 两个相似三角形的面积分别为 121 cm ²和 64 cm ² 。如果第一个三角形的中值是 12.1 厘米，求另一个三角形的对应中值。

解决方案：

Let us consider ∆ABC and ∆DEF, AL and DM are the medians of ∆ABC and ∆DEF 

It is given that the area of ∆ABC = 121 cm² and area of ∆DEF = 64 cm²

AL = 12.1 cm

Let us assume DM = x cm

Given that, ∆ABC ~ ∆DEF

So, 

ar(∆ABC)/ar(∆DEF) = AL²/DM² 

= 121/64 = (12.1)²/x²

11/8 = 12.1/x 

⇒ x = (8 × 12.1)/11 = 8.8

Hence, the median of the second triangle is 8.8cm 

问题 12. 在 ΔABC ~ ΔDEF 中，AB = 5 cm 和 (ΔABC) = 20 cm ²和面积 (ΔDEF) = 45 cm ² ，确定 DE。

解决方案：

Given that,  

area (∆ABC) = 20 cm²

area (∆DEF) = 45 cm²

AB = 5 cm

Let us consider DE = x cm

Also, given that ∆ABC ~ ∆DEF

ar(∆ABC)/ar(∆DEF) = AB²/DE² 

⇒20/45 = (5)²/x²

⇒20/45 = 25/x² 

⇒x² = (25 × 45)/20 = 225/4 = (15/2)²

x = 15/2 = 7.5 

DE = 7.5cm

问题 13. 在 ΔABC 中，PQ 是一条线段，AB 在 P 处相交，AC 在 Q 处相交，使得 PQ || BC 和 PQ 将 ΔABC 分成面积相等的两部分。找到 BP/AB。

解决方案：

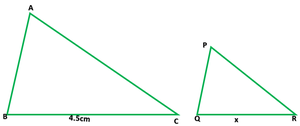
It is given that, in ∆ABC, PQ || BC and line PQ divide the ∆ABC into two parts 

∆APQ and trap. BPQC equally

i.e., area ∆APQ = area BPQC

Now we have to find BP/AB.

As we know that PQ||BC

So, ∆APQ ∼ ∆ABC

⇒ ar.(∆APQ)/ar.(∆ABC) = AP²/AB²

⇒ ar.(∆ABC)/ar.(∆APQ) = AB²/AP²

2/1 = AB²/AP²

{area ∆APQ = area trap. BPQC

 Area ∆ABC = 2area (∆APQ)}

⇒ AB/AP = √2/1 

⇒√2 AP = AB = AP + PB

⇒√2AP – AP = PB

⇒(√2 – 1)AP = PB

BP/AP = (√2 – 1)/1

问题 14. 两个相似三角形 ABC 和 PQR 的面积之比为 9 : 16。如果 BC = 4.5 cm，求 QR 的长度。

解决方案：

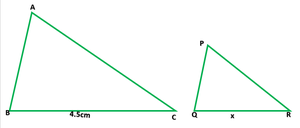
Given that, area (∆ABC) : area (∆PQR) = 9 : 16

∆ABC ~ ∆PQR

and BC = 4.5 cm

Let us considered QR = x cm

As we know that ∆ABC ~ ∆PQR

ar.(∆ABC)/ar.(∆PQR) = BC²/QR² ⇒ 9/16 = (4.5)²/x²

⇒ (3/4)² = (4.5/x)² ⇒ 4.5/x = 3/4

x = (4.5 × 4)/3 = 60

Hence, the length of QR is 6cm

问题 15. ABC 是一个三角形，PQ 是一条直线，在 P 中 AB 和 AC 在 Q 中。如果 AP = 1 cm，PB = 3 cm，AQ = 1.5 cm，QC = 4.5 cm，证明 ΔAPQ 的面积是ΔABC 面积的十六分之一。

解决方案：

Given that, in ∆ABC, P and Q are two points on line AB and AC 

AP = 1 cm, PB = 3 cm, AQ = 1.5 cm and QC = 4.5 cm

Now, AP/PB = 1/3 and AQ/QC = 1.5/4.5 = 1/3

In ∆APQ and ∆ABC

AP/PB = AQ/QC

PQ||BC

Hence, ∆APQ ∼ ∆ABC

So, ar.(∆APQ)/ar.(∆ABC) = AP²/PB² = AP²/(AP + PB)²

 ar.(∆APQ)/ar.(∆ABC) = 1²/(1 + 3)² = 1/16

Hence, area of ∆APQ = 1/16 of area of ∆ABC

问题 16. 如果 D 是 ΔABC 边 AB 上的一个点，使得 AD : DB = 3 : 2 并且 E 是 BC 上的一个点，使得 DE ||交流。求 ΔABC 和 ΔBDE 的面积比。

解决方案：

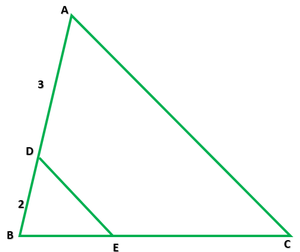
Given that in ∆ABC, D is a point on AB such that AD : DB = 3 : 2

DE||AC

In ∆BDE and ∆ABC

∠BDE = ∠A

∠DBE = ∠ABC

So, by AA, ∆BED ∼ ∆ABC

Therefore, ar.(∆ABC)/ar.(∆BDE) = AB²/BD² = (BD + AD)²/BD²

= (2 + 3)²/2² = 5²/2² = 25/4

Hence, the ratio of areas of ∆ABC and ∆BDE is 25:4

问题 17. 如果 ΔABC 和 ΔBDE 是等边三角形，其中 D 是 BC 的中点，求 ΔABC 和 ΔBDE 的面积比。

解决方案：

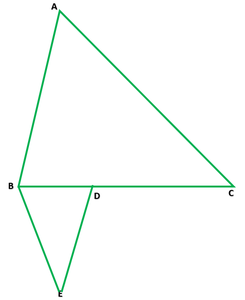
Given that ∆ABC and ∆DBE are equilateral triangles, where D is mid point of BC

So, BD = 1/2BC

Now area of ∆ABC

√3/4(side)² = √3/4BC²

and area of ∆DBE

√3/4(side)² = √3/4BD²

√3/4(side)² = √3/4(1/2BC)²

√3/4(side)² = √3/16(BC)²

So, the ratio between areas is

= area(∆ABC)/area(∆DBE) =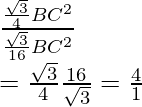$\frac{\frac{\sqrt{3}}{4}BC^2}{\frac{\sqrt{3}}{16}BC^2}\\ =\frac{\sqrt{3}}{4}×\frac{16}{\sqrt{3}}=\frac{4}{1}$

Hence, the ratio of areas of ∆ABC and ∆BDE is 4:1

问题 18. 两个等腰三角形的垂直角相等，面积之比为 36 : 25。求它们对应的高度之比。

解决方案：

Let us consider two triangles, ∆ABC and ∆XYZ and these triangles have equal vertical angle, i.e., ∠A and ∠X

And AD and XO is the heights of these triangles.

So, ∆ABC/∆XYZ = AB/AC = XY/XZ

In ∆ABC and ∆XYZ 

∠A = ∠X

AB/AC = XY/XZ

So, by SAS

∆ABC ~ ∆XYZ

So, ar(∆ABC)/ar(∆XYZ) = AD²/XO²

As we know that ar(∆ABC)/ar(∆XYZ) = 36/25

So, 

36/25 = AD²/XO²

6/5 = AD/XO

Hence, the ratio of their corresponding heights is 6:5

问题 19. 图中，ΔABC 和 ΔDBC 在同一个基数 BC 上。如果 AD 和 BC 在 O 处相交，证明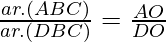$\frac{ar.(∆ABC)}{ar.(∆DBC)}=\frac{AO}{DO}$

解决方案：

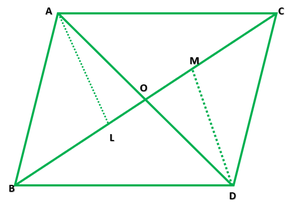
Given that two ∆ABC and ∆DBC are on the same base BC as shown in the given figure

AC and BD intersect each other at O

Now, Draw AL ⊥ BC and DM ⊥BC

Prove: $\frac{ar.(∆ABC)}{ar.(∆DBC)}=\frac{AO}{DO}$

Proof: 

In ∆ALO and ∆DMO,

∠L =∠M = 90°

∠AOL = ∠DOM [Vertically opposite angles]

So, by AA, ∆ALO ∼ ∆DMO       

So, AL/DM = AO/DO 

Now 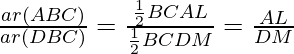$\frac{ar(∆ABC)}{ar(∆DBC)}=\frac{\frac{1}{2}BC×AL}{\frac{1}{2}BC×DM}=\frac{AL}{DM}$

But AL/DM = AO/DO      (Proved above)

So, $\frac{ar.(∆ABC)}{ar.(∆DBC)}=\frac{AO}{DO}$ 

Hence proved

问题 20. ABCD 是一个梯形，其中 AB ||光盘。对角线 AC 和 BD 相交于 O。证明

(i) ΔAOB ~ ΔCOD

(ii) 如果 OA = 6 cm，OC = 8 cm，求

(a)ar(ΔAOB)/ar(ΔCOD) (b) ar(ΔAOD)/ar(ΔCOD)

解决方案：

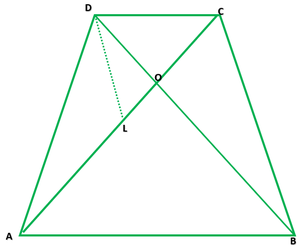
Given that ABCD is a trapezium in which AB || CD and the diagonals AC and BD intersect at O

Now, in the figure from point D, draw DL⊥AC

(i) In ∆AOB and ∆COD

∠AOB =∠COD            [Vertically opposite angles]

∠OAB =∠OCD           [Alternate angles]

So, by AA criterion

∆AOB ~ ∆COD         

(ii) Given that OA = 6 cm, OC = 8 cm

As we know that ∆AOB ~ ∆COD     

So, OA/OC = OB/OD = AB/CD

(a) ar(∆AOB)/ar(∆COD) = AO²/OC²

= 6²/8² = 36/64 = 9/16 

Therefore, ar(∆AOB)/ar(∆COD) = 9/16 

(b) As we know that ∆AOD and ∆COD have their bases on the same line and their vertex A is common

Therefore,  ar(∆AOD)/ar(∆COD) = AO/OC = 6/8 = 3/4   

问题 21. 在 ΔABC 中，P 将边 AB 相除，使得 AP : PB = 1 : 2。Q 是 AC 中的一个点，使得 PQ ||公元前。求 ΔAPQ 和梯形 BPQC 的面积比。

解决方案：

Given that, ABC is a triangle, in which P divides the side AB such that 

AP : PB = 1 : 2. Q is a point in AC such that PQ || BC

In ∆APQ and ∆ABC

∠APQ = ∠B

∠PAQ = ∠BAC

So, by AA criterion

∆APQ ∼ ∆ABC

So, 

ar(∆APQ)/ar(∆ABC) = (AP)²/(AB)²

ar(∆APQ)/ar(∆ABC) = (1)²/(1 + 2)² = (1)²/(3)² = 1/9

9 ar(∆APQ) = ar(∆ABC)

9 ar(∆APQ) = ar(∆APQ) + ar(trap. BPQC)

9 ar(∆APQ) = ar(trap BPQC)

ar(∆APQ)/ar(trap BPQC) = 1/9

Hence, the ratio of the areas of ∆APQ and trapezium BPQC is 1:9

问题 22. AD 是等边三角形 ABC 的高。以AD为底，构造另一个等边三角形ADE。证明面积 (ΔADE) : 面积 (ΔABC) = 3 : 4。

解决方案：

Given that AD is an altitude of an equilateral triangle ABC. 

On AD as base, another equilateral triangle ADE is constructed

Prove: Area (∆ADE) : Area (∆ABC) = 3 : 4

Proof:

Area of ∆ABC = √3/4 BC²

and AD = √3/2 BC 

Area of ∆ADE = √3/4 AD²

= √3/4 (√3/2 BC)² = 3√3/16 BC²

So, the ratio of area (∆ADE):area(∆ABC) = 3√3/16 BC² : √3/4 BC²

= 3/4:1 = 3:4