第11类RD Sharma解-第22章直角坐标直角坐标系的简要说明-练习22.1

问题1.如果连接点P(x ₁ ，y ₁ )和Q(x ₂ ，y ₂ )的线段在原点O处对角,，则证明OP.OQcos∅= x ₁ x ₂ + y ₁ y ₂ 。

解决方案：

Since, O is the origin, we can get, OP² = x₁² + y₁²  and OQ² = x₂² + y₂²

Also, by the distance formula we know distance between two points P and Q is:

PQ² = (x₂ – x₁)² + (y₂ – y₁)²

Using the cosine formula, in triangle OPQ, we have

PQ² = OP² + OQ² – 2 (OP). (OQ) cos∅

⇒  (x₂ – x₁)² + (y₂ – y₁)² =  x₁² + y₁² +  x₂² + y₂²  – 2 (OP). (OQ) cos∅

⇒ x₂² + x₁² – 2 x₂x₁ + y₂² + y₁² – 2y₂y₁ = x₁² + y₁² +  x₂² + y₂²  – 2 (OP). (OQ) cos∅

⇒ – 2 (x₁x₂ + y₁y₂) =  – 2 (OP). (OQ) cos∅

⇒ OP.OQ cos∅ = x₁x₂ + y₁y₂

问题2.三角形ABC的顶点是A(0,0)，B(2，-1)和C(9,0)。查找cosB。

解决方案：

Using the cosine formula, we know

$cos B = \frac{a^2 + c^2 - b^2}{2ac}$

Now, lets assume, a = BC, b = CA and c = AB are the sides of the triangle ABC.

Therefore, the distance between two consecutive points can be calculated as:

a = BC = $\sqrt{(9-2)^2 + (2+1)^2} = \sqrt{49 + 9} = \sqrt{58}$

b = CA = $\sqrt{(0-9)^2 + (0+2)^2} = \sqrt{81 + 4} = \sqrt{85}$

and c = AB = $\sqrt{(2-0)^2 + (-1 - 0)^2} = \sqrt{4 + 1} = \sqrt{5}$

Using the cosine formula,

$cos B = \frac{58 + 5 - 85}{2\times\sqrt{58}\times \sqrt{5}}$

$= \frac{63 - 85}{2\times\sqrt{290}}$

$= \frac{-22}{\sqrt{290}} = \frac{- 11}{\sqrt{290}}$

Hence, $cosB = \frac{- 11}{\sqrt{290}}$

问题。 3四个点A(6,3)，B(-3,5)，C(4，-2)和D(x，3x)的给出方式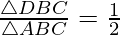$\frac{\triangle DBC}{\triangle ABC} = \frac{1}{2}$ ，找到x。

解决方案：

We know the formula that,

area of a triangle = $\frac{1}{2}[x_1(y_2-y_1) + x_2(y_3-y_2) + x_3(y_3-y_1)]$, so

area of triangle ABC = $\frac{1}{2}[-3(-2-3x) + 4(3x-5) + x(5+2)]$

= $\frac{1}{2}[6+ 9x+ 12x -20 + 5x +2x]$

= $\frac{1}{2}[28x -14] = 14x - 7$

Similarly, area of triangle DBC = $\frac{1}{2}[6(5+2) - 3(-2-3) + 4(3-5)]$

= $\frac{1}{2}[42+15-8]$

= $\frac{49}{2}$

Now, we are given that

$\frac{\triangle DBC}{\triangle ABC} = \frac{1}{2}$

$\Rightarrow \frac{7(2x-1)}{\frac{49}{2}} = \frac{1}{2}$

$\Rightarrow \frac{14(2x-1)}{49} = \frac{1}{2}$

$\Rightarrow \frac{28x-14}{49} = \frac{1}{2}$

$\Rightarrow 56x - 28 = 49$

$\Rightarrow 56x = 77 \\\Rightarrow x = \frac{11}{8}$

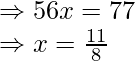
问题。 4点A(2,0)，B(9,1)，C(11,6)和D(4,4)是四边形ABCD的顶点。确定ABCD是否为菱形。

解决方案：

We know the property of a rhombus that the diagonals bisect each other at the right angles. Thus, both the diagonals must have a common mid-point.

Now mid-point of line AC = $\left ( \frac{2 + 11}{2} \right ), \left ( \frac{0 + 6}{2} \right )$ = (13/2, 3)

and mid-point of line BD = $\left ( \frac{9 + 4}{2} \right ), \left ( \frac{1 + 4}{2} \right )$ = $\left ( \frac{13}{2}, \frac{5}{2} \right )$

Since, both the lines have different mid-points, we can conclude that the quadrilateral ABCD is not a rhombus.

问题5。找到刻在顶点为(-36,7)，(20,7)和(0，-8)的三角形中的圆心的坐标。

解决方案：

Since, the circle is inscribed in a triangle, the centre of the circle is known as incentre. We know that incentre of a circle (O) inscribed in a triangle is given by the formula:

O = $\left ( \frac{ax_1 + bx_2 + cx_3}{a+b+c},\frac{ay_1 + by_2 + cy_3}{a+b+c} \right )$, where a, b, c  are length opposite to ∠A, ∠B and ∠C respectively.

Therefore, lets say a = BC = $\sqrt{(20-0)^2 + (7-(-8))^2} = \sqrt{20^2 + 15^2} = 25$

similarly, b = AC = $\sqrt{(-36-0)^2 + (7-(-8))^2} = \sqrt{36^2 + 15^2} = \sqrt{1521} = 39$

and c = AB = $\sqrt{(-36-20)^2 + (7-7)^2} = 56$

Therefore, the coordinates of the incentre will be:

O = $\left (\frac{25(-36)+39(20)+56(0)}{25+39+56},\frac{25(7)+39(7)+56(-8)}{25+39+56}\right )$

$= \left (\frac{-1}{120},0\right )$

 = (-1,0)

Hence, the coordinate of the centre of the circle is (-1,0)

问题6：等边三角形(边2a)的底边沿y轴放置，以使底边的中点位于原点。找到三角形的顶点。

解决方案：

Since, ABC is an equilateral triangle it will have each sides equal, i.e, AB = BC = CA = 2a

Also, area of an equilateral triangle  = $\frac{\sqrt{3}}{4} \times a^2$ , where a is the side of the triangle.

Therefore, area of given triangle = $\frac{\sqrt{3}}{4} \times (2a)^2 = \sqrt{3}a^2$

Also, area of a triangle = $\frac{1}{2}\times base \times height$

$\Rightarrow \sqrt{3}a^2 = \frac{1}{2}\times BC \times OA$

$\Rightarrow \sqrt{3}a^2 = \frac{1}{2}\times 2a \times OA$

$\Rightarrow \sqrt{3}a = OA$

Thus, the coordinates of point A is $\left (\sqrt{3}a,0 \right )$

similarly, the coordinates of point B is (0,-a) and the coordinates of point C is (0,a)

Hence, the vertices of a triangle are (0,a), (0,-a) and  $\left (-\sqrt{3}a,0 \right )$ or (0,a), (0.-a) and $\left (\sqrt{3}a,0 \right )$

问题7.当(i)PQ平行于y轴，(ii)PQ平行于x轴时，求出P(x1，y1)与Q(x2，y2)之间的距离。

解决方案：

We are given two points P(x1,y1) and Q(x2,y2),

(i) when line  PQ is parallel to the y-axis, then we can conclude that the x-coordinate will be constant ⇒ x2 = x1

Thus, by using distance formula:

PQ = $\sqrt{(x2-x1)^2 + (y2-y1)^2} = \sqrt{(0)^2 + (y2-y1)^2} = |y2-y1|$

(ii) when line  PQ is parallel to the x-axis, then we can conclude that the y-coordinate will be constant ⇒ y2 = y1

Thus, by using distance formula:

PQ = $\sqrt{(x2-x1)^2 + (y2-y1)^2} = \sqrt{(x2-x1)^2 + (0)^2} = |x2-x1|$ 

问题8.在x轴上找到一个与点(7,6)和(3,4)等距的点。

解决方案：

As given in the question, let the arbitrary point C that lies on the x-axis has coordinate (x,0). Now, this point is equidistant from both the coordinates (7,6) and (3,4), therefore by using distance formula, we get

$\sqrt{(x-7)^2 + (0-6)^2} = \sqrt{(x-3)^2 + (0-4)^2}$

$\Rightarrow (x-7)^2 + (6)^2 = (x-3)^2 + (4)^2$

$\Rightarrow x^2 -14x + 49 + 36 = x^2 -6x + 9 + 16$

$\Rightarrow 8x = 60 \Rightarrow x = \frac{15}{2}$

Therefore, coordinate of the point on the x-axis is $(\frac{15}{2},0)$