问题1.“失败”一词的字母可以以几种方式排列,以使辅音仅占据奇数位置?
解决方案:
From the given word, we get
F, L, R = 3 consonants
A, I, U, E = 4 vowels
1, 3, 5, 7 = 4 odd positions possible
Out of these 4 positions select 3 positions for the 3 given consonants = 4P3 = 4 ways
Now for these positions, ways to arrange consonants = 3! = 6
And ways to arrange the vowels in remaining positions are = 4! = 24
Total ways = 4 x 6 x 24 = 576
问题2:“ STRANGE”一词的字母可以以几种方式排列,以便
(i)元音在一起吗?
(ii)元音永远不会在一起吗?和
(iii)元音仅占据奇数位?
解决方案:
(i) 2 vowels are given, for these to be together let the first of two vowels occupy a position p
Now, there are 6 ways in which p can be chosen.
(All 7 positions except the last position, because if the first vowel
comes at the last position, no position will be left there for the second vowel)
For each p chosen, the vowels can be put in two orders (AE, EA) = 2 ways
Remaining letters can be arranged in = 5! = 120 ways
Total ways = Ways of choosing positions for vowels x
Ways to arrange the vowels x
Ways to arrange the remaining letters
= 6 x 2 x 120 = 1440
(ii) Let the first vowel be at position p.
p can be chosen in 6 different ways (1 to 6).
When first vowel is at p, then second can be from p+2 to 7 so that not consecutive.
= 7 – (p + 2) + 1 = (6 – p)ways
Case 1 : p = 1 ⇒ 6 – p = 5
Case 2: p=2 ⇒ 6 – p = 4
and so on till 6 – p = 0 for Case 6.
No. of ways of selecting vowels positions in the word = 5 + 4 + 3 + 2 + 1 + 0 = 15
For each selection, ways to put the vowels = 2 (AE and EA)
Ways of putting the remaining letters = 5! = 120
Total ways = 15 x 2 x 120 = 3600
(iii) Choosing 2 odd positions from 4 = 4P2 = 4 x 3 / 2 = 6
Ways of arranging two vowels in selected positions = 2! = 2
Ways of arranging other letters are = 5! = 120
Total ways = 6 x 2 x 120 = 1440
问题3.“ SUNDAY”一词的字母可以形成多少个词?其中有多少以D开头?
解决方案:
Total number of letters present in the given word = 6
So, ways to arrange 6 letters to get the words = 6! = 720
Now, when D is fixed at position 1, remaining 5 can be arranged in ways = 5! = 120
问题4.“东方”一词的字母中可以形成多少个词,以使元音始终占据奇数?
解决方案:
From the given word, we get 4 vowels and 4 odd positions possible (1, 3, 5, 7)
So, the ways to arrange the vowels = 4! = 24
Ways to arrange consonant letters = 4! = 24
Total ways = 24 x 24 = 576
问题5.“ SUNDAY”一词的字母可以形成多少个不同的词?多少个单词以N开头?有多少以N开头并以Y结尾?
解决方案:
Total number of letters present in the given word = 6
Now, Ways to arrange the 6 letters to get the words = 6! = 720
So now we find how many words begin with N
Let the fix N on the first position and remaining letter is 5
So the arrangement of 5 letters can be in 5! ways = 120 ways
Now find how many begin with N and end in Y
Let fix Y at position number 6 and N at position number 1 and the remaining letter is 4
So, the arrangement of 4 letters can be in 4! ways = 24 ways
问题6.“ GANESHPURI”一词的字母可以形成多少个不同的词?用多少个这样的词:
(i)字母G始终排在第一位吗?
(ii)字母P和I分别占据首位和最后一位?
(iii)元音是否总是在一起?
(iv)元音总是占据偶数位置吗?
解决方案:
Given: Total number of letters present in the given word = 10
(i) Fix G at position number 1 and the remaining letters are 9
So, the remaining letters can be arranged 9! = 51840 ways
(ii) The letter P and I respectively occupy the first and last place and the remaining letters are 8
So, the remaining letters can be arranged 8! = 5760 ways
(iii) Total number of vowels present = 4
The first vowel can be at max at position 7 (otherwise remaining vowels would
not have enough required positions)
So from 1 to 7 positions first vowel can be put at 7P1 = 7 ways
Remaining will be put in next consecutive positions in the word. (so 1 way)
Ways to select the vowels positions = Ways to put first vowel x Ways to put remaining vowels
= 7 x 1 = 7 ways
Ways to arrange the 4 vowels in these 4 selected positions = 4! = 24 ways
Ways to arrange the consonant letters will be = 6! = 720 ways
Total words having vowels always together = Ways to choose the vowels positions x
Ways to arrange vowels x
Ways to arrange consonants
= 7 x 24 x 720
= 120960
(iv) 5 positions possible that are even (2, 4, 6, 8, 10)
We have 4 vowels and need to choose 4 even positions = 5P4 = 5 ways
Ways to arrange these 4 vowels = 4! = 24
Ways to arrange the 6 consonants = 6! = 720
Total words = 5 x 24 x 720
= 86400
问题7:“ VOWELS”一词的字母可以形成多少个排列
(i)信件没有限制吗?
(ii)每个词都以E开头?
(iii)每个词都以O开头,以L结尾?
(iv)所有的元音都聚集在一起吗?
(v)所有辅音一起出现吗?
解决方案:
Given: Total number of letters = 6
(i) Ways to arrange 6 letters are = 6! = 720
(ii) Fix E at first position and the remaining letters are 5
So, the remaining letters can be arranged = 5! = 120 ways
(iii) Fix O at 1st and L at last position. So the remaining 4 letters
These 4 letters can be arranged = 4! = 24 ways
(iv) 2 vowels together can consider them 1 symbol = 2 ways for this new symbol (EO and OE)
1 symbol and 4 letters = 5 things are to be arranged so number of ways = 5! =120
Total ways = 120 x 2 = 240
(v) Consonants together = VWLS are 1 group = 4! ways
Group of consonants and 2 vowels = 3 things = 3! ways to arrange
Total ways = 4! x 3! = 144
问题8.“ ARTICLE”一词的字母中可以形成多少个词,从而使元音占据偶数位置?
解决方案:
In the given word, we have 3 vowels and also 3 even positions there
So 3! ways to occupy places for vowels.
For consonants = 4! = 24 ways
Total words = 3! x 4! = 144
问题9.如果没有夫妻在同一场地比赛,可以由七对已婚夫妇以多种方式构成草坪网球混双?
解决方案:
2 teams with 1 man and 1 woman
Need to select 2 man so number of ways are = 7P2 = 21
Need to select 2 woman out of 5 (except wives of selected men), ways = 5 P2 = 10
Now, ways to assign teams to men are = 2 (1st man to team A or to team B)
Similarly, for women too = 2 ways
Number of required ways = 21 x 10 x 2 x 2 = 840
问题10:男人和女人要排成一排,这样就不会有两个女人坐在一起。如果m> n则表明它们可以就座的方式为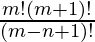
解决方案:
Let us first seat the men = m! ways
Now, m+1 spaces are created for women tor sit.
(before 1st man, between two consecutive men, after last seated man)
Out of these m+1 spaces, we need to choose n spaces for the women = m+1Pn possible ways
Arrange women in n! ways after selecting seats for them above.
Total ways to seat = m! x n! x (m+1)! / ( (m + 1 – n!) x n! )
= m! (m+1)! / (m+1-n)!
Hence, shown.
问题11.假设没有重复字母,则从单词MONDAY中的字母可以组成多少个单词(带或不带字典含义),如果
(i)一次使用4个字母?
(ii)一次使用所有字母?
(iii)使用所有字母,但首先是元音?
解决方案:
(i) Select 4 letters out of 6 = 6P4 = 6 x 5 / 2 = 15
Ways to arrange these = 4! = 24
Total such words possible = 15 x 24 = 360
(ii) Number of such words = 6! = 720
(iii) Possibilities for first position = 2 (O or A)
Number of arrangements for other positions in the word are = 5!
Total words = 2 x 5! = 240
问题12.使用“东方”一词可以制作多少个三个字母的单词?
解决方案:
Total number of the letters present in the given word = 4
Select 3 letters out of 8 = 8P3 = 56 ways
We have 3! ways to arrange
Hence, the total words = 56 x 3! = 336