第9类RD Sharma解决方案–第16章圈子-练习16.2

问题1.圆的半径为8厘米，其中一个弦的长度为12厘米。找出和弦与中心的距离。

解决方案：

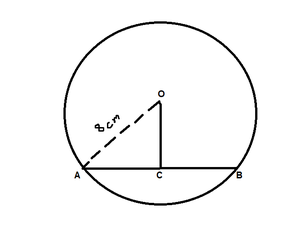
According to the question, given that 

Radius(OA) = 8 cm 

Chord (AB) = 12cm

Find: the distance of the chord from the centre, i.e., OC

So, draw a perpendicular OC on AB.

As we know that, perpendicular from centre to chord bisects the chord

So, AC = BC = 12/2 = 6 cm

Now in ΔOCA,

By using Pythagoras theorem,

OA² = AC² + OC²

64 = 36 + OC²

OC² = 64 – 36 = 28

OC = √28 

OC = 5.291 (approx.)

Hence, the distance of the chord from the centre is 5.291 cm.

问题2。找到与半径为10 cm的圆的中心相距5 cm的和弦的长度。

解决方案：

According to the question, given that 

Distance of the chord from the centre(OC) = 5 cm

Radius(OA) = 10 cm 

Find: the length of a chord AB

So, In ΔOCA,

By using Pythagoras theorem,

OA² = AC² + OC²

100 = AC² + 25

AC² = 100 – 25 = 75

AC = √75 = 8.66

As we know that, perpendicular from centre to chord bisects the chord

So, AC = BC = 8.66 cm

=> AB = AC + BC = 8.66 + 8.66 = 17.32

Hence, the length of chord AB is 17.32 cm

问题3：找到和半径为6 cm的圆的中心相距4 cm的弦的长度。

解决方案：

According to the question, given that 

Distance of the chord from the centre(OC) = 4 cm

Radius (OA) = 6 cm 

Find: the length of a chord, i.e., AB

So, in ΔOCA,

By using Pythagoras theorem,

OA² = AC² + OC²

36 = AC² + 16

AC² = 36 – 16 = 20

AC = √20 = 4.47

AC = 4.47cm

As we know that, perpendicular from centre to chord bisects the chord

So, AC = BC = 4.47 cm

=> AB = AC + BC = 4.47 + 4.47 = 8.94

Hence, the length of chord AB is 8.94 cm

问题4.分别长为5 cm，11 cm的两个和弦AB，CD平行。如果AB与CD之间的距离为3厘米，请找到圆的半径。

解决方案：

According to the question, given that 

The length of chord AB = 5 cm

The length of chord CD = 11 cm

PQ = 3 cm

Find: the radius of the circle, i.e., r

So, draw perpendiculars OP on CD and OQ on AB

Let us assume OP = x cm and OC = OA = r cm

As we know that, perpendicular from centre to chord bisects the chord

OP⊥CD, 

So, CP = PD = 11/2 cm

And OQ⊥AB

So, AQ = BQ = 5/2 cm

Now, in ΔOCP,

By using Pythagoras theorem,

OC² = OP² + CP²

r² = x² + (11/2) ² …..(1)

In ΔOQA,

By using Pythagoras theorem,

OA² = OQ² + AQ²

r² = (x + 3)² + (5/2)² …..(2)

From equations (1) and (2), we get

(x + 3)² + (5/2)² = x² + (11/2)²

x² + 6x + 9 + 25/4 = x² + 121/4

By using identity, (a + b)² = a² + b² + 2ab 

6x = 121/4 – 25/4 − 9

6x = 15

or x = 15/6 = 5/2

Now, substitute the value of x in equation (1), we get

r² = (5/2)² + (11/2) ²

r² = 25/4 + 121/4

r² = 146/4

r = √146/4 cm

Hence, the radius of the circle is √146/4 cm

问题5.给出找到给定圆心的方法。

解决方案：

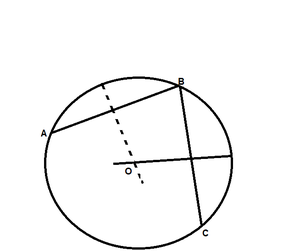
Steps of Construction:

Step 1: Let us assume three points, i.e., A, B and C on a circle.

Step 2: Join AB and BC.

Step 3: Now draw perpendicular bisectors of chord AB and BC that intersect each other at a point O.

Step 4: As we know that the perpendicular bisectors of chord always pass through the centre, so the centre of the circle is point O.

问题6.证明将弦的中点连接到圆心的线穿过相应的小弧的中点。

解决方案：

According to the question, 

Prove: D is the mid-point of arc AB.

Proof:

From the given figure, 

Let us assume C is the mid-point of chord AB.

Now, In ΔOAC and ΔOBC

OA = OB [Radius of circle]

OC = OC [Common]

AC = BC [C is the mid-point of chord AB]

By SSS condition

ΔOAC ≅ ΔOBC

Hence, BY C.P.C.T

∠AOC = ∠BOC

m(AD) ≅ m(BD)

AD ≅ BD

Hence Proved.

问题7：证明将圆的弦二等分的圆的直径也将圆的中心对弦所成的角度二等分。

解决方案：

According to the question, 

Prove: PQ bisects ∠AOB

Proof:

Form the given figure, we get 

PQ is a diameter of circle which bisects the chord AB at C. 

In ΔBOC and ΔAOC

OA = OB [Radius]

OC = OC [Common side]

AC = BC [Given]

By SSS condition

ΔAOC ≅ ΔBOC

Hence, BY C.P.C.T

∠AOC = ∠BOC 

So, PQ bisects ∠AOB

Hence proved.

问题8.证明两个不同的圆不能相交超过两个点。

解决方案：

Prove: two different circles cannot intersect each other at more than two points.

Proof:

Let us considered the two circles intersect in three points, i.e., A, B and C.

Now as we know that, points A, B, and C are non-collinear. 

So, a unique circle passes through these three points(i.e., A, B, C).

Now, this is a contradiction to the fact that the two given circles are passing through A, B, C.

Hence, two circles cannot intersect each other at more than two points.

Hence, proved.

问题9.线段AB的长度为5厘米。画一个穿过A和B的半径为4厘米的圆。您能画一个穿过A和B的半径为2厘米的圆吗?给出理由以支持您的答案。

解决方案：

According to the question, given that

A line segment AB = 5 cm, 

One circle having radius r1 = 4 cm which is passing through point A and B 

and other circle having radius r2 = 2 cm.

As we know that the largest chord of any circle is equal to the diameter of that circle. 

So, 2 × r2 < AB 

Hence, there is no possibility to draw a circle whose diameter is smaller than the length of the chord.  

问题10：边长为9 cm的等边三角形切成一个圆。找到圆的半径。

解决方案：

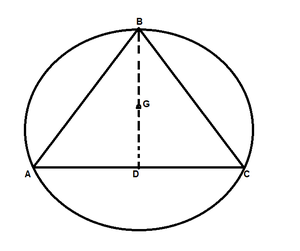
According to the question,

Let us considered ABD is the equilateral triangle and the side of the triangle is 9cm

and AD is one of its median.

Find: the radius of the circle

So, 

Let us assume G be centroid of ΔABC 

Then AG:GD = 2:1

As we know that in an equilateral triangle, the centroid coincides with circumcentre,

So, G is centre of circumference with circumradius GA.

Also, G is the centre and GD ⊥ BC, 

So, in ΔADB

AB² = AD² + DB²

9 = AD² + (9/2)²

AD = 9√3/2 cm

Now we find the radius(AG) of the circle 

AG = (2/3) × AD

= 3√3 cm

Hence, the radius of the circle is 3√3 cm

问题11.给定圆弧，完成圆。

解决方案：

Steps of Construction:

Step 1: Let us considered three points i.e., A, B and C on the given arc

Step 2: Join AB and BC

Step 3: Now draw the perpendicular bisectors of chords AB and BC which intersect each other at point O.

So, the centre of the circle is O. 

Step 4: Now join OA

Step 5: Hence, the centre of the circle is O, so the radius of the circle is OA.

Hence, the complete the circle.

问题12.绘制不同的圆对。每对有多少个共同点?共同点的最大数量是多少?

解决方案：

Here, the first set of circles contains 2 common points, Second set of circles contains 1 common points, and

third set of circles contains 0 common points.

Hence, the maximum number of common points are 2.

问题13.假设您有一个圆圈。进行施工以找到其中心。

解决方案：

Steps Of Construction:

Step 1: Let us considered three points i.e., A, B and C on the given circle.

Step 2: Join AB And BC.

Step 3: Now draw the perpendicular bisectors of chord AB and BC which intersect each other at point O.

Step 4: As we know that the perpendicular bisectors of chord always pass through the centre, so the centre of the circle is point O.

问题14：两个和弦AB和CD的长度分别为一个圆的5厘米和11厘米，彼此平行，并且位于其中心的相对侧。如果AB与CD之间的距离为6厘米，请找到圆的半径。

解决方案：

According to the question, given that

The length of chod AB = 5cm

The length of chod CD = 11cm

The distance between AB and CD(i.e., MN) = 6cm

Find: the radius of the circle

So, draw OM ⊥ AB and ON ⊥ CD

Now, join OB and OD

As we know that, perpendicular from centre to chord bisects the chord

So, BM = AB/2 = 5/2

ND = CD/2 = 11/2

Let us assume ON be x, so OM will be 6 – x.

In ΔMOB,

OM² + MB² = OB²

(6 – x)² + (5/2)² = OB²

36 + x² – 12x + 25/4 = OB²  ………(i)

In ΔNOD,

ON² + ND² = OD²

x² + (11/2)² = OD²

x² + 121/4 = OD²  ………(ii)

We have OB = OD (radii of same circle)

So from eq(i) and (ii), we get

36 + x² – 12x +25/4 = x² +121/4

12x = 36 + 25/4 – 121/4

12x = 48/4

x = 1

Now put the value of x in eq(i), we get 

OD² = 1 + 121/4

OD = 5√5/2 

Hence, the radius of circle is 5√5/2 

问题15：一个圆的两个平行弦的长度分别为6cm和8cm。如果较小的和弦与中心的距离为4cm，则另一个和弦与中心的距离为多少?

解决方案：

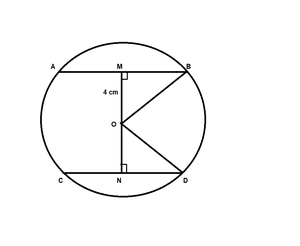
According to the question, given that

The length of chod AB = 6cm

The length of chod CD = 8cm

The distance between the chord AB and the centre(OM) = 4 cm

Find: The distance between the chord CD and the centre(ON)

So, MB = AB/2 = 6/2 = 3cm

In ΔOMB,

OM² + MB² = OB²

4² + 9² = OB²

OB = 5cm

In ΔOND,

OD = OB = 5cm [radii of same circle]

ND = CD/2 = 8/2 = 4cm

ON² + ND² = OD²

ON² + 4² = 5²

ON² = 25 – 16

ON = 3cm

Hence, The distance between the chord CD and the centre(ON) is 3cm.