11类RD Sharma解决方案–第30章导数–练习30.2 |套装2

问题3.使用第一原则区分以下每个方面：

(i)xsinx

解决方案：

Given that f(x) = xsinx

By using the formula

$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

We get

= $\lim_{h\to 0}\frac{(x+h)sin(x+h)-xsinx}{h}$

= $\lim_{h\to 0}\frac{x(sin(x+h)-sinx)}{h}+sin(x+h)$            

Using the formula 

sinc – sind = 2cos((c + d)/2)sin((c – d)/2)

We get

= $\lim_{h\to 0}\frac{x×2cos(x+h/2)sin(h/2)}{h}+sin(x+h)$       

As we know that $\lim_{θ\to 0}\frac{sinθ}{θ}=1$

So, 

= 2x × cosx × 1/2 + sinx

= x × cosx + sinx

= sinx + xcosx

(ii)xcosx

解决方案：

Given that f(x) = xcosx

By using the formula

$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$ 

We get

= $\lim_{h\to 0}\frac{(x+h)cos(x+h)-xcosx}{h}$

= $\lim_{h\to 0}\frac{xcos(x+h)hcos(x+h)-xcosx}{h}$

= $\lim_{h\to 0}\frac{x(cos(x+h)-cosx)}{h}+cos(x+h)$

= $\lim_{h\to 0}x.2sin(x-x+h/2)sin(x+h/2)+cos(x+h) [cosA-cosB=2sin(\frac{B-A}{2})sin(\frac{B+A}{2})]$

= $\lim_{h\to 0}\frac{2x.sin(-h/2)sin(x+h/2)}{h}+cos(x+h)$

= -xsinx + cosx

(iii)罪(2x – 3)

解决方案：

Given that f(x) = sin(2x – 3)

By using the formula

$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

We get

= $\lim_{h\to 0}\frac{sin[2(x+h)-3]-sin(2x-3)}{h}$

= $\lim_{h\to 0}\frac{2cos\frac{(2x+2h-3+2x-3)}{2}×sin\frac{(2x+2h-3-2-x+3)}{2}}{h}$

Using the formula

sinC – sinD = 2cos{C+D}/2sin{C-D}/2

= $\lim_{h\to 0}2cos(2x-3+h).\frac{sinh}{h}$           

As we know that, \lim_{θ\to 0}\frac{sinθ}{θ}=1 so,

= 2cos(2x – 3)

(iv)√sin2x

解决方案：

Given that f(x) = √sin2x

By using the formula

 $f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

We get

= $\lim_{h\to 0}\frac{\sqrt{sin2(x+h)}-\sqrt{sin2x}}{h}$

On multiplying numerator and denominator by $(\sqrt{sin2(x+h)}+\sqrt{sin2x})$

we get

= $\lim_{h\to 0}\frac{\sqrt{sin2(x+h)}-\sqrt{sin2x}}{h}×\frac{\sqrt{sin2(x+h)}+\sqrt{sin2x}}{\sqrt{sin2(x+h)}+\sqrt{sin2x}}$

= $\lim_{h\to 0}\frac{sin(2x+2h)-sin2x}{h(\sqrt{sin(2x+2h)}+\sqrt{sin2x})}$

= $\lim_{h\to 0}\frac{2cos(2x+2h)×sinh}{h}×\frac{1}{(\sqrt{sin(2x+2h)}+\sqrt{sin2x})}$

= $\frac{2cos2x}{2\sqrt{sin2x}}$

= $\frac{cos2x}{\sqrt{sin2x}}$

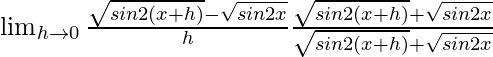
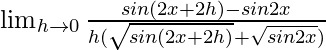
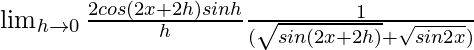
(v)sinx / x

解决方案：

Given that f{x} = sinx/x

By using the formula

$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

We get

= $\lim_{h\to 0}\frac{\frac{sin(x+h)}{x+h}-\frac{sinx}{x})}{h}$

= $\lim_{h\to 0}\frac{xsin(x+h)-(x+h)sinx}{xh(x+h)}$

= $\lim_{h\to 0}\frac{x(sinx.cosh+cosx.sinh)-x.sinx-h.sinx}{xh(x+h)}$

= $\lim_{h\to 0}\frac{x.sinx(cosh-1)}{xh(x+h)}+\frac{x.cosx.sinh}{xh(x+h)}-\frac{hsinx}{(x+h)xh}$

= $\frac{-xsinx}{x(x+h)}×\frac{2sin^2h/2}{h^2/4}×h/4+\frac{xcosx}{x^2}-\frac{sinx}{x^2}$

h ⇢ 0 ⇒ h/2 ⇢ 0 and $\lim_{θ\to 0}\frac{sinθ}{θ}=1$

= $0+\frac{xcosx-sinx}{x^2}$

=$\frac{xcosx-sinx}{x^2}$

(vi)cosx / x

解决方案：

Given that f(x) = cosx/x

By using the formula

$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

We get

= $\lim_{h\to 0}\frac{\frac{cos(x+h)}{x+h}-\frac{cosx}{x}}{h}$

= $\lim_{h\to 0}\frac{x.cos(x+h)-(x+h)cosx}{h(x+h)}$

= $\lim_{h\to 0}\frac{x[cosx.cosh-sinx.sinh]-x.cos-h.cosx}{h(x+h)}$

= $\lim_{h\to 0}\frac{xcosx(cosh-1)}{h(x+h)}-\frac{x.cosx.sinh}{(x+h)h}-\frac{h.cosx}{(x+h)h}$

= $\lim_{h\to 0}\frac{-xcosx.2sin^2(h/2)}{(x+h)\frac{h^2}{4}}\frac{h^2}{4}-\frac{xsinx}{x(x+h)}-\frac{cosx}{x(x+h)}$

= $0-\frac{xsinx}{x^2}-\frac{cosx}{x^2}$

= $-\frac{xsinx-cosx}{x^2}$

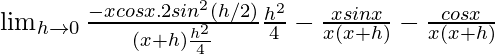
(vii)x ² sinx

解决方案：

Given that f(x) = x²sinx

By using the formula

$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

We get

= $\lim_{h\to 0}\frac{(x+h)^2sin(x+h)-x^2sinx}{h}$

= $\lim_{h\to 0}\frac{(x^2+h^2+2hx)(sinx.cosh+cosx.sinh)-x^2sinx}{h}$

= $\lim_{h\to 0}\frac{x^2sinx(cosh-1)}{h}+\frac{h(h+2x)cosh.sinx}{h}-(x+h)^2cosx\frac{sinh}{h}$

= $\lim_{h\to 0}-x^2sinx\frac{2sin^2(h/2)}{(h/2)^2}h^2/4+(h+2x)sinx.cosh+(x+h)^2cosx$

= 0 + [2xsinx + x²cosx]

= 2xsinx + x²cosx

(viii) 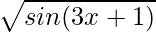$\sqrt{sin(3x+1)}$

解决方案：

Given that f(x) = $\sqrt{sin(3x+1)}$

By using the formula

$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

We get

= $\lim_{h\to 0}\frac{\sqrt{sin3(x+h)+1}-\sqrt{sin(3x+1)}}{h}$

= $\lim_{h\to 0}\frac{\sqrt{sin3(x+h)+1}-\sqrt{sin(3x+1)}}{h}\frac{\sqrt{sin3(x+h)+1}+\sqrt{sin(3x+1)}}{\sqrt{sin3(x+h)+1}+\sqrt{sin(3x+1)}}$

= $\lim_{h\to 0}\frac{sin(3x+3h+1)-sin(3x+1)}{h(\sqrt{sin3(x+h)+1}+\sqrt{sin(3x+1)})}$

= $\lim_{h\to 0}2cos(3x+1+3h/2)×\frac{sin(3h/2)}{3h/2}×3/2×\frac{1}{\sqrt{sin3(x+h)+1}+\sqrt{sin(3x+1)}}$

= $\frac{3cos(3x+1)}{2\sqrt{sin(3x+1)}}$

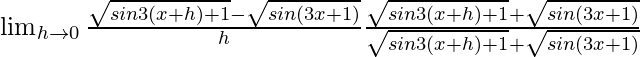
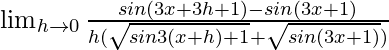
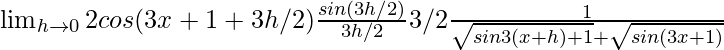
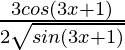
(ix)sinx + cosx

解决方案：

Given that f(x) = sinx + cosx

By using the formula

$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

We get

= $\lim_{h\to 0}\frac{[sin(x+h)+cos(x+h)]-sinx+cosx}{h}$

= $\lim_{h\to 0}\frac{[sin(x+h)+cos(x+h)-sinx-cosx]}{h}$

= $\lim_{h\to 0}\frac{[sin(x+h)-sinx]+[cos(x+h)-cosx]}{h}$

= $\lim_{h\to 0}\frac{[2sin\frac{x+h-x}{2}cos\frac{x+h+x}{2}]+[-2sin\frac{x+h+x}{2}sin\frac{x+h-x}{2}]}{h}$

= $\lim_{h\to 0}\frac{sinh.cos\frac{2x+h}{2}-2sin(x+\frac{h}{2})sinh}{h}$

= $\lim_{h\to 0}\frac{sinh}{h}[cos\frac{x+h}{2}-sin(x+\frac{h}{2})]$

= cosx – sinx

问题4.使用第一原则区分以下每个方面：

(i)棕褐色² x

解决方案：

Given that f(x) = tan²x

By using the formula

$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

We get

= $\lim_{h\to 0}\frac{tan^2(x+h)-tan^2x}{h}$

= $\lim_{h\to 0}\frac{[tan(x+h)+tanx][tan(x+h)-tanx]}{h}$

= $\lim_{h\to 0}\frac{\frac{sin(x+h+x)}{cos(x+h)cosx}×\frac{sin(x+h-x)}{cos(x+h)cosx}}{h}$

= $\lim_{h\to 0}\frac{sin(2x+h)}{cos(x+h)cosx}×\frac{sinh}{cos(x+h)cosx}$

= $\lim_{h\to 0}\frac{sinh}{h}×\frac{sin2x}{cos^2(x+h)cos^2x}$

= $\lim_{h\to 0}\frac{sin2x}{cos^2x.cos^2x}$

= $\lim_{h\to 0}\frac{2sinx.cosx}{cos^2x}×\frac{1}{cos^2x}$

= 2tanx sec²x

(ii)棕褐色(2x +1)

解决方案：

Given that f(x) = tan(2x+1)

By using the formula

$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

We get

= $\lim_{h\to 0}\frac{tan[2(x+h)+1]-tan(2x+1)}{h}$

= $\lim_{h\to 0}\frac{sin(2x+2h+1-2x-1)}{h.cos2(x+h+1)cos(2x+1)}$

= $\lim_{h\to 0}\frac{2sin2h}{2h.cos(2x+2h+1)cos(2x+1)}$

Multiplying both, numerator and denominator by 2.

= $\lim_{h\to 0}2(\frac{sin2h}{2})\frac{1}{cos(2x+2h+1)cos(2x+1)}$

= $\frac{2}{cos^2(2x+1)}$

= 2sec²(2x+1)

(iii)tan2x

解决方案：

Given that f(x) = tan2x

By using the formula

$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

We get

= $\lim_{h\to 0}\frac{tan2(x+h)-tan2x}{h}$

= $\lim_{h\to 0}\frac{sin(2x+2h-2x)}{h.cos(2x+2h)cos2x}$

= $\lim_{h\to 0}\frac{sin2h}{h.cos(2x+2h)cos2x}$

= $\lim_{h\to 0}(\frac{sin2h}{2h})×\frac{1×2}{cos(2x+2h)cos2x}$

= $\frac{2}{cos2x.cos2x}$

= 2sec²2x

(iv)√容器

解决方案：

Given that f(x) = √tanx

By using the formula

$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

We get

= $\lim_{h\to 0}\frac{\sqrt{tan(x+h)}-\sqrt{tanx}}{h}$

On multiplying numerator and denominator by ${\sqrt{tan(x+h)}+\sqrt{tanx}}$

We get

= $\lim_{h\to 0}\frac{tan(x+h)-tanx}{h(\sqrt{tan(x+h)}+\sqrt{tanx})}$

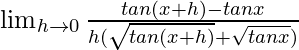
= $\lim_{h\to 0}\frac{sin(x+h-x)}{h.cos(x+h)cosx[\sqrt{tan(x+h)}+\sqrt{tanx}]}$

= $\lim_{h\to 0}\frac{sinh}{h}×\frac{1}{cos(x+h)cosx[\sqrt{tan(x+h)}+\sqrt{tanx}]}$

= $\lim_{h\to 0}\frac{1}{cos^2x.2\sqrt{tanx}}$

= $\frac{sec^2x}{2\sqrt{tanx}}$

问题5.使用第一原则区分以下每个方面：

(一世) 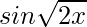$sin\sqrt{2x}$

解决方案：

Given that f(x) = $sin\sqrt{2x}$

By using the formula

$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

We get

= $\lim_{h\to 0}\frac{sin\sqrt{2(x+h)}-sin\sqrt{2x}}{h}$

= $\lim_{h\to 0}\frac{2sin[\frac{\sqrt{2(x+h)}-\sqrt{2x}}{2}]cos[\frac{\sqrt{2(x+h)}+\sqrt{2x}}{2}]}{h}$

= $\lim_{h\to 0}\frac{sin[\frac{\sqrt{2(x+h)}-\sqrt{2x}}{2}]}{[\frac{\sqrt{2(x+h)}-\sqrt{2x}}{2}]}\frac{(\sqrt{2(x+h)}-\sqrt{2x})(\sqrt{2(x+h)}+\sqrt{2x})}{(\sqrt{2(x+h)}+\sqrt{2x})h}cos[\frac{\sqrt{2(x+h)+2x}}{2}]$

= $\lim_{h\to 0}\frac{sin[\frac{\sqrt{2(x+h)}-\sqrt{2x}}{2}]}{[\frac{\sqrt{2(x+h)}-\sqrt{2x}}{2}]}\lim_{h\to 0}\frac{{2(x+h)}-2x}{(\sqrt{2(x+h)}+\sqrt{2x})h}\lim_{h\to 0}cos[\frac{\sqrt{2(x+h)+2x}}{2}]$

= $1×\frac{2}{2\sqrt{2x}}cos(\sqrt{2x})$

= $\frac{cos\sqrt{2x}}{\sqrt{2x}}$

(ii)cos√x

解决方案：

Given that f(x) = cos√x

By using the formula

$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

We get

= $\lim_{h\to 0}\frac{cos\sqrt{x+h}-cos\sqrt{x}}{h}$

= $\lim_{h\to 0}\frac{-2sin[\frac{\sqrt{x+h}+\sqrt{x}}{2}].sin[\frac{\sqrt{x+h}-\sqrt{x}}{2}]}{h}$

= $\lim_{h\to 0}\frac{-2sin[\frac{\sqrt{x+h}-\sqrt{x}}{2}][\sqrt{x+h}-\sqrt{x}[\sqrt{x+h}+\sqrt{x}]}{h[\frac{\sqrt{x+h}-\sqrt{x}}{2}][\sqrt{x+h}+\sqrt{x}]}×sin[\frac{\sqrt{x+h}+\sqrt{x}}{2}]$

Multiplying numerator and denominator by $(\sqrt{x+h}-\sqrt{x})$

= $\lim_{h\to 0}\frac{-sin[\frac{\sqrt{x+h}-\sqrt{x}}{2}]}{[\frac{\sqrt{x+h}-\sqrt{x}}{2}]}×\frac{x+h-x}{(\sqrt{x+h}+\sqrt{x})h}×sin[\frac{\sqrt{x+h}+\sqrt{x}}{2}]$

= $\lim_{h\to 0}-1\frac{h}{(\sqrt{x+h}+\sqrt{x})h}×sin[\frac{\sqrt{x+h}+\sqrt{x}}{2}]$

= $\lim_{h\to 0}\frac{-1}{(\sqrt{x+h}+\sqrt{x})}×sin\frac{\sqrt{x+h}+\sqrt{x}}{2}$

= $-\frac{sin\sqrt{x}}{2\sqrt{x}}$

(iii)tan√x

解决方案：

Given that f(x) = tan√x

By using the formula

$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

We get

= $\lim_{h\to 0}\frac{tan\sqrt{x+h}-tan\sqrt{x}}{h}$

= $\lim_{h\to 0}\frac{sin\sqrt{x+h}-\sqrt{x}}{h.cos\sqrt{x+h}cos\sqrt{x}}$

= $\lim_{h\to 0}\frac{sin\sqrt{x+h}-\sqrt{x}}{(x+h-x)cos\sqrt{x}.cos\sqrt{x+h}}$

= $\lim_{h\to 0}\frac{sin(\sqrt{x+h}-\sqrt{x})}{(\sqrt{x+h}-\sqrt{x})(\sqrt{x+h}+\sqrt{x})cos\sqrt{x}.cos\sqrt{x+h}}$

= $\lim_{h\to 0}\frac{sin(\sqrt{x+h}-\sqrt{x})}{(\sqrt{x+h}-\sqrt{x)}}×\frac{1}{(\sqrt{x+h}+\sqrt{x})cos\sqrt{x}.cos\sqrt{x+h}}$

= $1×\frac{1}{2\sqrt{x}.cos\sqrt{x}.cos\sqrt{x+h}}$

= $\frac{1}{2\sqrt{x}cos^2x}$

= $\frac{sec^2\sqrt{x}}{2\sqrt{x}}$

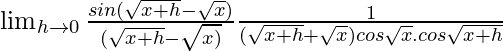
(iv)tanx ²

解决方案：

Given that f(x) = tanx²

By using the formula

$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

We get

= $\lim_{h\to 0}\frac{tan(x+h)^2-tanx^2}{h}$

= $\lim_{h\to 0}\frac{\frac{sin(x+h)^2}{cos(x+h)^2}-\frac{sinx^2}{cosx^2}}{h}$

= $\lim_{h\to 0}\frac{\frac{sin(x+h)^2cosx^2-cos(x+h)^2sinx^2}{{cos(x+h)^2}cosx^2}}{h}$

= $\lim_{h\to 0}\frac{sin((x+h)^2-x^2)}{h.{cos(x+h)^2}.cosx^2}$

= $\lim_{h\to 0}\frac{sin(x^2+h^2+2hx-x^2)}{h.{cos(x+h)^2}.cosx^2}$

= $\lim_{h\to 0}\frac{sin(h^2+2hx)}{h.{cos(x+h)^2}.cosx^2}$

= $\lim_{h\to 0}\frac{sinh}{h}×\frac{(h+2x)}{{cos(x+h)^2}.cosx^2}$

= $1.\frac{2x}{cos^2(x)^2}$

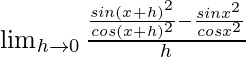
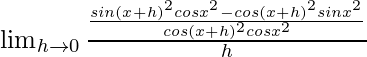
= 2xsec²x²

问题6.使用第一原则区分以下每个方面：

(i)-x

解决方案：

Given that f(x) = -x

By using the formula

$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

We get

= $\lim_{h\to 0}\frac{-(x+h)+x}{h}$

= $\lim_{h\to 0}\frac{-x-h+x}{h}$

= -1

(ii)(-x) ^-1

解决方案：

Given that f(x) = (-x)^-1

By using the formula

$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

We get

= $\lim_{h\to 0}\frac{\frac{-1}{x+h}+\frac{1}{x}}{h}$

= $\lim_{h\to 0}\frac{-x+x+h}{hx(x+h)}$

= $\lim_{h\to 0}\frac{1}{x^2+xh}$

= 1/x²

(iii)罪(x +1)

解决方案：

Given that f(x) = sin(x+1)

By using the formula

$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

We get

= $\lim_{h\to 0}\frac{sin(x+h+1)-sin(x+1)}{h}$

= $\lim_{h\to 0}\frac{2cos(\frac{x+h+1+x+1}{2})sin(\frac{x+h+1-x-1}{2})}{h}$

= $\lim_{h\to 0}\frac{2cos(\frac{2x+2+h}{2})sin(\frac{h}{2})}{h}$

= $\lim_{h\to 0}cos(\frac{2x+2+h}{2})(\frac{sin(h/2)}{h/2})$

= $cos(\frac{2(x+1)}{2})$

= cos(x+1)

(iv)cos(x –π/ 8)

解决方案：

We have, f(x) = cos(x – π/8)

By using the formula

$f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

We get

= $\lim_{h\to 0}\frac{cos(x+h-π/8)-cos(x-π/8)}{h}$

= $\lim_{h\to 0}-2sin\frac{sin(\frac{2x+h-2π/8}{2})-sin(\frac{h+x-π/8-x+π/8}{2})}{h}$

= $\lim_{h\to 0}\frac{-2sin(\frac{2x+h-2π/8}{2})sin(h/2)}{2.h/2}$

= $\lim_{h\to 0}\frac{-2sin(\frac{2x+h-2π/8}{2})}{2}\lim_{h\to 0}\frac{sin(h/2)}{h/2}$

= $\lim_{h\to 0}sin(\frac{2x+h-2π/8}{2})$

= $sin(\frac{2x-2π/8}{2})$

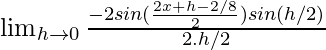
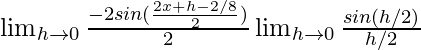
= -sin(x + π/8)