12类RD Sharma解决方案-第30章线性编程–练习30.1 |套装2

问题11：两名裁缝A和B的日薪分别为150卢比和200卢比。 A每天可以缝制6件衬衫和4条裤子，而B可以每天缝制衬衫和4条裤子。形成线性规划问题，以最小化生产至少60件衬衫和32条裤子的人工成本。

回答：

The above LPP can be represented in the table above.

To minimize labour cost means to assume minimize the earnings, i.e, Min Z = 150x + 200y such that the constraints

x>=0; y >= 0  (at least 1 shirt and pant is required)

6x + 10y >= 60  (require at least 60 shirts)

4x + 4y >= 32  (require at least 32 pants)

Solving the above inequalities a s equations we get, x = 5 and y = 3

Other corner points obtained are (0, 6) & (10, 0), (0, 8) & (8, 0)

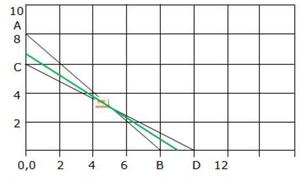
The feasible region is the open unbounded region A-E-D.

Point E(5, 3) may not be the minimal value. So, plot 150x + 200y < 1350 to see if there is a common region with A-E-D.

The green line has no common point, therefore

Stitching 5 shirts and 3 pants minimizes labour cost to Rs. 1350.

问题12.一家航空公司同意为一个团体包机。该团体至少需要160个头等舱座位和至少300个游客舱位。警长必须使用其314型飞机中的至少两个，这些飞机有20个头等舱座位和30个游客舱位。该航空公司还将使用其535型飞机中的某些飞机，这些飞机有20个头等舱座位和60个游客座位。 314型飞机的每次飞行花费公司10万卢比，而535型飞机的每次飞行花费15万卢比。为了减少飞行成本，每种类型的飞机应使用多少架?将其表述为LPP。

给定的信息可以制成表格，如下所示：

	Taylor A		Taylor B	Limit
Variable	x	+	y
Shirts	6x	+	10y	>=60
Pants	4x	+	4y	>=32
Earn Rs	150	+	200	Z

回答：

	Model 314		Model 535	Limit
Variable	x	+	y
F class	20x	+	20y	>= 160
T class	30x	+	60y	>= 300
Cost	x lakh	+	1.5y lakh	Z

The above LPP can be represented in the table above.

The flight cost is to be minimized, i.e, Min Z = x +1.5y such that the constraints

x >= 2  (at least 2 planes of model 314 must be used)

y >= 0  (at least 1 planes of model 535 must be used)

20x + 20y >= 160  (require at least 160F class seats)

30x + 60y >= 300  (require at least 300T class seats)

Solving the above inequalities as equations we get,

When x = 0, y = 8 and when y = 0, x = 8

When x = 0, y = 5 and when y = 0, x = 10

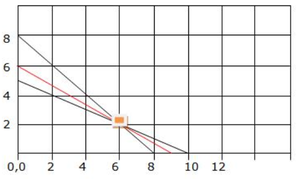
We get an unbounded region 8-E-10 as a feasible solution. Plotting the corner points and evaluating we have, 

Corner point	Value of Z = x + 1.5y
10, 0	10
0, 8	12
6, 2	9

Since we obtained an unbounded region as the feasible solution a plot of Z ( x + 1.5y < 9) is plotted.

since there are no common points , point E is the point that gives the minimum value.

Using 6 planes of model 314 & 2 of model 535 gives minimum cost of 9 lakh rupees.

问题13。阿米特(Amit)的数学老师给了他三道很长的问题清单，并指示他们提交不超过100个(正确解决的)问题才能获得学分。第一组中的问题每人得5分，第二组中的问题每人得4分，第三组中的问题每人得6分。 Amt从经验中知道，他平均需要3分钟才能解决5分问题，需要2分钟才能解决4分问题，并且需要4分钟才能解决6分问题。由于他还有其他问题要担心，因此他不能花全部3.5个小时以上的时间从事数学作业。此外，前两组问题涉及数值计算，并且他知道他不能忍受超过2.5个小时的时间来处理此类问题。在这种情况下，为了使自己的努力获得最大可能的信誉，他应该在每个类别中解决多少个问题?将其表述为LPP。

回答：

Given information can be tabulated as below

Sets	Time requirement	Points
1	3	5
2	2
3	4	6
Time for all three sets = 3.5 hours Time for Set 1 ans Set 2 = 2.5 hours Maximum number of questions = 100

Let there be x, y, z questions from set 1, 2 and 3 respectively.

Given, each question from set 1, 2 and 3 earn 5,4 and 6 points respectively. So x questions of set 1, y questions of set 2 and z questions of set 3 earn 5x, 4y and 6z points.

Let total point credit be U

So, U = 5x + 4y + 6z

Given, each questions of set 1, 2 and 3 require 3, 2 and 4 minutes respectively. So, x questions of set 1, y questions of set 2 and z questions of set 3 require 3x, 2y and 4z minutes respectively but given that total time to devote in all three sets is 3.5 hours = 210 minutes and the first two sets is 2.5 hours = 150 minutes.

So, 

3x + 2y + 4z <= 210 (First constraint)

3x + 2y < =150  (Second constraint)

Given, total number of questions cannot exceed 100.

So, x + y + z <= 100   (Third constraint)

Hence, mathematical formulation of LPP is

Find x and y which maximize U = 5x + 4y + 6z

Subject to constraint, 

3x + 2y + 4z <= 210

3x + 2y < =150

x + y + z <= 100

x, y, z >= 0 (Since number of questions to solve from each set cannot be less than zero)

问题14.一个农民有一个100英亩的农场。他可以卖他可以养的西红柿，生菜或萝卜。他可以获得的价格是西红柿每公斤Re 1，莴苣每头0.75卢比，萝卜每公斤2卢比。每英亩萝卜的平均产量为2000公斤，莴苣为3000头，萝卜为1000公斤。肥料的价格为每公斤0.05卢比，西红柿和生菜每英亩所需量为100公斤，萝卜为50公斤。每英亩播种，栽培和收获所需的劳动力是西红柿和萝卜5个人日，生菜6个人日。总共有400个工作日的劳动，每人每天20卢比。将此问题表述为LPP，以最大限度地提高农民的总利润。

回答：

Given information can be tabulated as below:

Product	Yield	Cultivation	Price	Fertilizers
Tomatoes	2000 kg	5 days	1	100 kg
Lettuce	3000 kg	6 days	0.75	100 kg
Radishes	1000 kg	5 days	2	50 kg

Average 2000 kg/per acre

Total land = 100 Acre

Cost of fertilizers = Rs 0.50 per kg

A total of 400 days of cultivation labour with Rs 20 per day

Let required quantity of field for tomatoes, lettuce and radishes be x, y and z acre respectively.

Given, costs of cultivation and harvesting of tomatoes, lettuce and radishes are 5 * 20 = Rs 100, 6 * 20 = Rs 120, 5 * 20 = Rs 100 respectively per acre. Cost of fertilizers for tomatoes, lettuce and radishes 100 * 0.05 = Rs 50, 100 * 0.50 = Rs 50 ans 50 * 0.50 = Rs 25 respectively per acre.

So, total costs of production of tomatoes, lettuce and radishes are Rs 100 + 50 = Rs 150x, Rs 120 + 50 = Rs 170y and Rs 100 + 25 = Rs 125z respectively. Total selling price of tomatoes, lettuce according to yield are 2000 * 1 = Rs 2000x, 3000 * 0.75 = Rs 2250y and 1000 * 2 = Rs 2000z respectively.

Let U be the total profit,

So, 

U = (2000x – 150x) + (2250y – 170y) + (2000z – 125z)

U = 1850x + 2080y + 1875z

Given, farmer has 100 acre from

So, x + y + z <= 100 (First constraint)

Number of cultivation and harvesting days are 400

So, 5x + 6y + 5z <= 400  (Second constraint)

Hence, mathematical formulation of LPP is

Find x, y, z which maximize U = 11850x + 2080y + 1875z

Subject to constraint,

 x + y + z <= 100

5x + 6y + 5z <= 400

x, y, z >=0  (Since cultivation cannot be less than zero)

问题15.一个公司生产两种产品，每种产品必须通过两个部门1和2进行处理。每个部门中每个产品的每小时需求，每个部门的每周生产能力，每单位的销售价格，每单位的人工成本单位和原材料成本汇总如下：

Corner point	Value of Z = 150x + 200y
0, 8	0
10, 0	1500
5, 3	1350

问题是确定生产每种产品的单位数量，以使对利润的总贡献最大化。将其表述为LPP。

回答：

Given information can be tabulated as below:

Product	Department 1	Department 2	Selling price	Labour cost	Raw material cost
A	3	4	25	16	4
B	2	6	30	20	4
Capacity	130	260

Let the required number of product A and B be x and y units respectively.

Given, labour cost and raw material cost of one unit of product A is Rs 16 and Rs 4, so total cost of product A is Rs 16 + Rs 4 = Rs 20

And given selling price of 1 unit of product A is Rs 25

So, profit on one unit of product A = Rs 25 – Rs 20 = Rs 5

Again,  labour cost and raw material cost of one unit of product A is Rs 20 and Rs 4, so total cost of product A is Rs 20 + Rs 4 = Rs 24

And given selling price of 1 unit of product B is Rs 30

So, profit on one unit of product B = Rs 30 – Rs 24 = Rs 6

Hence, profits on x unit of product A and y units of product B are Rs 5x and Rs 6y respectively.

Let Z be the total profit, so Z = 5x + 6y

Given, production of one unit of product A and B need to process for 3 and 4 hours respectively in department 1, so production of x units of product A and y units of product B need to process for 3x and 4y hours respectively in department 1. But total capacity of Department 1 is 130 hours,

So, 3x + 2y <= 130  (First Constraint)

Given, production of one unit of product A and B need to process for 4 and 6 hours respectively in department 2, so production of x units of product A and y units of product B need to process for 4x and 6y hours respectively in department 2. But total capacity of Department 2 is 260 hours,

So, 4x + 6y <= 260  (Second Constraint)

Hence, mathematical formulation of LPP is

Find x, y, z which maximize Z = 5x + 6y

Subject to constraint, 

3x + 2y <= 130

4x + 6y <= 260

x, y >= 0 (Since production cannot be less than zero)