第12类RD Sharma解决方案–第30章线性编程–练习30.5

问题1.两个仓库A和B的增益能力分别为100公担和50公担。他们向3个口粮商店D，E和F供应，分别需要60、50和40公担。下表列出了从仓库到商店的每公担运输成本：

Transportation cost per quintal (in Rs)
From/ To	A	B
D	6	4
E	3	2
F	2.50	3

为了使运输成本最低，应如何运输补给品?最低费用是多少?

解决方案：

Let us assume godown A supply x and y quintals of grain to the shops D and E.

Afterwards, (100 – x – y) will be supplied to shop F.

The requirement at shop D is 60 quintals 

Since, x quintals are transported from godown A.

Therefore, the remaining (60 − x) quintals will be transported from godown B.

Similarly, 

(50 − y) quintals and 40 − (100 − x − y) i.e. (x + y − 60) quintals will be transported from godown B to shop E and F respectively.

The diagrammatic representation of the given problem:

x ≥ 0 , y ≥ 0 and 100 – x – y ≥ 0  

⇒ x ≥ 0 , y ≥ 0 , and x + y ≤ 100

60 – x ≥ 0 , 50 – y ≥ 0 , and x + y – 60 ≥ 0

⇒ x ≤ 60 , y ≤ 50 , and x + y ≥ 60  

Total transportation cost Z is given by,

Z = 6x + 3y + 2.5(100 – x – y) + 4(60 – x) + 2(50 – y) + 3( x + y – 60)

= 6x + 3y + 250 – 2.5x – 2.5y + 240 – 4x + 100 – 2y + 3x + 3y – 180

= 2.5x + 1.5y + 410

Thus, the required mathematical formulation of linear programming is:

Minimize Z = 2.5x + 1.5y + 410  

subject to the constraints,

x + y ≤ 100

x ≤ 60

y ≤ 50

x + y ≥ 60

x, y ≥ 0

The feasible region obtained by the system of constraints is:

The corner points are A(60, 0), B(60, 40), C(50, 50), and D(10, 50).

The values of Z at these corner points are given below.

Therefore, 

The minimum value of Z is 510 at D (10, 50).

Hence, the amount of grain transported from A to D, E, and F is 10 quintals, 50 quintals, and 40 quintals respectively.

From B to D, E, and F is 50 quintals, 0 quintals, and 0 quintals respectively.

The minimum cost is Rs 510.

问题2.一家医疗公司在A和B两个地方都设有工厂。从这两个地方开始分别向位于P，Q和R的三个机构提供产品。这些机构的每月需求分别为40、40和50包，而工厂的生产能力A和B分别为60和70包。从工厂到代理商的每包运输成本如下：

Corner point	Z = 2.5x + 1.5y + 410
A (60, 0)	560
B (60, 40)	620
C (50, 50)	610
D (10, 50)	510 -> minimum

每个工厂要从多少个小包运输到每个代理商，以使运输成本最低?另外，找到最低费用?

解决方案：

The diagrammatic representation of the given problem:

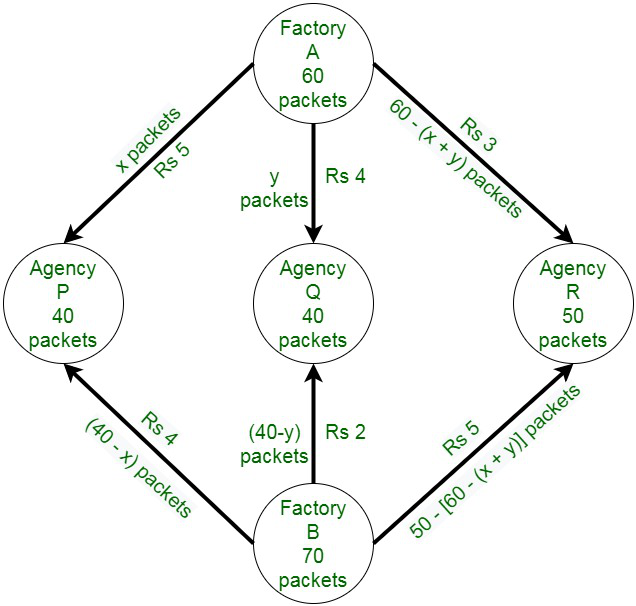
Assume x and y packets be transported from factory A to the agencies P and Q respectively.  

After that, 

[60 − (x + y)] packets be transported to the agency R.

First constraint ⇢  x, y ≥ 0 and

Second constraint ⇢ 60 − (x + y) ≥ 0

(x + y) ≤ 60

The requirement at agency P is 40 packets. 

Since, x packets are transported from factory A,  

Therefore, the remaining (40 − x) packets are transported from factory B.

Similarly, 

(40 − y) packets are transported by B to Q and 50− [60 − (x + y)] 

i.e. (x + y − 10) packets will be transported from factory B to agency R respectively.

Number of packets cannot be negative.

Hence,

Third constraint ⇢ 40 – x ≥ 0

=> x ≤ 40

Fourth constraint ⇢ 40 – y ≥ 0

=> y ≤ 40

Fifth constraint ⇢ x + y – 10 ≥ 0

=> x + y ≥ 10

Thus, 

Costs of transportation of each packet from factory A to agency P, Q, R are Rs 5, 4, 3.

Costs of transportation of each packet from factory B to agency P, Q, R are Rs 4, 2, 5.

Let total cost of transportation be Z.

Z = 5x + 4y + 3[60 – x + y] + 4(40 – x) + 2(40 – y) + 5(x + y – 10]

= 3x + 4y + 10

Hence, 

The required mathematical formulation of linear programming is:

Minimize Z = 3x + 4y + 370

subject to constraints,

x + y ≤ 60

x ≤ 40

y ≤ 40

x + y ≥ 10

where, x, y ≥ 0

Let us convert inequations into equations as follows:

x + y = 60, x = 40, y = 40, x + y = 10, x = 0 and y = 0

Region represented by x + y ≤ 60:

The line x + y = 60 meets the coordinate axes at A₁ (60, 0) and B₁ (0, 60) respectively. 

Region containing origin represents x + y ≤ 60 as (0, 0) satisfies x + y ≤ 60.

Region represented by x ≤ 40:

The line x = 40 is parallel to y-axis, meets x-axis at A₂ (40, 0). Region containing origin represents x ≤ 40 as (0, 0) satisfies x ≤ 40.

Region represented by y ≤ 40:

The line y = 40 is parallel to x-axis, meets y-axis at B₂ (0, 40). 

Region containing origin represents y ≤ 40 as (0, 0) satisfies y ≤ 40.

Region represented by x + y ≥ 10:

The line x + y = 10 meets the coordinate axes at A₂ (10, 0) and B₃ (0, 10) respectively. 

Region not containing origin represents x + y ≥ 10 as (0, 0) does not satisfy x + y ≥ 10.

Shaded region A₃ A₂ P Q B₂ B₃ represents feasible region.

Point P(40, 20) is obtained by solving x = 40 and x + y = 60

Point Q(20, 40) is obtained by solving y = 40 and x + y = 60

The value of Z = 3x + 4y + 370 at

A₃(10, 0) = 3(10) + 4(0) + 370 = 400

A₂(40, 0) = 3(40) + 4(0) + 370 = 490

P(40, 20) = 3(40) + 4(20) + 370 = 570

Q(20, 40) = 3(20) + 4(40) + 370 = 590

B₂(0, 40) = 3(0) + 4(40) + 370 = 530

B₃(0, 10) = 3(0) + 4(10) + 370 = 410

Hence, minimum value of Z = 400 at x = 10, y = 0

So, 

From A -> P = 10 packets

From A -> Q = 0 packets

From A -> R = 50 packets

From B -> P = 30 packets

From B -> Q = 40 packets

From B -> R = 0 packets

Therefore, minimum cost = Rs 400