第12类RD Sharma解–第22章微分方程–练习22.11 |套装3

问题23.在曲线的每个点上，斜率是横坐标与纵坐标与横坐标乘积的和，曲线通过(0，1)求曲线的方程。

解决方案：

Slope is given by, (dy/dx)

We have,

(dy/dx) = x + xy

(dy/dx) = x(y + 1)

dy/(y + 1) = xdx

On integrating both sides, we get

∫dy/(y + 1) = ∫xdx

Log|y + 1| = (x²/2) + c       …(i)

Since the curve is passing through (0, 1)

Log|2| = c

Log|y + 1| = (x²/2) + Log|2|

Log|(y + 1)/2| = x²/2

$\frac{y+1}{2}=e^{\frac{x^2}{2}}$

$y+1=2e^{\frac{x^2}{2}}$

问题24.一条曲线使得从该曲线的任意点的切线的原点开始的垂线的长度等于P的横坐标。证明该曲线的微分方程为y ² – 2xy(dy / dx) – x ² = 0，因此找到曲线。

解决方案：

Tangent of the curve is given by,

Y – y = (dy/dx)(X – x)

If P be perpendicular from the origin, then

$P=\frac{x\frac{dy}{dx}-y}{\sqrt{1+(\frac{dy}{dx})^2}}=x$

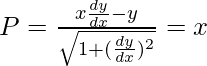
x²(dy/dx)² – 2xy(dy/dx) + y² = x² + x²(dy/dx)²

y² – 2xy(dy/dx) – x² = 0

Hence Proved.

Now we find the curve

So, weh have y² – 2xy(dy/dx) – x² = 0

(dy/dx) = (y² – x²)/2xy

Above equation is homogenous equation.

Let, y = vx

On differentiating both sides we have,

(dy/dx) = v + x(dv/dx)

v + x(dv/dx) = (v²x² – x2)/2xvx

v + x(dv/dx) = (v² – 1)/2v

x(dv/dx) = [(v² – 1)/2v] – v

x(dv/dx) = (v² – 1 – 2v²)/2v

x(dv/dx) = -(1 + v²)/2v

2vdv/(1 + v²) = -(dx/x)

On integrating both sides

∫2vdv/(1 + v²) = -∫(dx/x)

log|1 + v²| = -log|x| + log|c|

log|x(1 + v²)| = log|c|

x(1 + y²/x²) = c

(x² + y²) = cx

问题25.找到通过点(1、2)的曲线方程，并且接触点纵坐标的脚与切线与x轴的交点之间的距离是横坐标的两倍。联络点。

解决方案：

Let us considered 

the point of contact of tangent = P(x, y)

and the curve is y = f(x).

The equation of tangent of the curve is given by,

Y – y = (dy/dx)(X – x) 

Where (X, Y) is arbitrary point on the tangent.

Putting Y = 0,

0 – y = (dy/dx)(X – x)

(X – x) = -y(dx/dy)

X = x – y(dx/dy)

Coordinates at contact of x-axis = [x – y(dx/dy), 0]

The distance between the foot of the ordinate of the point of 

contact and the point of intersection of the tangent with x-axis is equal to 2x.

$\sqrt{(x-y\frac{dx}{dy}-x)^2+(0)^2}=2x$

y(dx/dy) = 2x

(dx/x) = 2(dy/y)

On integrating both sides

∫(dx/x) = 2∫(dy/y)

log|x| = 2log|y| + log|c|        …(i)

Curve is passing through (1, 2)

log|1| = 2log|2| + log|c|

log|c| = -2log|2|

On putting the value of log|c| in equation (i)

log|x| = 2log|y| – 2log|2|

log|x| = log|y²/4|

x = (y²/4)

y² = 4x

问题26.给定曲线的每个点的法线是曲线上的(x，y)穿过点(3，0)。如果曲线包含点(3，4)。找到它的方程式。

解决方案：

Let us considered the point on the curve = P(x, y). 

The equation of tangent of the curve is given by,

Y – y = -(dx/dy)(X – x)         …(i)

It passes through (3, 0) So,

0 – y = -(dx/dy)(3 – x)

ydy = 3dx – xdx

On integrating both sides

∫ydy = 3∫dx – ∫xdx

(y²/2) = 3x – (x²/2) + c

It passes through (3, 4)

(16/2) = 9 – (9/2) + c           …(ii)

c = (16/2) – (9/2)

c = (7/2)

(y²/2) = 3x – (x²/2) + (7/2)

or

y² = 6x – x² + 7

问题27.培养物中细菌的生长速率与存在的细菌数量成正比，并且发现细菌数量在6小时内增加了一倍。证明细菌在18小时结束时变成8次。

解决方案：

Let us considered 

the initial count of bacteria = P₀

the count of bacteria at a particular time ‘t’ = P 

and the growth of bacteria = g times.

We have,

dP/dt ∝ P

dP/dt = gP

dP/P = gdt

On integrating both sides

∫(dP/P) = g∫dt

Log|P| = gt + c

At t = 0, P = P₀

log|P₀| = c

Log|P| = gt + log|P₀|

Log|P/P₀| = gt

Count of bacteria becomes doubled in 6 hours.

At t = 6, P = 2P₀

Log|2P₀/P₀| = 6g

g = Log|2|/6

Log|P/P₀| = [Log|2|/6] × t

After t = 18 hours count of bacteria is equal to

Log|P/P₀| = [Log|2|/6] × 18

Log|P/P₀| = 3Log|2|

Log|P/P0| = Log|2|³

(P/P₀) = 8

P = 8P₀

Hence proved

问题28.镭的分解速率与镭的存在量成正比。发现在25年中，一定数量的镭中约有1.1％分解了。确定将原来的一半镭分解大约需要多长时间?

解决方案：

Let us considered 

the original amount of radium = P₀

and the amount of radium at a particular time ‘t’ = P

We have,

dP/dt ∝ P

(dP/dt) = -kP  (Where k is proportional constant)

(dP/P) = -kdt

On integrating both sides

∫(dP/P) = -∫kdt

Log|P| = -kt + c       …(i)

At t = 0, P = P₀

Log|P₀| = 0 + c

c = log|P₀|

Log|P| = -kt + Log|P₀|

Log|P/P₀| = -kt         …(ii)

According to the question,

In 25 years bacteria decomposes 1.1%. 

So, P = (100 – 1.1)%P₀

P = 0.989P₀

Log|P/P₀| = -kt

Log|0.989| = -25k

k = -(1/25)Log|0.989|

On putting the value of k in equation (ii)

Log|P/P₀| = (1/25)Log|0.989| × t

Time ‘T’ for one-half of the original amount of radium(i.e., P₀ = P/2)

Log|P₀/(P₀/2)| = (1/25)Log|0.989| × t

Log|2| = (1/25)Log|0.989| × t

t = (25Log|2|/Log|0.989|)

t = (25×0.69311)/(0.01106)

t = 1566.70

t = 1567 years 

问题29.证明在其任意点(x，y)处的斜率为(x ² + y ² )/ 2xy的所有曲线均为矩形双曲线。

解决方案：

We have,

(dy/dx) = (x² + y²)/2xy

The given equation is a homogenous equation,

So, let us considered, y = vx

On differentiating both sides we have,

(dy/dx) = v + x(dv/dx)

(dy/dx) = (x² + v²x²)/2xvx

v + x(dv/dx) = (x² + v²x²)/2xvx

v + x(dv/dx) = (1 + v²)/2v

x(dv/dx) = [(1 + v²)/2v] – v

x(dv/dx) = (1 + v² – 2v²)/2v

x(dv/dx) = (1 – v²)/2v

2vdv/(1 – v²) = (dx/x)

On integrating both sides

∫2vdv/(1 – v²) = ∫(dx/x)

-log|1 – v²| = log|x| – log|c|

-log|(1 – v²)| = -[log|c| – log|x|]

-log|(1 – v²)| = -log|c/x|

(1 – v²) = c/x

(1 – y²/x²) = c/x

(x² – y²)/x² = c/x

(x² – y²) = cx

This is the required equation of a rectangular hyperbola.

问题30.曲线的每个点的切线斜率等于该点的坐标之和。找到穿过原点的曲线。

解决方案：

The equation of tangent of the curve is given by,

(dy/dx) = x + y

(dy/dx) – y = x

The given equation is a linear differential equation of the form

(dx/dy) + Px = Q

Where, P = -1, Q = -x

So, I.F = e^∫Pdx

= e^∫-dx

= e^-x

The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx+c

y(e^-x) = ∫(x).(e^-x)dy+c

y(e^-x) = x∫e^-xdx-∫{(dx/dx)∫e^-xdx}dx+c

y(e^-x) = -xe^-xx + ∫e^-x + c

y(e^-x) = -xe^-x – e^-x + c

y(e^-x) = -e^-x(x + 1) + c      (i)

Since the curve is passing through origin. So,

0 = -e^-0(1) + c

c = 1

On putting the value of c in equation (i)

y(e^-x) = -e^-x(x + 1) + c

(x + y + 1) = c.e^x

Put c = 1

x + y + 1 = e^x

问题31.如果与当前点相切的斜率等于横坐标和横坐标乘积与该点的纵坐标之和，则求出通过点(0，1)的曲线方程。

解决方案：

The equation of tangent of the curve is given by

(dy/dx) = x + xy

(dy/dx) – xy = x

The given equation is a linear differential equation of the form

(dx/dy) + Px = Q

Where, P = -x, Q = x

So, I.F = e^∫Pdx

= e^-∫xdx

$=e^{-\frac{x^2}{2}}$

The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx + c

$ye^{-\frac{x^2}{2}}=∫xe^{-\frac{x^2}{2}}dx+c$

Let,

$I=∫xe^{-\frac{x^2}{2}}dx$

Let,x²/2 = z

On differentiating both sides,

xdx = dz

I = ∫e^-zdz

I = -e^-z

So,

$ye^{-\frac{x^2}{2}}=-e^{-\frac{x^2}{2}}+c$

Curve is passing through point (0, 1).

1e⁰ = -e⁰ + c

c = 2

$ye^{-\frac{x^2}{2}}=-e^{-\frac{x^2}{2}}+2$

$y=-1+2e^{\frac{x^2}{2}}$

问题32.曲线在每个点处的斜率等于该点的横坐标的平方。找到通过点(-1，1)的特定曲线。

解决方案：

According to the question,

(dy/dx) = x² 

dy = x²dx

On integrating both sides

∫dy = ∫x²dx

y = (x³/3) + c         …(i)

Curve is passing through the point (-1, 1)

1 = -(1/3) + c

c = (4/3)

On putting the value of c in equation (i)

y = (x³/3) + (4/3)

3y = x³ + 4

问题33.找到通过点(0，a)的曲线方程，这样就在点上的任意点(x，y)上，其斜率与纵坐标的乘积等于横坐标。

解决方案：

According to the question,

y(dy/dx) = x

dy = x2dx

On integrating both sides

∫ydy = ∫xdx

(y²/2) = (x²/2) + c         …(i)

Curve is passing through the point (0, a)

(a²/2) = c

c = a²/2

On putting the value of c in equation (i)

(y²/2) = (x²/2) + (a²/2)

x² – y² = -a²

问题34.曲线的切线的x截距等于点接触的纵坐标。找到通过点(1，1)的特定曲线。

解决方案：

Slop at any point is given by P = (dy/dx)

According to the question,

Slop at any point is equal to ordinate 

We have,

(dy/dx) = y

dy/y = dx

On integrating both sides

∫(dy/y) = ∫(dx)

log|y| = x + log|c|

log|y| = log|e^x| + log|c|

y = c.e^x            …(i)

Curve is passing through the point (1, 1)

1 = c.e

c = e^-1

On putting the value of c in equation (i)

y = e^x.e^-1

y = e^(x-1)