第12类RD Sharma解–第22章微分方程–练习22.9 |套装2

问题14. 3x ² dy =(3xy + y ² )dx

解决方案：

We have,

3x²dy = (3xy + y²)dx

(dy/dx) = (3xy + y²)/3x²

It is a homogeneous equation,

So put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = (3xvx + v²x²)/3x²

v + x(dv/dx) = (3v + v²)/3

x(dv/dx) = [(3v + v²)/3] – v

x(dv/dx) = (3v + v² – 3v)/3

3(dv/v²) = (dx/x)

On integrating both sides,

3∫(dv/v²) = ∫(dx/x)

-(3/v) = log|x| + c

-3x/y = log(x) + c  (Where ‘c’ is integration constant)

问题15((dy / dx)= x /(2y + x)

解决方案：

We have,

(dy/dx) = x/(2y + x)

It is a homogeneous equation,

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = x/(2vx + x)

v + x(dv/dx) = 1/(2v + 1)

x(dv/dx) = [1/(2v + 1)] – v

x(dv/dx) = (1 – 2v² – v)/(2v + 1)

(2v + 1)dv/(2v² + v – 1) = -(dx/x)

On integrating both sides,

∫(2v + 1)dv/(2v² + v – 1) = -∫(dx/x)

$∫\frac{2v+1}{2v(v+1)-1(v+1)}dx=-∫\frac{dx}{x}$

$∫\frac{2v+1}{(v+1)(2v-1)}dx=-∫\frac{dx}{x}$

Solving by partial fraction,

$\frac{2v+1}{(v+1)(2v-1)}=\frac{A}{(2v-1)}+\frac{B}{(v+1)}$

A(v + 1) + B(2v – 1) = (2v + 1)           (i)

Putting v = -1 and solve above equation,

A(0) + B(-3) = (-1)

B = (1/3)

Putting v = -(1/2) and solve equation (i),

A(3/2) + B(0) = 2

A = (4/3)

$\frac{4}{3}∫\frac{dv}{(2v-1)}+\frac{1}{3}∫\frac{dv}{(v+1)}=-log|x|+log|c|$

(3/2)log|2v – 1| + (1/3)log|v + 1| = -log|x| + log|c|

log|(2v – 1)²(v + 1)| = -log|x|³ + log|c|

|(2v – 1)²(v + 1)| = (c/x³)

(2y/x – 1)²(y/x + 1) = (c/x³)

$\frac{(2y-x)^2(x+y)}{x^2x}=\frac{c}{x^3}$

(2y – x)²(x + y) = c  (Where ‘c’ is integration constant)

问题16.(x + 2y)dx –(2x – y)dy = 0

解决方案：

We have,

(x + 2y)dx – (2x – y)dy = 0

(dy/dx) = (x + 2y)/(2x – y)

It is a homogeneous equation,  

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = (x + 2vx)/(2x – vx)

v + x(dv/dx) = (1 + 2v)/(2 – v)

x(dv/dx) = [(1 + 2v)/(2 – v)] – v

x(dv/dx) = (1 + 2v – 2v + v²)/(2 – v)

(2 – v)dv/(1 + v²) = (dx/x)

On integrating both sides,

∫(2 – v)dv/(1 + v²) = ∫(dx/x)

2∫dv/(1 + v²) – ∫vdv/(1 + v²) = log|x| + log|c|

2tan^-1v – (1/2)∫2vdv/(1 + v²) = log|x| + log|c|

2tan^-1v – log|1 + v²|^1/2 = log|cx|

2tan^-1v = log|cx√(1 + v²)|

$e^{2tan^{-1}(\frac{y}{x})}=\frac{(y^2+x^2)^{\frac{1}{2}}}{x}xc$

$e^{2tan^{-1}(\frac{y}{x})}={(y^2+x^2)^{\frac{1}{2}}}c$  (Where ‘c’ is integration constant)

问题17。 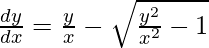$\frac{dy}{dx}=\frac{y}{x}-\sqrt{\frac{y^2}{x^2}-1}$

解决方案：

We have,

$\frac{dy}{dx}=\frac{y}{x}-\sqrt{\frac{y^2}{x^2}-1}$

It is a homogeneous equation,

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = (vx/x) – √(v²x²/x² – 1)

v + x(dv/dx) = v – √(v² – 1)

x(dv/dx) = -√(v² – 1)

dv/√(v² – 1) = -(dx/x)

On integrating both sides,

∫dv/√(v² – 1) = -∫(dx/x)

log|v + √(v² – 1)| = -log|x| + log|c|

|v + √(v² – 1)| = (c/x)

$\frac{y}{x}-[\sqrt{(\frac{y}{x})^2-1}]x=c$

y + √(y² – x²) = c  (Where ‘c’ is integration constant)

问题18.(dy / dx)=(y / x){log(y)– log(x)+ 1}

解决方案：

We have,

(dy/dx) = (y/x){log(y) – log(x) + 1}

(dy/dx) = (y/x){log(y/x) + 1}

It is a homogeneous equation,

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = v{log(v) + 1}

v + x(dv/dx) = vlog(v) + v

x(dv/dx) = vlog(v)

dv/vlogv = (dx/x)

On integrating both sides,

∫dv/vlogv = ∫(dx/x)

Let, logv = z

On differentiating both sides,

dv/v = dz

∫(dz/z) = ∫(dx/x)

log|z| = log|x| + log|c|

z = xc

log|v| = xc

log|y/x| = xc  (Where ‘c’ is integration constant)

问题19(dy / dx)=(y / x)+ sin(y / x)

解决方案：

We have,

(dy/dx) = (y/x) + sin(y/x)

It is a homogeneous equation,

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = v + sin(v)

x(dv/dx) = sin(v)

dv/sin(v) = (dx/x)

On integrating both sides,

∫dv/sin(v) = ∫(dx/x)

∫cosec(v)dv = ∫(dx/x)

log|tan(v/2)| = log(x) + log(c)

log|tan(y/2x)| = log|xc|

tan(y/2x) = |xc|  (Where ‘c’ is integration constant)

问题20. y ² dx +(x ² – xy + y ² )dy = 0

解决方案：

We have,

y²dx + (x² – xy + y²)dy = 0

(dy/dx) = -(y²)/(x² – xy + y²)

It is a homogeneous equation,

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = -(v²x²)/(x² – xvx + v²x²)

v + x(dv/dx) = -(v²)/(1 – v + v²)

y(dv/dx) = [-(v²)/(1 – v + v²)] – v

$x\frac{dv}{dx}=\frac{-v^2-v+v^2-v^3}{1-v+v^2}$

$\frac{1-v+v^2}{-(v+v^3)}dv=\frac{dx}{x}$

$\frac{1-v+v^2}{-v(1+v^2)}dv=\frac{dx}{x}$

$(\frac{1}{1+v^2}-\frac{1}{v})dv=\frac{dx}{x}$

On integrating both sides,

∫dv/(1 + v²) – ∫dv/v = ∫(dx/x)

tan^-1(v) – log(v) = log(x) + log(c)

tan^-1(y/x) – log|y/x| = log(xc)

tan^-1(y/x) = log|(y/x)xc|

tan^-1(y/x) = log|yc|

$e^{tan^{-1}(\frac{y}{x})}=cy$  (Where ‘c’ is integration constant)

问题21. [x√(x ² + y ² )– y ² ] dx + xydy = 0

解决方案：

We have,

[x√(x² + y²) – y²]dx + xydy = 0

dy/dx = -[x√(x² + y²) – y²]/xy

dy/dx = [y² – x√(x² + y²)]/xy

It is a homogeneous equation,

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = [v²x² – x√(x² + v²x²)]/xvx

v + x(dv/dx) = [v² – √(1 + v²)]/v

x(dv/dx) = [v² – √(1 + v²)]/v – v

$x\frac{dv}{dx}=\frac{v^2-\sqrt{1+v^2}-v^2}{v}$

x(dv/dx) = -(√(1 + v²)/v

vdv/√(1 + v²) = -(dx/x)

On integrating both sides,

∫vdv/√(1 + v²) = -∫(dx/x)

(1/2)∫2vdv/√(1 + v²) = -∫(dx/x)

Let, 1 + v² = z

On differentiating both sides,

2vdv = dz

(1/2)∫dz/√z = -∫(dx/x)

√z = -log|x| + log|c|

√(1 + v²) = log|c/x|

√(x² + y²)/x = log|c/x|

√(x² + y²) = xlog|c/x|    (Where ‘c’ is integration constant)

问题22. x(dy / dx)= y – xcos ² (y / x)

解决方案：

We have,

x(dy/dx) = y – xcos²(y/x)

(dy/dx) = y/x – cos²(y/x)

It is a homogeneous equation,

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = v – cos²(v)

x(dv/dx) = -cos²(v)

dv/cos²(v) = -(dx/x)

On integrating both sides,

∫dv/cos²(v) = -∫(dx/x)

∫sec²vdv = -∫(dx/x)

tan(v) = -log|x| + log|c|

tan(y/x) = log|c/x|  (Where ‘c’ is integration constant)

问题23.(y / x)cos(y / x)dx – {(x / y)sin(y / x)+ cos(y / x)} dy = 0

解决方案：

We have,

 (y/x)cos(y/x)dx – {(x/y)sin(y/x) + cos(y/x)}dy = 0

$\frac{\frac{y}{x}cos\frac{y}{x}}{\frac{x}{y}sin\frac{y}{x}+cos\frac{y}{x}}$

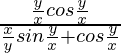
It is a homogeneous equation,

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

$v+x\frac{dv}{dx}=\frac{vcos(v)}{\frac{1}{v}sin(v)+cos(v)}$

$x\frac{dv}{dx}=\frac{v^2cos(v)}{sin(v)+vcos(v)}-v$

x(dv/dx) = (v²cosv – vsinv – v²cosv)/(sinv + vcosv)

x(dv/dx) = -vsinv/(sinv + vcosv)

On integrating both sides,

∫[(sinv + vcosv)/vsinv]dv = -∫(dx/x)

∫(dv/v) + ∫(cotv)dv = -∫(dx/x)

log|v| + log|sinv| = -log|x| + log|c|

log|vsinv| = log|c/x|

(y/x)sin(y/x) = (c/x)

ysin(y/x) = c   (Where ‘c’ is integration constant)

问题24。xylog(x / y)dx + {y ² – x ² log(x / y)} dy = 0

解决方案：

We have,

xylog(x/y)dx + {y² – x²log(x/y)}dy = 0

$\frac{dx}{dy}=\frac{x^2log(\frac{x}{y})-y^2}{xylog(\frac{x}{y})}$

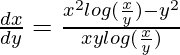
It is a homogeneous equation,

So, put x = vy               (i)

On differentiating both sides w.r.t y,

dx/dy = v + y(dv/dy)

So,

$v+y\frac{dv}{dy}=\frac{v^2y^2log(v)-y^2}{yvylog(v)}$

v + y(dv/dy) = (v²logv – 1)/(vlogv)

y(dv/dy) = [(v²logv – 1)/(vlogv)] – v

y(dv/dy) = (v²logv – 1 – v²logv)/vlogv

y(dv/dy) = -(1/vogv)

vlogvdv = -(dy/y)

On integrating both sides,

∫vlogvdv = -∫(dy/y)

logv∫vdv – ∫{d/dv(logv)∫vdv}dv}dv = -∫(dy/y)

(v²/2)logv – (1/2)∫(1/v)(v²/2)dv = -logy + logc

(v²/2)logv – (1/2)∫vdv = -logy + logc

(v²/2)logv – (v²/4) + logy = log|c|

(v²/2)[logv – 1/2] + logy = log|c|

v²[logv – (1/2)] + logy = log|c|

(x²/y²)[log(x/y) – (1/2)] + logy = log|c|  (Where ‘c’ is integration constant)

问题25。(1 + e ^{x / y} )dx + e ^{x / y} (1 – x / y)dy = 0

解决方案：

We have,

(1 + e^x/y)dx + e^x/y(1 – x/y)dy = 0

$\frac{dx}{dy}=-\frac{e^\frac{x}{y}(1-\frac{x}{y})}{1+e^\frac{x}{y}}$

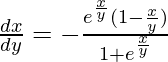
It is a homogeneous equation,

So, put x = vy               (i)

On differentiating both sides w.r.t y,

dx/dy = v + y(dv/dy)

So,

$v+y\frac{dv}{dy}=-\frac{e^v(1-v)}{1+e^v}$

y(dv/dy) = -[e^v(1 – v)/(1 + e^v)] – v

y(dv/dy) = (-e^v + ve^v – v – ve^v)/(1 + e^v)

y(dv/dy) = -(v + ve^v)/(1 + e^v)

[(1 + e^v)/(v + e^v)]dv = -(dy/y)

On integrating both sides,

∫[(1 + e^v)/(v + e^v)]dv = -∫(dy/y)

log|(v + e^v)| = -log(y) + log(c)

log|(v + e^v)| = log|c/y|

(x/y) + e^x/y = c/y

x + ye^x/y = c  (Where ‘c’ is integration constant)

问题26.(x ² + y ² )dy / dx =(8x ² – 3xy + 2y ² )

解决方案：

We have,

(x² + y²)dy/dx = (8x² – 3xy + 2y²)

(dy/dx) = (8x² – 3xy + 2y²)/(x² + y²)

It is a homogeneous equation,  

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = (8x² – 3xvx + 2v²x²)/(x² + v²x²)

v + x(dv/dx) = (8 – 3v + 2v²)/(1 + v²)

x(dv/dx) = [(8 – 3v + 2v²)/(1 + v²)] – v

x(dv/dx) = (8 – 4v + 2v² – v³)/(1 + v²)

(1 + v²)dv/(8 – 4v + 2v² – v³) = (dx/x)

On integrating both sides,

$∫\frac{1+v^2}{4(2-v)+v^2(2-v)}dv=∫\frac{dx}{x}$

$∫\frac{1+v^2}{(2-v)(4+v^2)}dv=∫\frac{dx}{x}$

Using partial fraction,

$∫\frac{1+v^2}{(2-v)(4+v^2)}=\frac{Av+B}{4+v^2}+\frac{C}{2-v}$

(1 + v²) = Av(2 – v) + B(2 – v) + C(4 + v²)

(1 + v²) = 2Av – Av² + 2B – Bv + 4C + Cv²

(1 + v²) = (C – A)v² + (2A – B)v + (2B + 4C)

Comparing the co-efficient of both sides,

(C – A) = 1

(2A – B) = 0

(2B + 4C) = 1

Solving above equations,

A = -(3/8)

B = -(3/4)

C = (5/8)

$∫\frac{-\frac{3}{8}v-\frac{3}{4}}{4+v^2}dv+∫\frac{\frac{5}{8}}{2-v}dv=∫\frac{dx}{x}$

$-\frac{3}{8}∫\frac{vdv}{v^2+1}-\frac{3}{4}∫\frac{dv}{v^2+1}+\frac{5}{8}∫\frac{dv}{2-v}=logx+logc$

$-\frac{3}{16}log|v^2+1|-\frac{3}{8}tan^{-1}(\frac{v}{2})-\frac{5}{8}log|2-v|=log|xc|$

$e^{-\frac{3}{8}tan^{-1}(\frac{v}{2})}=c|x(2-v)^\frac{5}{8}(v^2+4)^\frac{3}{16}|$

$e^{-\frac{3}{8}tan^{-1}(\frac{y}{2x})}=c|x(2-\frac{y}{x})^\frac{5}{8}(\frac{y^2}{x^2}+4)^\frac{3}{16}|$

$e^{-\frac{3}{8}tan^{-1}(\frac{y}{2x})}=c|x(2x-y)^\frac{5}{8}(y^2+4x^2)^\frac{3}{16}|$ (Where ‘c’ is integration constant)