第 12 类 RD Sharma 解 – 第 22 章微分方程 – 练习 22.1 |设置 2

确定下列微分方程的阶和阶。还要说明它是线性的还是非线性的（问题 14-26）

问题 14。 $\sqrt{1-y^2}dx+\sqrt{1-x^2}dy=0$

解决方案：

We have,

$\sqrt{1-y^2}dx+\sqrt{1-x^2}dy=0$

$\frac{dy}{dx}+ \sqrt{\frac{1-y^2}{1-x^2}}=0$

Oder of function:

As the highest order of derivative of function is 1 (i.e., dy/dx)

So, the order of the derivative is equal to 1.

Degree of function:

As the power of the highest order derivative of the function is 1 (i.e., power of dy/dx is 1)

So, the degree of function is 1.

Linear or Non-linear:

The given equation is non-linear.

问题 15。 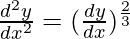$\frac{d^2y}{dx^2}=(\frac{dy}{dx})^\frac{2}{3}$

解决方案：

We have,

$\frac{d^2y}{dx^2}=(\frac{dy}{dx})^\frac{2}{3}$

On cubing both side, we have

$(\frac{d^2y}{dx^2})^3=(\frac{dy}{dx})^2$

Order of function:

The Highest order of derivative of function is 2. (i.e., $\frac{d^2y}{dx^2}$)

So, the order of the derivative is equal to 2.

Degree of function:

As the power of the highest order derivative of the function is 3 (i.e., power of $\frac{d^2y}{dx^2}$ is 3)

So, the degree of function is 3.

Linear or Non-linear:

The given equation is non-linear.

问题 16。 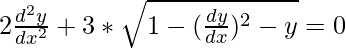$2\frac{d^2y}{dx^2}+3*\sqrt{1-(\frac{dy}{dx})^2-y}=0$

解决方案：

We have,

$2\frac{d^2y}{dx^2}+3*\sqrt{1-(\frac{dy}{dx})^2-y}$

$2\frac{d^2y}{dx^2}=-3*\sqrt{1-(\frac{dy}{dx})^2-y}$

Squaring both sides, we have

$4(\frac{d^2y}{dx^2})^2=9({1-(\frac{dy}{dx})^2-y})$

$4(\frac{d^2y}{dx^2})^2+9(\frac{dy}{dx})^2+9y-9=0$

Order of function:

As the highest order of derivative of function is 2. (i.e., $\frac{d^2y}{dx^2}$)

So, the order of the function is equal to 2.

Degree of function:

As the power of the highest order derivative of the function is 2 (i.e., power of $\frac{d^2y}{dx^2}$ is 2)

So, the Degree of the function is equal to 2.

Linear or Non-linear:

The given equation is non-linear.

问题 17。 $5\frac{d^2y}{dx^2}=[1+(\frac{dy}{dx})^2]^\frac{3}{2}$

解决方案：

We have,

$5\frac{d^2y}{dx^2}=[1+(\frac{dy}{dx})^2]^\frac{3}{2}$

One squaring both side, we have

$[5\frac{d^2y}{dx^2}]^2=[1+(\frac{dy}{dx})^2]^3$

$25(\frac{d^2y}{dx^2})^2=[1+(\frac{dy}{dx})^6+3(\frac{dy}{dx})^2+3(\frac{dy}{dx})^6$

Order of function:

As the highest order of derivative of the function is 2 (i.e., $\frac{d^2y}{dx^2}$)

So, Order of the function is equal to 2.

Degree of function:

As the power of the highest order derivative of the function is 2 (i.e., power of $\frac{d^2y}{dx^2}$ is 2)

So, the Degree of the function is equal to 2.

Linear or Non-linear:

The given equation is non-linear.

问题 18。 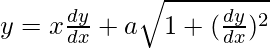$y=x\frac{dy}{dx}+a\sqrt{1+(\frac{dy}{dx})^2}$

解决方案：

We have,

$y=x\frac{dy}{dx}+a\sqrt{1+(\frac{dy}{dx})^2}$

$(y-x\frac{dy}{dx})=-a\sqrt{1+(\frac{dy}{dx})^2}$

On squaring both sides, we get

$(y-x\frac{dy}{dx})^2=a(1+(\frac{dy}{dx})^2$

$x^2(\frac{dy}{dx})^2+y^2-2xy\frac{dy}{dx}=a[1-(\frac{dy}{dx})^2]$

$x^2(\frac{dy}{dx})^2+y^2-2xy\frac{dy}{dx}-a+(\frac{dy}{dx})^2=0$

Order of function:

As the highest order of derivative of the function is 1,

So, the Order of the function is equal to 1.

Degree of function:

As the power of the highest order derivative of the function is 2.(i.e., power of dy/dx is 2)

So, the Degree of the function is equal to 2.

Linear or Non-linear:

The given equation is non-linear.

问题 19。 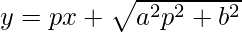$y=px+\sqrt{a^2p^2+b^2}$ , 其中 p = dy/dx

解决方案：

We have

$y=px+\sqrt{a^2p^2+b^2}$, where p = dy/dx 

$(y-px)^2={a^2p^2+b^2}$

$y^2-2pxy+p^2x^2=a^2p^2+b^2$

$(x^2-a^2)(\frac{dy}{dx})^2-2xy(\frac{dy}{dx})+(y^2-b^2)=0$

Order of function:

As the highest order of derivative of function is 1

So, the Order of the function is equal to 1.

Degree of function:

As the power of the highest order derivative of the function is 2 (i.e., power of dy/dx is 2)

So, the Degree of the function is equal to 2.

Linear or Non-linear:

The given equation is non-linear.

问题 20：dy/dx + e ^y = 0

解决方案：

We have,

 dy/dx + e^y = 0 

Order of function:

As the highest order of derivative of the function is 1

So, the Order of the function is equal to 1.

Degree of function:

As the power of the highest order derivative of the function is 1(i.e., power of dy/dx is 1)

So, the Degree of the function is equal to 1.

Linear or Non-linear:

The given equation is non-linear.

问题 21。 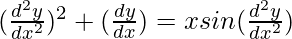$(\frac{d^2y}{dx^2})^2+(\frac{dy}{dx})=xsin(\frac{d^2y}{dx^2})$

解决方案：

We have,

$(\frac{d^2y}{dx^2})^2+(\frac{dy}{dx})=xsin(\frac{d^2y}{dx^2})$

Order of function:

As the highest order of derivative of the function is 2

So, the order of the derivative is equal to 2.

Degree of function:

$sin(\frac{d^2y}{dx^2})$ is not a polynomial function. So degree can not be defined. 

So, the degree of function is not defined.

Linear or Non-linear:

The given equation is non-linear.

问题 22. (y”) ² + (y') ³ + siny = 0

解决方案：

We have,

(y”)² + (y’)³ + siny = 0

Where

 $y''=\frac{d^2y}{dx^2}$

Order of function:

The highest order of derivative of the function is 2. (i.e., y”)

So, the order of the derivative is equal to 2.

Degree of function

As the power of the highest order derivative of the function is 2 (i.e., power of y” is 2)

So, the degree of function is 2.

Linear or Non-linear:

The given equation is non-linear.

问题 23。 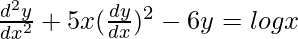$\frac{d^2y}{dx^2}+5x(\frac{dy}{dx})^2-6y=logx$

解决方案：

We have,

$\frac{d^2y}{dx^2}+5x(\frac{dy}{dx})^2-6y=logx$

Order of function:

As the highest order of derivative of the function is 2. 

So, the order of the function is equal to 2.

Degree of function:

As the power of the highest order derivative of the function is 1 (i.e., power of $\frac{d^2y}{dx^2}$ is 1)

So, the Degree of the function is equal to 1.

Linear or Non-linear:

The given equation is non-linear.

问题 24。 $\frac{d^3y}{dx^3}+\frac{d^2y}{dx^2}+\frac{dy}{dx}+ysiny=0$

解决方案：

We have,

$\frac{d^3y}{dx^3}+\frac{d^2y}{dx^2}+\frac{dy}{dx}+ysiny=0$

Order of function:

As the highest order of derivative of the function is 3 

So, the Order of the function is equal to 3.

Degree of function:

As the power of the highest order derivative of the function is 1 (i.e., power of$\frac{d^3y}{dx^3}$ is 1)

So, the Degree of the function is equal to 1.

Linear or Non-linear:

The given equation is linear.

问题 25。 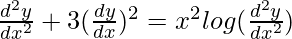$\frac{d^2y}{dx^2}+3(\frac{dy}{dx})^2 =x^2log(\frac{d^2y}{dx^2})$

解决方案：

We have,

$\frac{d^2y}{dx^2}+3(\frac{dy}{dx})^2 =x^2log(\frac{d^2y}{dx^2})$

Order of function:

As the highest order of derivative of the function is 2.

So, the order of the function is equal to 2.

The degree of function:

$log(\frac{d^2y}{dx^2})$ is not a polynomial function. So degree can not be defined. 

So, the degree of function is not defined.

Linear or Non-linear:

The given equation is non-linear.

问题 26。 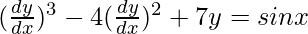$(\frac{dy}{dx})^3-4(\frac{dy}{dx})^2+7y=sinx$

解决方案：

We have,

$(\frac{dy}{dx})^3-4(\frac{dy}{dx})^2+7y=sinx$

$\frac{d^3y}{dx^3}+\frac{d^2y}{dx^2}+\frac{dy}{dx}+ysiny=0$

Order of function:

As the highest order of derivative of the function is 1

So, the Order of the function is equal to 1.

Degree of function:

As the power of the highest order derivative of the function is 3(i.e., power of dy/dx is 3)

So, the Degree of the function is equal to 3.

Linear or Non-linear:

The given equation is non-linear.