第12类RD Sharma解–第22章微分方程–练习22.9 |套装1

解决以下微分方程：

问题1. x ² dy + y(x + y)dy = 0

解决方案：

We have,

x²dy + y(x + y)dy = 0

dy/dx = -y(x + y)/x² 

It is a homogeneous equation, 

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = -vx(x + vx)/x² 

v + x(dv/dx) = -v – v² 

x(dv/dx) = -2v – v² 

$\frac{dv}{(v^2 + 2v)} = -\frac{dx}{x}$

On integrating both sides,

$∫\frac{dv}{(v^2+2v+1-1)}=-∫(\frac{dx}{x})$

$∫\frac{dv}{(v+1)^2-(1)^2}=-log(x)$

$\frac{1}{2}log(\frac{v+1-1}{v+1+1})=-log|x|+log|c|$

log|v/(v + 2)|^1/2 = -log|x/c|

v/(v + 2) = c²/x²

$\frac{\frac{y}{x}}{\frac{y}{x}+2}=\frac{c^2}{x^2}$

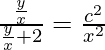
yx² = (y + 2x)c²    (Where ‘c’ is integration constant)

问题2。(dy / dx)=(y – x)/(y + x)

解决方案：

We have,

(dy/dx) = (y – x)/(y + x)

It is a homogeneous equation, 

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = (vx – x)/(vx + x)

v + x(dv/dx) = (v – 1)/(v + 1)

x(dv/dx) = (v – 1)/(v + 1) – v

x(dv/dx) = (v – 1 – v² – v)/(v + 1)

x(dv/dx) = -(v² + 1)/(v + 1)

$\frac{(v+1)dv}{(v^2+1)}=-\frac{dx}{x}$

On integrating both sides,

$∫\frac{(v+1)dv}{(v^2+1)}=-∫\frac{dx}{x}$

∫vdv/(v²+1)+∫dv/(v²+1)=-∫(dx/x)

$\frac{1}{2}∫\frac{2v}{v^2+1}+∫\frac{dv}{v^2+1}=-log|x|+log|c|$

(1/2)log|v² + 1| + tan^-1(v) = log(c/x)

log|(y² + x²)/x²| + 2tan^-1(y/x) = log(c/x)² 

log(y² + x²) – log(x)² + 2tan^-1(y/x) = log(c/x)² 

log(y² + x²) + 2tan^-1(y/x) = 2log(c)  (Where ‘c’ is integration constant)

问题3.(dy / dx)=(y ² – x ² )/ 2yx

解决方案：

We have,

(dy/dx) = (y² – x²)/2yx

It is a homogeneous equation,

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = (v²x² – x²)/2vx²

v + x(dv/dx) = (v² – 1)/2v

x(dv/dx) = [(v² – 1)/2v] – v

x(dv/dx) = (v² – 1 – 2v²)/2v

x(dv/dx) = -(v² + 1)/2v

$\frac{2vdv}{(v^2 + 1)} = -\frac{dx}{x}$

On integrating both sides,

$∫\frac{vdv}{(v^2+1)}=-∫\frac{dx}{x}$

log|v²+1| = -log(x) + log(c)

log|v²+1| = log(c/x)

y²/x² + 1 = |c/x|

(x² + y²) = cx  (Where ‘c’ is integration constant)

问题4. x(dy / dx)=(x + y)

解决方案：

We have,

x(dy/dx) = (x+y)

(dy/dx) = (x+y)/x

It is a homogeneous equation,

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = (x + vx)/x

v + x(dv/dx) = (1 + v)

x(dv/dx) = 1

dv = (dx/x)

On integrating both sides,

∫dv = ∫(dx/x)

v = log(x) + c

y/x = log(x) + c

y = xlog(x) + cx  (Where ‘c’ is integration constant)

问题5.(x ² – y ² )dx – 2xydy = 0

解决方案：

We have,

(x² – y²)dx – 2xydy = 0

(dy/dx) = (x² – y²)/2xy

It is a homogeneous equation,

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = (x² – v²x²)/2xvx

v + x(dv/dx) = (1 – v²)/2v

x(dv/dx) = [(1 – v²)/2v] – v

x(dv/dx) = (1 – 3v²)/2v

$\frac{2vdv}{(1-3v^2)} = \frac{dx}{x}$

On integrating both sides,

$∫\frac{2vdv}{(1-3v^2)}=∫\frac{dx}{x}$

$\frac{1}{3}∫\frac{6v}{1-3v^2}dv=∫\frac{dx}{x}$

-(1/3)log(1 – 3v²) = log(x) – log(c)

log(1 – 3v²) = -log(x)³ + log(c)

$(1-\frac{3y^2}{x^2})=(\frac{c}{x^3})$

(x² – 3y²)/x² = (c/x³)

x(x² – 3y²) = c  (Where ‘c’ is integration constant)

问题6.(dy / dx)=(x + y)/(x – y)

解决方案：

We have,

(dy/dx) = (x + y)/(x – y)

It is a homogeneous equation,  

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = (x + vx)/(x – vx)

v + x(dv/dx) = (1 + v)/(1 – v)

x(dv/dx) = [(1 + v)/(1 – v)] – v

x(dv/dx) = (1 + v – v + v²)/(1 – v)

x(dv/dx) = (1 + v²)/(1 – v)

$\frac{(1-v)dv}{(v^2+1)}=\frac{dx}{x}$

On integrating both sides,

$∫\frac{(v+1)dv}{(v^2+1)}=∫\frac{dx}{x}$

∫dv/(v² + 1) – ∫vdv/(v² + 1) = ∫(dx/x)

tan^-1(v) – (1/2)log(v² + 1) = log(x) + c

tan^-1(y/x) – (1/2)log(y²/x² + 1) = log(x) + c

tan^-1(y/x) – (1/2)log(y² + x²) + log(x) = log(x) + c

tan^-1(y/x) = (1/2)log(y² + x²) + c  (Where ‘c’ is integration constant)

问题7. 2xy(dy / dx)=(x ² + y ² )

解决方案：

We have,

2xy(dy/dx) = (x² + y²)

(dy/dx) = (x² + y²)/2xy

It is a homogeneous equation,

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = (x² + v²x²)/2xvx

v + x(dv/dx) = (1 + v²)/2v

x(dv/dx) = [(1 + v²)/2v] – v

x(dv/dx) = (1 – v²)/2v

$\frac{2vdv}{(1 - v^2)} = \frac{dx}{x}$

On integrating both sides,

$∫\frac{2vdv}{(1 - v^2)} = ∫\frac{dx}{x}$

-log(1 – v²) = log(x) – log(c)

log(1 – v²) = -log(x) + log(c)

1 – y²/x² = (c/x)

(x² – y²) = cx  (Where ‘c’ is integration constant)

问题8. x ² (dy / dx)= x ² – 2y ² + xy

解决方案：

We have,

x²(dy/dx) = x² – 2y² + xy

(dy/dx) = (x² – 2y² + xy)/x²

It is a homogeneous equation,

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = (x² – 2v²x² + xvx)/2xvx

v + x(dv/dx) = (1 – 2v² + v)/x²

x(dv/dx) = (1 – 2v² + v) – v

x(dv/dx) = (1 – 2v²)

dv/(1 – 2v²) = (dx/x)

On integrating both sides,

dv/(1 – 2v²) = ∫(dx/x)

$∫\frac{dv}{v^2-\frac{1}{2}}=-2\frac{dx}{x}$

$∫\frac{dv}{(\frac{1}{\sqrt2})^2-v^2}=2\frac{dx}{x}$

$\frac{1}{\sqrt{2}}log|\frac{\frac{1}{\sqrt{2}}+v}{\frac{1}{\sqrt{2}}-v}|=2log(x)+log(c)$

$\frac{1}{\sqrt{2}}log|\frac{\frac{1}{\sqrt{2}}+\frac{y}{x}}{\frac{1}{\sqrt{2}}-\frac{y}{x}}|=2log(x)+log(c)$

$(\frac{1}{√2})log|\frac{(x + y√2)}{(x - y√2)}|=log(x)^2 + log(c)$

$|\frac{(x + y√2)}{(x - y√2)}|^{\frac{1}{√2}} = cx^2$

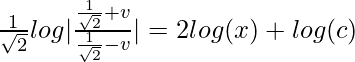
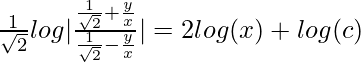
$|\frac{(x+y√2)}{(x-y√2)}|=|cx^2|^{√2}$  (Where ‘c’ is integration constant)

问题9. xy(dy / dx)= x ² – y ²

解决方案：

We have,

xy(dy/dx) = x² – y²

(dy/dx) = (x² – y²)/xy

It is a homogeneous equation,

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = (x² – v²x²)/xvx

v + x(dv/dx) = (1 – v²)/v

x(dv/dx) = [(1 – v²)/v] – v

x(dv/dx) = (1 – 2v²)/v

vdv/(1 – 2v²) = (dx/x)

On integrating both sides,

∫vdv/(1 – 2v²) = ∫(dx/x)

∫4vdv/(1 – 2v²) = 4∫(dx/x)

-log(1 – 2v²) = 4log(x) – log(c)

log(1 – 2v²) = log(c/x⁴)

(1 – 2y²/x²) = c/x⁴

(x²-2y²)/x² = c/x⁴

x²(x² – 2y²) = c  (Where ‘c’ is integration constant)

问题10. ^{y x / y} dx =(xe ^{x / y} + y)dy

解决方案：

We have,

ye^x/ydx = (xe^x/y + y)dy

(dy/dx) = (xe^x/y + y)/ye^x/y

It is a homogeneous equation,

So, put x = vy               (i)

On differentiating both sides w.r.t x,

dx/dy = v + y(dv/dy)

So,

v + y(dv/dy) = (vye^vy/y + y)/ye^vy/y

v + y(dv/dy) = (ve^v + 1)/e^v

y(dv/dy) = [(ve^v + 1)/e^v] – v

y(dv/dy) = (ve^v + 1 – ve^v)/e^v

y(dv/dy) = (1/e^v)

e^vdv = (dy/y)

On integrating both sides,

∫e^vdv = ∫(dy/y)

e^v = log(y) + log(c)

e^x/y = log(y) + log(c)  (Where ‘c’ is integration constant)

问题11.x ² (dy / dx)= x ² + xy + y ²

解决方案：

We have,

x²(dy/dx) = x² + xy + y²

dy/dx = (x² + xy + y²)/x²

It is a homogeneous equation,

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = (x² + xvx + v²x²)/x²

v + x(dv/dx) = (1 + v + v²)

x(dv/dx) = (1 + v + v²) – v

dv/(1 + v²) = (dx/x)

On integrating both sides,

∫dv/(1 + v²) = ∫(dx/x)

tan^-1(v) = log|x| + c

tan^-1(y/x) = log|x| + c    (Where ‘c’ is integration constant)

问题12.(y ² – 2xy)dx =(x ² – 2xy)dy

解决方案：

We have,

(y² – 2xy)dx = (x² – 2xy)dy

(dy/dx) = (y² – 2xy)/(x² – 2xy)

It is a homogeneous equation,

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = (v²x² – 2xvx)/(x² – 2xvx)

v + x(dv/dx) = (v² – 2v)/(1 – 2v)

x(dv/dx) = [(v² – 2v – v + 2v²)/(1 – 2v)]

x(dv/dx) = 3(v² – 1)/(1 – 2v)

-(2v – 1)dv/(v² – v) = 3(dx/x)

On integrating both sides,

-∫(2v – 1)dv/(v² – v) = 3∫(dx/x)

-log|v² – v| = 3log|x| – log|c|

log|v² – v| = log|c/x³|

(y²/x² – y/x) = (c/x³)

(y² – xy) = c/x

x(y² – xy) = c (Where ‘c’ is integration constant)

问题13. 2xydx +(x ² + 2y ² )dy = 0

解决方案：

We have,

2xydx + (x² + 2y²)dy = 0

dy/dx = -(2xy)/(x² + 2y²)

It is a homogeneous equation,

So, put y = vx               (i)

On differentiating both sides w.r.t x,

dy/dx = v + x(dv/dx)

So,

v + x(dv/dx) = -(2xvx)/(x² + 2v²x²)

v + x(dv/dx) = -(2v)/(1 + 2v²)

x(dv/dx) = -[(2v)/(1 + 2v²)] – v

$x\frac{dv}{dx}=\frac{-3v-2v^3}{1+2v^2}$

$\frac{1+2v^2}{3v+2v^3}dv=-\frac{dx}{x}$

On integrating both sides,

$∫\frac{1+2v^2}{3v+2v^3}dv=-∫\frac{dx}{x}$

Substituting (3v + 2v³) = z

On differentiating both sides w.r.t x,

3(1 + 2v)dv = dz

(1 + 2v)dv = (dz/3)

(1/3)∫(dz/z) = -∫(dx/x)

(1/3)log|z| = -log|x| + log|c|

log|3v + 2v³| = log|c/x|³

3y/x + 2(y/x)³ = (c/x)³

(3yx² + 2y³) = c (Where ‘c’ is integration constant)