第12类RD Sharma解决方案–第16章切线和法线–练习16.3

问题1.找到以下曲线的相交角：

(i)y ² = x和x ² = y

解决方案：

First curve is y² = x. . . . . (1)

Differentiating both sides with respect to x, we get,

=> 2y (dy/dx) = 1

=> m₁ = dy/dx = 1/2y

Second curve is x² = y . . . . (2)

Differentiating both sides with respect to x, we get,

=> 2x = dy/dx

=> m₂ = dy/dx = 2x

Solving (1) and (2), we get,

=> x⁴ − x = 0

=> x (x³ − 1) = 0

=> x = 0 or x = 1

We know that the angle of intersection of two curves is given by,

tan θ =$|\frac{m_1-m_2}{1+m_1m_2}|$

where m₁ and m₂ are the slopes of the curves.

When x = 0, then y = 0.

So, m₁ = 1/2y = 1/0 = ∞

m₂ = 2x = 2(0) = 0

Therefore, tan θ =$|\frac{(∞−0)}{1+ 0×∞}|$= ∞

=> θ = π/2

When x = 1, then y = 1.

So, m₁ = 1/2y = 1/2

m₂ = 2x = 2(1) = 2

Therefore, tan θ =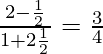$\frac{2-\frac{1}{2}}{1+2×\frac{1}{2}} = \frac{3}{4}$

=> θ = tan⁻¹ (3/4)

(ii)y = x ²和x ² + y ² = 20

解决方案：

First curve is y = x². . . . . (1)

Differentiating both sides with respect to x, we get,

=> (dy/dx) = 2x

=> m₁ = dy/dx = 2x

Second curve is x² + y² = 20 . . . . (2)

Differentiating both sides with respect to x, we get,

=> 2x + 2y (dy/dx) = 0

=> m₂ = dy/dx = −x/y

Solving (1) and (2), we get,

=> y² +y − 20 = 0

=> y² + 5y − 4y − 20 = 0

=> (y + 5) (y − 4) = 0

=> y = −5 or y = 4

Ignoring y = − 5 as x becomes √(−5) in that case, which is not possible.

When y = 4, we get x² = 4

=> x = ±2

We know that the angle of intersection of two curves is given by,

tan θ =$|\frac{m_1-m_2}{1+m_1m_2}|$

where m₁ and m₂ are the slopes of the curves.

When x = ±2 and y = 4, we get,

m₁ = 2x = 2(2) = 4 or ±4

m₂ = −x/y = −2/4 = −1/2

So, tan θ =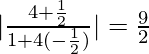$|\frac{4+\frac{1}{2}}{1+4×(-\frac{1}{2})}| = \frac{9}{2}$

=> θ = tan⁻¹ (9/2)

When x = −2 and y = 4, we get,

m₁ = 2x = 4 or −4

m₂ = −x/y = 1/2 or −1/2

So, tan θ =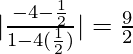$|\frac{-4-\frac{1}{2}}{1-4×(\frac{1}{2})}| = \frac{9}{2}$

=> θ = tan⁻¹ (9/2)

(iii)2y ² = x ³和y ² = 32x

解决方案：

First curve is 2y² = x³. . . . . (1)

Differentiating both sides with respect to x, we get,

=> 4y (dy/dx) = 3x²

=> m₁ = dy/dx = 3x²/4y

Second curve is y² = 32x. . . . . (2)

Differentiating both sides with respect to x, we get,

=> 2y (dy/dx) = 32

=> m₂ = dy/dx = 32/2y = 16/y

Solving (1) and (2), we get,

=> 2(32x) = x³

=> x³ − 64x = 0

=> x(x² − 64) = 0

=> x = 0 or x² − 64 = 0

=> x = 0 or x = ±8

We know that the angle of intersection of two curves is given by,

tan θ =$|\frac{m_1-m_2}{1+m_1m_2}|$

where m₁ and m₂ are the slopes of the curves.

When x = 0 then y = 0.

m₁ = 3x²/4y = ∞

m₂ = 16/y = ∞

So, tan θ = ∞

=> θ = π/2

When x = ±8, then y = ±16.

m₁ = 3x²/4y = 3 or −3

m₂ = 16/y = 1 or −1

So, tan θ =$|\frac{3-1}{1+3×1}| = \frac{1}{2}$

=> θ = tan⁻¹ (1/2)

(iv)x ² + y ² – 4x – 1 = 0和x ² + y ² – 2y – 9 = 0

解决方案：

First curve is x² + y² – 4x – 1 = 0. . . . . (1)

Differentiating both sides with respect to x, we get,

=> 2x + 2y (dy/dx) – 4 = 0

=> m₁ = dy/dx = (2–x)/y

Second curve is x² + y² – 2y – 9 = 0. . . . . (2)

Differentiating both sides with respect to x, we get,

=> 2x + 2y (dy/dx) – 2 (dy/dx) = 0

=> m₂ = dy/dx = –x/(y–1)

First curve can be written as,

=> (x – 2)² + y² – 5 = 0 . . . . (3)

Subtracting (2) from (1), we get

=> x² + y² – 4x – 1 – x² – y² + 2y + 9 = 0

=> – 4x – 1 + 2y + 9 = 0

=> 2y = 4x – 8

=> y = 2x – 4

Putting y = 2x – 4 in (1), we get,

=> (x – 2)² + (2x – 4)² – 5 = 0

⇒ (x – 2)²(1 + 4) – 5 = 0

⇒ 5(x – 2)² – 5 = 0

⇒ (x – 2)² = 1

⇒ x = 3 or x = 1

So, when x = 3 then y = 6 – 4 = 2

m₁ = (2–x)/y = (2–3)/2 = –1/2

m₂ = –x/(y–1) = –3/(2–1) = –3

So, tan θ =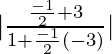$|\frac{\frac{-1}{2}+3}{1+\frac{-1}{2}×(-3)}|$= 1

=> θ = π/4

So, when x = 1 then y = 2 – 4 = – 2

m₁ = (2–x)/y = (2–1)/(–2) = –1/2

m₂ = –x/(y–1) = –1/(–2–1) = 1/3

So, tan θ =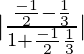$|\frac{\frac{-1}{2}-\frac{1}{3}}{1+\frac{-1}{2}×\frac{1}{3}}|$= 1

=> θ = π/4

(v)x ² / a ² + y ² / b ² = 1和x ² + y ² = ab

解决方案：

First curve is x²/a² + y²/b² = 1 . . . . (1)

Differentiating both sides with respect to x, we get,

=> 2x/a² + (2y/b²) (dy/dx) = 0

=> m₁ = dy/dx = –b²x/a²y

Second curve is x² + y² = ab . . . . (2)

Differentiating both sides with respect to x, we get,

=> 2x + 2y (dy/dx) = 0

=> m₂ = dy/dx = –2x/2y = –x/y

Solving (1) and (2), we get,

=> x²/a² + (ab – x²)/b² = 1

=> x²b² – a²x² = a²b² – a³b

=> x² =$\frac{a^2b(b-a)}{b^2-a^2}$

=> x =$\pm\sqrt{\frac{a^2b}{a+b}}$

From (2), we get, y² =$ab-\frac{a^2b}{a+b}$

=> y =$\pm\sqrt{\frac{ab^2}{a+b}}$

So, m₁ = –b²x/a²y =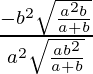$\frac{-b^2\sqrt{\frac{a^2b}{a+b}}}{a^2\sqrt{\frac{ab^2}{a+b}}}$

=$\frac{-b\sqrt{b}}{a\sqrt{a}}$

m₂ = –x/y =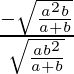$\frac{-\sqrt{\frac{a^2b}{a+b}}}{\sqrt{\frac{ab^2}{a+b}}}$

=$\frac{-\sqrt{a}}{\sqrt{b}}$

Therefore, tan θ =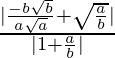$\frac{|\frac{-b\sqrt{b}}{a\sqrt{a}}+\sqrt{\frac{a}{b}}|}{|1+\frac{a}{b}|}$

=> tan θ =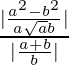$\frac{|\frac{a^2-b^2}{a\sqrt{a}b}|}{|\frac{a+b}{b}|}$

=> tan θ =$\frac{a-b}{\sqrt{a}b}$

=> θ = tan^–1 ((a–b)/√ab)

(vi)x ² + 4y ² = 8和x ² – 2y ² = 2

解决方案：

First curve is x² + 4y² = 8 . . . . (1)

Differentiating both sides with respect to x, we get,

=> 2x + 8y (dy/dx) = 0

=> m₁ = dy/dx = –2x/8y = –x/4y

Second curve is x² – 2y² = 2 . . . . (2)

Differentiating both sides with respect to x, we get,

=> 2x – 4y (dy/dx) = 0

=> m₂ = dy/dx = x/2y

Solving (1) and (2), we get,

6y² = 6 => y2 = ±1

x² = 2 + 2 => x = ±2

So, tan θ =$|\frac{1-2}{1+1×2}|=\frac{1}{3}$

=> θ = tan^–1 (1/3)

(vii)x ² = 27y和y ² = 8x

解决方案：

First curve is x² = 27y . . . . (1)

Differentiating both sides with respect to x, we get,

=> 2x = 27 (dy/dx)

=> m₁ = dy/dx = 2x/27

Second curve is y² = 8x . . . . (2)

Differentiating both sides with respect to x, we get,

=> 2y (dy/dx) = 8

=> m₂ = dy/dx = 8/2y = 4/y

Solving (1) and (2), we get,

=> y⁴/64 = 27y

=> y (y³ − 1728) = 0

=> y = 0 or y = 12

And x = 0 or x = 18.

So, when x = 0 and y = 0

m₁ = 0 and m₂ = ∞

tan θ =$|\frac{0-∞}{1+0×∞}|$= ∞

=> θ = π/2

So, when x = 18 and y = 12

m₁ = 2x/27 = 12/9 = 4/3 and m₂ = 4/y = 1/3

tan θ =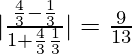$|\frac{\frac{4}{3}-\frac{1}{3}}{1+\frac{4}{3}×\frac{1}{3}}|=\frac{9}{13}$

=> θ = tan⁻¹ (9/13)

(viii)x ² + y ² = 2x和y ² = x

解决方案：

First curve is x² + y² = 2x . . . . (1)

Differentiating both sides with respect to x, we get,

=> 2x + 2y (dy/dx) = 2

=> m₁ = dy/dx = (1–x)/y

Second curve is y² = x . . . . (2)

Differentiating both sides with respect to x, we get,

=> 2y (dy/dx) = 1

=> m₂ = dy/dx = 1/2y

Solving (1) and (2), we get,

=> x² – x = 0

=> x = 0 or x = 1

And y = 0 or y = ±1.

When x = 0, y = 0, m₁ = ∞ and m₂ = ∞

tan θ =$|\frac{∞-∞}{1+∞×∞}| = ∞$

=> θ = π/2

When x = 1 and y = ±1, m₁ = 0 and m₂ = 1/2

tan θ =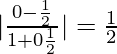$|\frac{0-\frac{1}{2}}{1+0×\frac{1}{2}}|=\frac{1}{2}$

=> θ = tan⁻¹ (1/2)

(ix)y = 4 − x ²和y = x ²

解决方案：

First curve is y = 4 − x² . . . . (1)

Differentiating both sides with respect to x, we get,

=> dy/dx = −2x

=> m₁ = dy/dx = −2x

Second curve is y = x² . . . . (2)

Differentiating both sides with respect to x, we get,

=> dy/dx = 2x

=> m₂ = dy/dx = 2x

Solving (1) and (2), we get,

=> 2x² = 4

=> x = ±√2

And y = 2

So, m₁ = −2x = −2√2 and m₂ = 2x = 2√2

tan θ =$|\frac{-2\sqrt{2}-2\sqrt{2}}{1+(-2\sqrt{2})×2\sqrt{2}}|=\frac{4\sqrt{2}}{7}$

=> θ = tan⁻¹ (4√2/7)

问题2。证明以下曲线组正交相交：

(i)y = x ³和6y = 7 – x ²

解决方案：

First curve is y = x³ . . . . (1)

Differentiating both sides with respect to x, we get,

=> dy/dx = 3x²

=> m₁ = dy/dx = 3x²

Second curve is 6y = 7 – x² . . . . (2)

Differentiating both sides with respect to x, we get,

=> 6y (dy/dx) = – 2x

=> m₂ = dy/dx = –2x/6y = – x/3y

Solving (1) and (2), we get,

=> 6y = 7 – x²

=> 6x³ + x² – 7 = 0

As x = 1 satisfies this equation, we get x = 1 and y = 1³ = 1

So, m₁ = 3 and m₂ = – 1/3

Two curves intersect orthogonally if m₁m₂ = –1

=> 3 × (–1/3) = –1

Hence proved.

(ii)x ³ – 3xy ² = – 2和3x ² y – y ³ = 2

解决方案：

First curve is x³ – 3xy² = – 2

Differentiating both sides with respect to x, we get,

=> 3x² – 3y² – 6xy (dy/dx) = 0

=> m₁ = dy/dx = 3(x²–y²)/6xy

Second curve is 3x²y – y³ = 2

Differentiating both sides with respect to x, we get,

=> 6xy + 3x² (dy/dx) – 3y² (dy/dx) = 0

=> m₂ = dy/dx = –6xy/3(x²–y²)

Two curves intersect orthogonally if m₁m₂ = –1

=>$\frac{3(x^2-y^2)}{6xy}×\frac{-6xy}{3(x^2-y^2)}$= –1

Hence proved.

(iii)x ² + 4y ² = 8和x ² – 2y ² = 4

解决方案：

First curve is x² + 4y² = 8 . . . . (1)

Differentiating both sides with respect to x, we get,

=> 2x + 8y (dy/dx) = 0

=> m₁ = dy/dx = 2x/8y = –x/4y

Second curve is x² – 2y² = 4 . . . . (2)

Differentiating both sides with respect to x, we get,

=> 2x – 4y (dy/dx) = 0

=> m₂ = dy/dx = 2x/4y = x/2y

Solving (1) and (2), we get,

=> x = 4/√3 and y = √2/√3

So, m₁ = –x/4y = –1/√2

m₂ = x/2y = √2

Two curves intersect orthogonally if m₁m₂ = –1

=> (–1/√2) × √2 = –1

Hence proved.

问题3.显示曲线：

(i)x ² = 4y和4y + x ² = 8在(2，1)处正交。

解决方案：

First curve is x² = 4y

Differentiating both sides with respect to x, we get,

=> 2x = 4 (dy/dx)

=> m₁ = dy/dx = 2x/4 = x/2

Second curve is 4y + x² = 8

Differentiating both sides with respect to x, we get,

=> 4 (dy/dx) + 2x = 0

=> m₂ = dy/dx = −2x/4 =−x/2

For x = 2 and y = 1, we have m₁ = 2/2 = 1 and m₂ = −x/2 = −1.

Two curves intersect orthogonally if m₁m₂ = –1

=> 1 × (–1) = –1

Therefore these two curves intersect orthogonally at (2, 1).

Hence proved.

(ii)x ² = y和x ³ + 6y = 7在(1，1)处正交相交。

解决方案：

First curve is x² = y

Differentiating both sides with respect to x, we get,

=> 2x = dy/dx

=> m₁ = dy/dx = 2x

Second curve is x³ + 6y = 7

Differentiating both sides with respect to x, we get,

=> 3x² + 6 (dy/dx) = 0

=> m₂ = dy/dx = −3x²/6 =−x²/2

For x = 1 and y = 1, we have m₁ = 2(1) = 2 and m₂ = −(1)²/2 = −1/2.

Two curves intersect orthogonally if m₁m₂ = –1

=> 2 × (–1/2) = –1

Therefore these two curves intersect orthogonally at (1, 1).

Hence proved.

(iii)y ² = 8x和2x ² + y ² = 10在(1，2√2)处正交相交。

解决方案：

First curve is y² = 8x

Differentiating both sides with respect to x, we get,

=> 2y (dy/dx) = 8

=> m₁ = dy/dx = 8/2y = 4/y

Second curve is 2x² + y² = 10

Differentiating both sides with respect to x, we get,

=> 4x + 2y (dy/dx) = 0

=> m₂ = dy/dx = −4x/2y =−2x/y

For x = 1 and y = 2√2, we have m₁ = 4/2√2 = √2 and m₂ = −2/2√2 = −1/√2

Two curves intersect orthogonally if m₁m₂ = –1

=> √2 × (−1/√2) = –1

Therefore these two curves intersect orthogonally at (1, 2√2).

Hence proved.

^{问题4：如果k 2} = 512，则曲线4x = y ²和4xy = k切成直角。

解决方案：

First curve is 4x = y² . . . . (1)

Differentiating both sides with respect to x, we get,

=> 2y (dy/dx) = 4

=> m₁ = dy/dx = 4/2y = 2/y

Second curve is 4xy = k . . . . (2)

Differentiating both sides with respect to x, we get,

=> y + x (dy/dx) = 0

=> m₂ = dy/dx = −y/x

Solving (1) and (2), we get,

=> y³ = k

=> y = k^1/3

So, x = k^2/3/4

As the curves intersect cut at right angles so, m₁m₂ = –1

=> (2/y) × (−y/x) = –1

=> 2/x = 1

=> 8/k^2/3 = 1

=> k^2/3 = 8

=> k² = 512

Hence proved.

^{问题5。证明如果k 2} = 8，则曲线2x = y ²和2xy = k切成直角。

解决方案：

First curve is 2x = y² . . . . (1)

Differentiating both sides with respect to x, we get,

=> 2y (dy/dx) = 2

=> m₁ = dy/dx = 2/2y = 1/y

Second curve is 2xy = k . . . . (2)

Differentiating both sides with respect to x, we get,

=> y + x (dy/dx) = 0

=> m₂ = dy/dx = −y/x

Solving (1) and (2), we get,

=> y³ = k

=> y = k^1/3

So, x = k^2/3/2

As the curves intersect cut at right angles so, m₁m₂ = –1

=> (1/y) × (−y/x) = –1

=> 1/x = 1

=> 2/k^2/3 = 1

=> k^2/3 = 2

=> k² = 8

Hence proved.

问题6.证明曲线xy = 4和x ² + y ² = 8相互接触。

解决方案：

We have,

xy = 4 . . . . (1)

x² + y² = 8 . . . . (2)

Solving (1) and (2), we get,

=> (4/y)² + y² = 8

=> y⁴ − 8y² + 16 = 0

=> (y² − 4)² = 0

=> y = ±2

And we get x = ±2.

Differentiating eq. (1) with respect to x, we get,

=> y + x (dy/dx) = 0

=> m₁ = dy/dx = −y/x

Differentiating eq. (2) with respect to x, we get,

=> 2x + 2y (dy/dx) = 0

=> dy/dx = −x/y

At x = 2 and y = 2, we have,

m₁ = −2/2 = −1 and also m₂ = −2/2 = −1. Therefore m₁ = m₂.

Also at x = −2 and y = −2, we have m₁ = m₂

So, we can say that the curves touch each other at (2, 2) and (−2, −2).

Hence proved.

问题7.证明曲线y ² = 4x和x ² + y ² − 6x + 1 = 0在点(1，2)彼此接触。

解决方案：

We have,

y² = 4x . . . . (1)

Differentiating both sides with respect to x, we get,

=> 2y (dy/dx) = 4

=> m₁ = dy/dx = 2/y

Also we have,

x² + y² − 6x + 1 = 0 . . . . (2)

Differentiating both with respect to x, we get,

=> 2x + 2y (dy/dx) − 6 = 0

=> m₂ = dy/dx = (6−2x)/2y = (3−x)/y

At x = 1 and y = 2, we have,

m₁ = 2/2 = 1

m₂ = (3−1)/2 = 1.

As m₁ = m₂, we can say that the curves touch each other at (1, 2).

Hence proved.

问题8.找到以下曲线正交相交的条件：

(i)x ² / a ² -y ² / b ² = 1和xy = c ²

解决方案：

We have,

x²/a² − y²/b² = 1

Differentiating both sides with respect to x, we get,

=> 2x/a² − (2y/b²) (dy/dx) = 0

=> m₁ = dy/dx = b²x/a²y

Also, xy = c²

Differentiating both sides with respect to x, we get,

=> y + x (dy/dx) = 0

=> m₂ = dy/dx = −y/x

For curves to intersect orthogonally, m₁ m₂ = −1.

=> (b²x/a²y) (−y/x) = −1

=> a² = b²

Therefore, a² = b² is the condition for the curves to intersect orthogonally.

(ii)x ² / a ² + y ² / b ² = 1和x ² / A ² -y ² / B ² = 1

解决方案：

We have,

x²/a² + y²/b² = 1 . . . . (1)

Differentiating both sides with respect to x, we get,

=> 2x/a² + (2y/b²) (dy/dx) = 0

=> m₁ = dy/dx = −b²x/a²y

Also, x²/A² − y²/B² = 1 . . . . (2)

=> 2x/A² − (2y/B²) (dy/dx) = 0

=> m₂ = dy/dx = B²x/A²y

For curves to intersect orthogonally, m₁ m₂ = −1.

=> (−b²x/a²y) (B²x/A²y) = −1

=> x²/y² = a²A²/b²B² . . . . (3)

Subtracting (2) from (1) gives,

=>$x^2[\frac{1}{a^2}-\frac{1}{A^2}]+y^2[\frac{1}{b^2}+\frac{1}{B^2}]=0$

=>$\frac{x^2}{y^2}=(\frac{b^2+B^2}{b^2B^2})×(\frac{a^2-A^2}{a^2A^2})$

Putting this value in (3), we get,

=>$\frac{b^2+B^2}{b^2B^2}×\frac{a^2-A^2}{a^2A^2}=\frac{a^2A^2}{b^2B^2}$

=> B² + b² = a² − A²

=> a² − b² = A² + B²

Therefore, a² − b² = A² + B² is the condition for the curves to intersect orthogonally.

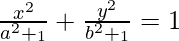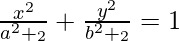问题9.显示曲线$\frac{x^2}{a^2+λ_1}+\frac{y^2}{b^2+λ_1}=1$和$\frac{x^2}{a^2+λ_2}+\frac{y^2}{b^2+λ_2}=1$相交成直角。

解决方案：

We have,

$\frac{x^2}{a^2+λ_1}+\frac{y^2}{b^2+λ_1}=1$. . . . (1)

Differentiating both sides with respect to x, we get,

=> 2x/(a² + λ₁) + 2y/(b² + λ₁) (dy/dx) = 0

=> m₁ = dy/dx =$\frac{−x(b^2 + λ_1)}{y(a^2 + λ_1)}$

Also we have,

$\frac{x^2}{a^2+λ_2}+\frac{y^2}{b^2+λ_2}=1$. . . . (2)

Differentiating both sides with respect to x, we get,

=> 2x/(a² + λ₂) + 2y/(b² + λ₂) (dy/dx) = 0

=> m₂ = dy/dx =$\frac{−x(b^2 + λ_2)}{y(a^2 + λ_2)}$

For curves to intersect orthogonally, m₁ m₂ = −1.

=>$m_1m_2=\frac{−x(b^2 + λ_1)}{y(a^2 + λ_1)}×\frac{−x(b^2 + λ_2)}{y(a^2 + λ_2)}$

=>$m_1m_2=\frac{x^2}{y^2}×\frac{(b^2 + λ_1)(b^2 + λ_2)}{(a^2 + λ_1)(a^2 + λ_2)}$. . . . (3)

Subtracting (2) from (1) gives,

=>$x^2[\frac{1}{a^2+λ_1}-\frac{1}{a^2+λ_2}]+y^2[\frac{1}{b^2+λ_1}-\frac{1}{b^2+λ_2}]=0$

=>$\frac{x^2}{y^2}=\frac{λ_2-λ_1}{(b^2+λ_1)(b^2+λ_2)}×\frac{(a^2+λ_1)(a^2+λ_2)}{λ_1-λ_2}$

Putting this value in (3), we get,

=>$m_1m_2=\frac{λ_2-λ_1}{(b^2+λ_1)(b^2+λ_2)}×\frac{(a^2+λ_1)(a^2+λ_2)}{λ_1-λ_2}×\frac{(b^2 + λ_1)(b^2 + λ_2)}{(a^2 + λ_1)(a^2 + λ_2)}$

=> m₁m₂ = −1

Hence proved.

问题10.如果直线X COSα+ Y罪α= P触及曲线^×2/2 – Y ² / B ² = 1，则证明² COS ^2α – B ²罪^2α= P ² 。

解决方案：

Suppose (x₁, y₁) is the point where the straight line x cos α + y sin α = p touches the curve

x²/a² − y²/b² = 1.

Now equation of tangent to x²/a² − y²/b² = 1 at (x₁, y₁) will be,

=>$\frac{xx_1}{a^2}-\frac{yy_1}{b^2}=1$

Therefore, the equation$\frac{xx_1}{a^2}-\frac{yy_1}{b^2}=1$and the straight line x cos α + y sin α = p represent the same line. So, we get,

=>$\frac{x_1}{a^2cosα}=\frac{-y_1}{b^2sinα}=\frac{1}{p}$

=> x₁ = a² (cos α)/p and x₂ = b² (sin α)/p . . . . (1)

Now the point (x₁, y₁) lies on the curve x²/a² − y²/b² = 1.

=>$\frac{x^2_1}{a^2}−\frac{y^2_1}{b^2}=1$

Using (1), we get,

=>$\frac{a^4cos^2α}{p^2a^2}-(\frac{-b^4sin^2α}{p^2b^2})=1$

=> a² cos²α − b² sin²α = p²

Hence proved.