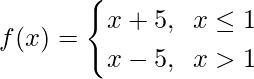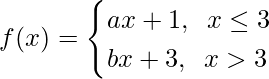问题1.证明函数f(x)= 5x – 3在x = 0,x = – 3和x = 5时是连续的。
解决方案:
To prove the continuity of the function f(x) = 5x – 3, first we have to calculate limits and function value at that point.
Continuity at x = 0
Left limit = ![]()
= (5(0) – 3) = -3
Right limit = ![]()
= (5(0) – 3)= -3
Function value at x = 0, f(0) = 5(0) – 3 = -3
As, ![]() ,
,
Hence, the function is continuous at x = 0.
Continuity at x = -3
Left limit = ![]()
= (5(-3) – 3) = -18
Right limit = ![]()
= (5(-3) – 3) = -18
Function value at x = -3, f(-3) = 5(-3) – 3 = -18
As, ![]()
Hence, the function is continuous at x = -3.
Continuity at x = 5
Left limit = ![]()
= (5(5) – 3) = 22
Right limit = ![]()
= (5(5) – 3) = 22
Function value at x = 5, f(5) = 5(5) – 3 = 22
As, ![]()
Hence, the function is continuous at x = 5.
问题2.检查函数f(x)= 2x 2 – 1在x = 3的连续性。
解决方案:
To prove the continuity of the function f(x) = 2x2 – 1, first we have to calculate limits and function value at that point.
Continuity at x = 3
Left limit = ![]()
= (2(3)2 – 1) = 17
Right limit = ![]()
= (2(3)2 – 1) = 17
Function value at x = 3, f(3) = 2(3)2 – 1 = 17
As, ![]()
Hence, the function is continuous at x = 3.
问题3.检查以下功能的连续性。
(a)f(x)= x – 5
解决方案:
To prove the continuity of the function f(x) = x – 5, first we have to calculate limits and function value at that point.
Let’s take a real number, c
Continuity at x = c
Left limit = ![]()
= (c – 5) = c – 5
Right limit = ![]()
= (c – 5) = c – 5
Function value at x = c, f(c) = c – 5
As, ![]() for any real number c
for any real number c
Hence, the function is continuous at every real number.
(b) 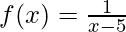 ,x≠5
,x≠5
解决方案:
To prove the continuity of the function f(x) = ![]() , first we have to calculate limits and function value at that point.
, first we have to calculate limits and function value at that point.
Let’s take a real number, c
Continuity at x = c and c ≠ 5
Left limit = 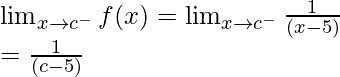
Right limit = 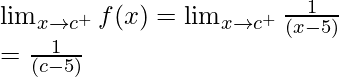
Function value at x = c, f(c) = ![]()
As, ![]() for any real number c
for any real number c
Hence, the function is continuous at every real number.
(C) 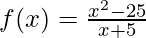 ,x≠-5
,x≠-5
解决方案:
To prove the continuity of the function f(x) = ![]() , first we have to calculate limits and function value at that point.
, first we have to calculate limits and function value at that point.
Let’s take a real number, c
Continuity at x = c and c ≠ -5
Left limit = 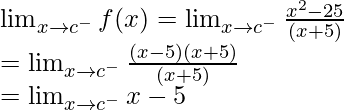
= c – 5
Right limit = 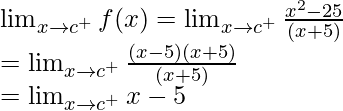
= c – 5
Function value at x = c, f(c) = 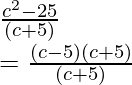
= c – 5
As, ![]() , for any real number c
, for any real number c
Hence, the function is continuous at every real number.
(d)f(x)= | x – 5 |
解决方案:
To prove the continuity of the function f(x) = |x – 5|, first we have to calculate limits and function value at that point.
Here,
As, we know that modulus function works differently.
In |x – 5|, |x – 5| = x – 5 when x>5 and |x – 5| = -(x – 5) when x < 5
Let’s take a real number, c and check for three cases of c:
Continuity at x = c
When c < 5
Left limit = 
= -(c – 5)
= 5 – c
Right limit = 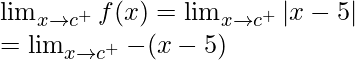
= -(c – 5)
= 5 – c
Function value at x = c, f(c) = |c – 5| = 5 – c
As, ![]()
Hence, the function is continuous at every real number c, where c<5.
When c > 5
Left limit = 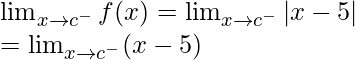
= (c – 5)
Right limit = 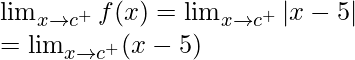
= (c – 5)
Function value at x = c, f(c) = |c – 5| = c – 5
As, ![]() ,
,
Hence, the function is continuous at every real number c, where c > 5.
When c = 5
Left limit = 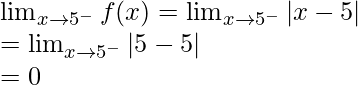
Right limit = 
Function value at x = c, f(c) = |5 – 5| = 0
As, ![]()
Hence, the function is continuous at every real number c, where c = 5.
Hence, we can conclude that, the modulus function is continuous at every real number.
问题4.证明函数f(x)= x n在x = n处是连续的,其中n是一个正整数。
解决方案:
To prove the continuity of the function f(x) = xn, first we have to calculate limits and function value at that point.
Continuity at x = n
Left limit = ![]()
= nn
Right limit = ![]()
= nn
Function value at x = n, f(n) = nn
As, ![]()
Hence, the function is continuous at x = n.
问题5:函数f是否定义为
连续于x = 0?在x = 1时?在x = 2时?
To prove the continuity of the function f(x), first we have to calculate limits and function value at that point.
Continuity at x = 0
Left limit = 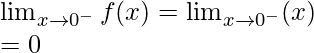
Right limit = 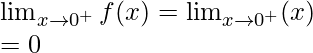
Function value at x = 0, f(0) = 0
As, ![]()
Hence, the function is continuous at x = 0.
Continuity at x = 1
Left limit = 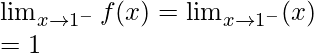
Right limit = 
Function value at x = 1, f(1) = 1
As, ![]() ,
,
Hence, the function is not continuous at x = 1.
Continuity at x = 2
Left limit = 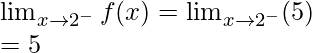
Right limit = 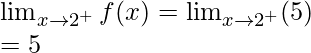
Function value at x = 2, f(2) = 5
As, ![]() ,
,
Therefore, the function is continuous at x = 2.
找出f的所有不连续点,其中f定义为
问题6。 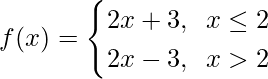
解决方案:
Here, as it is given that
For x ≤ 2, f(x) = 2x + 3, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (-∞, 2)
Now, For x > 2, f(x) = 2x – 3, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (2, ∞)
So now, as f(x) is continuous in x ∈ (-∞, 2) U (2, ∞) = R – {2}
Let’s check the continuity at x = 2,
Left limit = ![]()
= (2(2) + 3)
= 7
Right limit = ![]()
= (2(2) – 3)
= 1
Function value at x = 2, f(2) = 2(3) + 3 = 7
As, ![]()
Therefore, the function is discontinuous at only x = 2.
问题7。 
解决方案:
Here, as it is given that
For x ≤ -3, f(x) = |x| + 3,
As, we know that modulus function works differently.
In |x|, |x – 0| = x when x > 0 and |x – 0| = -x when x < 0
f(x) = -x + 3, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (-∞, -3)
For -3 < x < 3, f(x) = -2x, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (-3, 3)
Now, for x ≥ 3, f(x) = 6x + 2, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (3, ∞)
So now, as f(x) is continuous in x ∈ (-∞, -3) U(-3, 3) U (3, ∞) = R – {-3, 3}
Let’s check the continuity at x = -3,
Left limit = 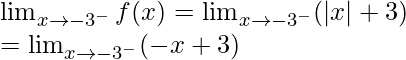
= (-(-3) + 3)
= 6
Right limit = ![]()
= (-2(-3))
= 6
Function value at x = -3, f(-3) = |-3| + 3 = 3 + 3 = 6
As, ![]()
Hence, the function is continuous at x = -3.
Now, let’s check the continuity at x = 3,
Left limit = ![]()
= (-2(3))
= -6
Right limit = ![]()
= (6(3) + 2)
= 20
Function value at x = 3, f(3) = 6(3) + 2 = 20
As, ![]()
Therefore, the function is discontinuous only at x = 3.
问题8。 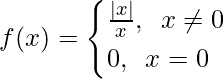
解决方案:
As, we know that modulus function works differently.
In |x|, |x – 0| = x when x > 0 and |x – 0|= -x when x < 0
When x < 0, f(x) = ![]() = -1, which is a constant
= -1, which is a constant
As constant functions are continuous, hence f(x) is continuous x ∈ (-∞, 0).
When x > 0, f(x) = ![]() = 1, which is a constant
= 1, which is a constant
As constant functions are continuous, hence f(x) is continuous x ∈ (0, ∞).
So now, as f(x) is continuous in x ∈ (-∞, 0) U(0, ∞) = R – {0}
Let’s check the continuity at x = 0,
Left limit = 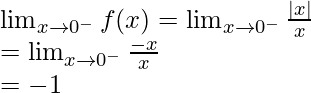
Right limit = 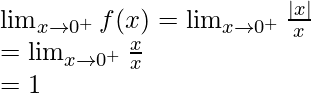
Function value at x = 0, f(0) = 0
As, ![]()
Hence, the function is discontinuous at only x = 0.
问题9。 
解决方案:
As, we know that modulus function works differently.
In |x|, |x – 0| = x when x > 0 and |x – 0| = -x when x < 0
When x < 0, f(x) = ![]() = -1, which is a constant
= -1, which is a constant
As constant functions are continuous, hence f(x) is continuous x ∈ (-∞, 0).
When x > 0, f(x) = -1, which is a constant
As constant functions are continuous, hence f(x) is continuous x ∈ (0, ∞).
So now, as f(x) is continuous in x ∈ (-∞, 0) U(0, ∞) = R – {0}
Let’s check the continuity at x = 0,
Left limit = 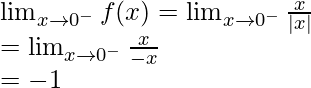
Right limit = 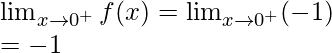
Function value at x = 0, f(0) = -1
As, ![]()
Hence, the function is continuous at x = 0.
So, we conclude that the f(x) is continuous at any real number. Hence, no point of discontinuity.
问题10。 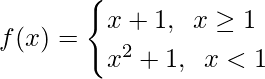
解决方案:
Here,
When x ≥1, f(x) = x + 1, which is a polynomial
As polynomial functions are continuous, hence f(x) is continuous x ∈ (1, ∞)
When x < 1, f(x) = x2 + 1, which is a polynomial
As polynomial functions are continuous, hence f(x) is continuous x ∈ (-∞, 1)
So now, as f(x) is continuous in x ∈ (-∞, 1) U (1, ∞) = R – {1}
Let’s check the continuity at x = 1,
Left limit = ![]()
= 1 + 1
= 2
Right limit = ![]()
= 1 + 1
= 2
Function value at x = 1, f(1) = 1 + 1 = 2
As, ![]()
Hence, the function is continuous at x = 1.
So, we conclude that the f(x) is continuous at any real number.
问题11 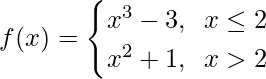
解决方案:
Here,
When x ≤ 2, f(x) = x3 + 3, which is a polynomial
As polynomial functions are continuous, hence f(x) is continuous x ∈ (-∞, 2)
When x > 2, f(x) = x2 + 1, which is a polynomial
As polynomial functions are continuous, hence f(x) is continuous x ∈ (2, ∞)
So now, as f(x) is continuous in x ∈ (-∞, 2) U(2, ∞) = R – {2}
Let’s check the continuity at x = 2,
Left limit = 
Right limit = 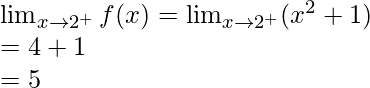
Function value at x = 2, f(2) = 8 – 3 = 5
As, ![]()
Hence, the function is continuous at x = 2.
So, we conclude that the f(x) is continuous at any real number.
问题12。 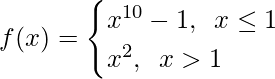
解决方案:
Here,
When x ≤ 1, f(x) = x10 – 1, which is a polynomial
As polynomial functions are continuous, hence f(x) is continuous x ∈ (-∞, 1)
When x >1, f(x) = x2, which is a polynomial
As polynomial functions are continuous, hence f(x) is continuous x ∈ (1, ∞)
So now, as f(x) is continuous in x ∈ (-∞, 1) U (1, ∞) = R – {1}
Let’s check the continuity at x = 1,
Left limit = ![]()
= 1 – 1
= 0
Right limit = 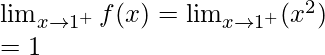
Function value at x = 1, f(1) = 1 – 1 = 0
As, ![]()
Hence, the function is discontinuous at x = 1.
问题13:函数是否由以下项定义
连续函数?
解决方案:
Here, as it is given that
For x ≤ 1, f(x) = x + 5, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (-∞, 1)
Now, For x > 1, f(x) = x – 5, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (1, ∞)
So now, as f(x) is continuous in x ∈ (-∞, 1) U (1, ∞) = R – {1}
Let’s check the continuity at x = 1,
Left limit = ![]()
= (1 + 5)
= 6
Right limit = ![]()
= (1 – 5)
= -4
Function value at x = 1, f(1) = 5 + 1 = 6
As, ![]()
Hence, the function is continuous for only R – {1}.
讨论函数f的连续性,其中f由
问题14。 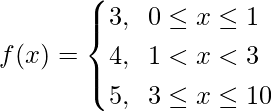
解决方案:
Here, as it is given that
For 0 ≤ x ≤ 1, f(x) = 3, which is a constant
As constants are continuous, hence f(x) is continuous x ∈ (0, 1)
Now, For 1 < x < 3, f(x) = 4, which is a constant
As constants are continuous, hence f(x) is continuous x ∈ (1, 3)
For 3 ≤ x ≤ 10, f(x) = 5, which is a constant
As constants are continuous, hence f(x) is continuous x ∈ (3, 10)
So now, as f(x) is continuous in x ∈ (0, 1) U (1, 3) U (3, 10) = (0, 10) – {1, 3}
Let’s check the continuity at x = 1,
Left limit = 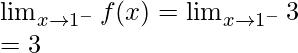
Right limit = 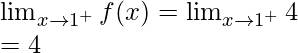
Function value at x = 1, f(1) = 3
As, ![]()
Hence, the function is discontinuous at x = 1.
Now, let’s check the continuity at x = 3,
Left limit = 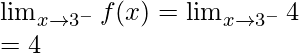
Right limit = 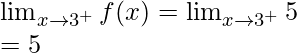
Function value at x = 3, f(3) = 4
As, ![]()
Hence, the function is discontinuous at x = 3.
So concluding the results, we get
Therefore, the function f(x) is discontinuous at x = 1 and x = 3.
问题15。 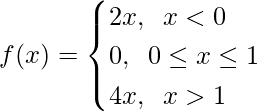
解决方案:
Here, as it is given that
For x < 0, f(x) = 2x, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (-∞, 0)
Now, For 0 ≤ x ≤ 1, f(x) = 0, which is a constant
As constant are continuous, hence f(x) is continuous x ∈ (0, 1)
For x > 1, f(x) = 4x, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (1, ∞)
So now, as f(x) is continuous in x ∈ (-∞, 0) U (0, 1) U (1, ∞)= R – {0, 1}
Let’s check the continuity at x = 0,
Left limit = 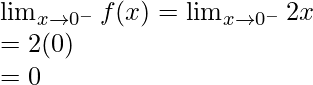
Right limit = 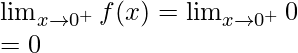
Function value at x = 0, f(0) = 0
As, ![]()
Hence, the function is continuous at x = 0.
Now, let’s check the continuity at x = 1,
Left limit = 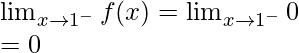
Right limit = 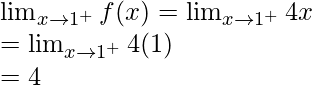
Function value at x = 1, f(1) = 0
As, ![]()
Hence, the function is discontinuous at x = 1.
Therefore, the function is continuous for only R – {1}
问题16。 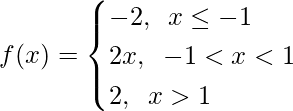
解决方案:
Here, as it is given that
For x ≤ -1, f(x) = -2, which is a constant
As constant are continuous, hence f(x) is continuous x ∈ (-∞, -1)
Now, For -1 ≤ x ≤ 1, f(x) = 2x, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (-1, 1)
For x > 1, f(x) = 2, which is a constant
As constant are continuous, hence f(x) is continuous x ∈ (1, ∞)
So now, as f(x) is continuous in x ∈ (-∞, -1) U (-1, 1) U (1, ∞)= R – {-1, 1}
Let’s check the continuity at x = -1,
Left limit = 
Right limit = 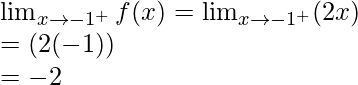
Function value at x = -1, f(-1) = -2
As, ![]()
Hence, the function is continuous at x = -1.
Now, let’s check the continuity at x = 1,
Left limit = 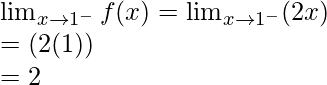
Right limit = 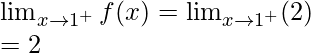
Function value at x = 1, f(1) = 2(1) = 2
As, ![]()
Hence, the function is continuous at x = 1.
Therefore, the function is continuous for any real number.
问题17:找到a和b之间的关系,以便函数f定义为
在x = 3时是连续的。
解决方案:
As, it is given that the function is continuous at x = 3.
It should satisfy the following at x = 3:
![]()
Continuity at x = 3,
Left limit = ![]()
= (a(3) + 1)
= 3a + 1
Right limit = ![]()
= (b(3) + 3)
= 3b + 3
Function value at x = 3, f(3) = a(3) + 1 = 3a + 1
So equating both the limits, we get
3a + 1 = 3b + 3
3(a – b) = 2
a – b = 2/3