第12类RD Sharma解决方案-第13章，作为费率测量工具的衍生工具–练习13.2 |套装1

问题1.方格纸的侧面以每分钟4厘米的速度增加。侧面长8厘米时，面积以什么速率增加?

解决方案：

Let the side of the square sheet be denoted by ‘a’, then area (A) of the sheet will be a² cm².

It is given that side is increasing at the rate of 4cm/min, i.e.,$\frac{\mathrm{d}a }{\mathrm{d} t}$= 4cm/min

Since, A = a²

^⇒$\frac{\mathrm{d}A }{\mathrm{d} t}$= 2a$\frac{\mathrm{d}a }{\mathrm{d} t}$

⇒$\frac{\mathrm{d}A }{\mathrm{d} t}$= 2 x 8 x 4 [ Since, a=8 and$\frac{\mathrm{d}a }{\mathrm{d} t}$= 4cm/min]

⇒$\frac{\mathrm{d}A }{\mathrm{d} t}$= 64 cm²/min

问题2.可变立方体的边缘以每秒3厘米的速度增加。边缘长10厘米时，立方体的体积增加多快?

解决方案：

Let the edge of the cube be denoted by symbol ‘a’ and volume of the cube be denoted by ‘V’.

Now, as given the edge of variable cube is increasing, i.e.,$\frac{\mathrm{d}a }{\mathrm{d} t}$= 3 cm/sec

Since, V = a³

⇒$\frac{\mathrm{d}V }{\mathrm{d} t}$= 3a²$\frac{\mathrm{d}a }{\mathrm{d} t}$

⇒$\frac{\mathrm{d}V }{\mathrm{d} t}$= 3 x 10 x 10 x 3 [Since, a=10 and$\frac{\mathrm{d}a }{\mathrm{d} t}$= 3 cm/sec]

⇒$\frac{\mathrm{d}V }{\mathrm{d} t}$= 900 cm³/sec

问题3.正方形的边以0.2厘米/秒的速度增加。求出正方形周长的增加率。

解决方案：

Let the side of the square be denoted by a cm and its perimeter (P) = 4a cm

As given, the side is increasing, i.e.,$\frac{\mathrm{d}a }{\mathrm{d} t}$= 0.2 cm/sec

Now since, P = 4a

⇒$\frac{\mathrm{d}P }{\mathrm{d} t}$= 4$\frac{\mathrm{d}a }{\mathrm{d} t}$

⇒$\frac{\mathrm{d}P }{\mathrm{d} t}$= 4 x 0.2

⇒$\frac{\mathrm{d}P }{\mathrm{d} t}$= 0. 8 cm/sec

问题4.圆的半径以0.7厘米/秒的速度增加。圆周的增长率是多少?

解决方案：

Let the radius of the circle be denoted by ‘r’ cm and its circumference is given by C = 2*$\pi$*r

Also given, the radius is increasing i.e.,$\frac{\mathrm{d}r }{\mathrm{d} t}$= 0.7 cm/sec at any time t.

Rate of increase of its circumference =$\frac{\mathrm{d}C }{\mathrm{d} t}$

⇒$\frac{\mathrm{d}C }{\mathrm{d} t}$= 2*$\pi*\frac{\mathrm{d}r }{\mathrm{d} t}$

⇒$\frac{\mathrm{d}C }{\mathrm{d} t}$= 2 * 22/7 * 0.7

⇒$\frac{\mathrm{d}C }{\mathrm{d} t}$= 4.4 cm/sec

问题5.球形soap的半径以0.2厘米/秒的速度增加。当半径为7 cm时，求出其表面积的增加率。

解决方案：

Let the radius of the spherical soap be denoted by ‘r’ and its surface area (S) = 4$\pi$r²

Also, given the radius is increasing i.e.,$\frac{\mathrm{d}r }{\mathrm{d} t}$= 0.2 cm/sec

Therefore, the increase of surface area at any time t is given by$\frac{\mathrm{d}S}{\mathrm{d} t}$

⇒$\frac{\mathrm{d}S }{\mathrm{d} t}$= 4*$\pi$*2r*$\frac{\mathrm{d}r }{\mathrm{d} t}$

⇒$\frac{\mathrm{d}S }{\mathrm{d} t}$= 8 * 22/7 * 7 * 0.2

⇒$\frac{\mathrm{d}S }{\mathrm{d} t}$= 35.2 cm²/sec

问题6.始终保持球形的气球通过每秒泵入900立方厘米的气体进行充气。求出半径为15 cm时气球半径增加的速率。

解决方案：

Let the radius of the spherical balloon be denoted by ‘r’ and volume being inflated at \frac{\mathrm{d} V}{\mathrm{d} t} = 900 cm³/sec

Since, V =$\frac{4}{3} \times \pi\times r^3$

⇒$\frac{\mathrm{d}V }{\mathrm{d} t}$=$\frac{4}{3} \times \pi\times 3r^2 \times \frac{\mathrm{d} r}{\mathrm{d} t}$

⇒$\frac{\mathrm{d}V }{\mathrm{d} t}$=$4 \times \pi\times r^2 \times \frac{\mathrm{d} r}{\mathrm{d} t}$

⇒ 900 = $4 \times \pi\times (15)^2 \times \frac{\mathrm{d} r}{\mathrm{d} t}$

⇒ 900 =900$\pi\times \frac{\mathrm{d} r}{\mathrm{d} t}$

⇒$\frac{\mathrm{d} r}{\mathrm{d} t}$=$\frac{1}{\pi}$cm/sec.

问题7.气泡的半径以0.5厘米/秒的速度增加。当半径为1 cm时，气泡的体积以什么速率增加?

解决方案：

Let the radius of the bubble be denoted by ‘r’ and its volume be denoted by V where V =$\frac{4}{3} \times \pi\times r^3$

Now at any time t, radius is increasing i.e.,$\frac{\mathrm{d} r}{\mathrm{d} t}$= 0.5 cm.sec

Therefore,$\frac{\mathrm{d} V}{\mathrm{d} t}$= 4$\pi$*r²*$\frac{\mathrm{d} r}{\mathrm{d} t}$

⇒$\frac{\mathrm{d} V}{\mathrm{d} t}$= 4$\pi$* (1)² * 0.5

⇒$\frac{\mathrm{d} V}{\mathrm{d} t}$= 2$\pi$cm³/sec

问题8. 2米高的人以6公里高的灯柱以5公里/小时的均匀速度行走。求出阴影长度增加的速率。

解决方案：

Let MN denote the vertical lamp post of height 6 meter and at any instant t, a man XY of height 2 meter be standing in front of the lamp post at a distance ‘m’ and let ‘n’ be length of his shadow. It can be seen in a figure as:

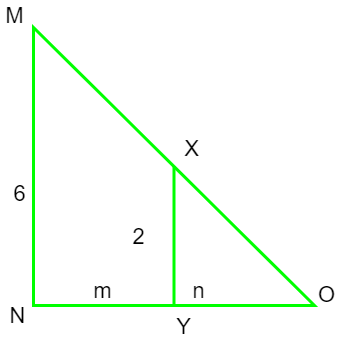
We can notice$\triangle MNO \sim \triangle XYO$

⇒$\frac{MN}{XY}$=$\frac{NO}{YO}$

⇒$\frac{6}{2}$=$\frac{m+n}{n}$

⇒ 3n = m + n

⇒ m = 2n

⇒$\frac{\mathrm{d} m}{\mathrm{d} t}$= 2$\frac{\mathrm{d} n}{\mathrm{d} t}$

⇒$\frac{\mathrm{d} n}{\mathrm{d} t}$=$\frac{5}{2}$km/hr

问题9.将一块石头掉进一个安静的湖中，海浪以4厘米/秒的速度绕圈运动。在圆波半径为10 cm的瞬间，封闭区域的增长速度有多快?

解决方案：

Let the radius of circular wave be denoted by ‘r’ and at any instant t, its radius increasing at$\frac{\mathrm{d} r}{\mathrm{d} t}$= 4 cm/sec

Now, area of circular wave (A) =$\pi$r²

⇒$\frac{\mathrm{d} A}{\mathrm{d} t}$= 2$\pi r\frac{\mathrm{d} r}{\mathrm{d} t}$

⇒$\frac{\mathrm{d} A}{\mathrm{d} t}$= 2*$\pi$*10* 4

⇒$\frac{\mathrm{d} A}{\mathrm{d} t}$= 80$\pi$cm²/sec

问题10.一个身高160厘米的人以1.1 m / sec的速度离开位于6 m高的杆顶的光源。当他离杆子1 m时，阴影的长度增加多快?

解决方案：

Let the vertical pole of light be denoted by MN and the man be denoted by XY, then his position with respect to lamp can be drawn as shown in figure:

We can notice,$\triangle MNO \sim \triangle XYO$

⇒$\frac{MN}{XY}$=$\frac{NY}{YO}$

⇒$\frac{6}{1.6}$=$\frac{x+y}{y}$

⇒$\frac{60}{16}$=$\frac{x}{y}$+ 1

⇒$\frac{x}{y}$=$\frac{60-16}{16}$

⇒$\frac{x}{y}$=$\frac{44}{16}$

⇒ y =$\frac{16}{44}x$

⇒$\frac{\mathrm{d} y}{\mathrm{d} t}$=$\frac{16}{44}(\frac{\mathrm{d} x}{\mathrm{d} t})$

⇒$\frac{\mathrm{d} y}{\mathrm{d} t}$=$\frac{16}{44}$* 1.1

⇒$\frac{\mathrm{d} y}{\mathrm{d} t}$= 0.4 m/sec

问题11：一个身高180厘米的人以2 m / sec的速度行走。远离距离地面9 m的光源。距光源3 m处的阴影长度增加多快?

解决方案：

Let MN denote the vertical lamp post of height 6 meter and at any instant t, a man XY of height 2 meter be standing in front of the lamp post at a distance ‘m’ and let ‘n’ be length of his shadow. It can be seen in a figure as:

We can notice

$\triangle MNO$∼ $\triangle XYO$

⇒$\frac{MN}{XY}$=$\frac{NO}{YO}$

⇒$\frac{9}{1.8}$= $\frac{m+n}{n}$

⇒ m = 4n

⇒$\frac{\mathrm{d} m}{\mathrm{d} t}$= 4$\frac{\mathrm{d} n}{\mathrm{d} t}$

⇒$\frac{\mathrm{d} n}{\mathrm{d} t}$=$\frac{1}{4}$x 2 [Since,$\frac{\mathrm{d} m}{\mathrm{d} t}$= 2]

⇒$\frac{\mathrm{d} n}{\mathrm{d} t}$= 0.5 m/sec

问题12。一个13 m长的梯子靠在墙上。梯子的脚以1.5 m / sec的速度沿地面拉离墙壁。当梯子的脚距墙壁12 m时，梯子与地面之间的角度θ变化多快。

解决方案：

Let the height of the wall that is leaning against a wall be denoted by y meters and the distance of the foot of ladder from base of the wall be x meters.

we can derive tan θ = y/x ⇒ y = xtan θ

Also, using Pythagoras theorem, x2 + y2 = (13)2

⇒ x² + (xtan θ )² = 169

⇒ x² (1+tan² θ ) = 169

⇒ sec² θ = 169/x²

⇒ 2 sec θ . tan θ sec θ$\frac{\mathrm{d} \theta}{\mathrm{d} t}$= 169.$(\frac{-2}{x^3}) \frac{\mathrm{d} x}{\mathrm{d} t}$

⇒$\frac{\mathrm{d} \theta}{\mathrm{d} t}$=$\frac{-338\times1.5}{12^3. 2 sec^2\theta \tan\theta}$………………(1)

Using Pythagoras Theorem, when x=12, then y=5

Therefore, sec θ = 13/12 and tan θ = 12/5

Then, equation 1 can be written as

⇒$\frac{\mathrm{d} \theta}{\mathrm{d} t}$=$\frac{-338\times 1.5}{12^3 \times 2\times (\frac{13}{12})^2\times \frac{5}{12}}$

⇒$\frac{\mathrm{d} \theta}{\mathrm{d} t}$= -0.3 rad/sec

问题13：粒子沿着曲线y = x ² + 2x移动。曲线的哪些点的x和y坐标以相同的速率变化?

解决方案：

We are given y = x² + 2x

⇒$\frac{\mathrm{d} y}{\mathrm{d} t}$= 2x$\frac{\mathrm{d} x}{\mathrm{d} t}$+ 2$\frac{\mathrm{d} x}{\mathrm{d} t}$

⇒ $\frac{\mathrm{d} y}{\mathrm{d} t}$= (2x+2)$\frac{\mathrm{d} x}{\mathrm{d} t}$

⇒ 2x + 2 = 1 [Since,$\frac{\mathrm{d} y}{\mathrm{d} t}$=$\frac{\mathrm{d} x}{\mathrm{d} t}$]

⇒ x = -1/2

Putting the value of x in our original equation, we get y= -3/4

Hence, the coordinates of the point are$\left ( \frac{-1}{2},\frac{-3}{4} \right )$

问题14.如果y = 7x – x ³并且x以每秒4个单位的速率增加，那么当x = 2时曲线的斜率变化有多快?

解决方案：

We are given y = 7x – x³

⇒$\frac{\mathrm{d} y}{\mathrm{d} x}$= 7 – 3x²

Let the slope of the curve be denoted by m, then

⇒ m = 7 – 3x²

⇒$\frac{\mathrm{d} m}{\mathrm{d} t}$= -6x$\frac{\mathrm{d} x}{\mathrm{d} t}$

⇒$\frac{\mathrm{d} m}{\mathrm{d} t}$= -6 x 4 x 2

⇒$\frac{\mathrm{d} m}{\mathrm{d} t}$= -48

Therefore, the slope of the curve is decreasing at the rate of 48 units/sec.

问题15.粒子沿着曲线y = x3移动。在曲线上找到y坐标变化比x坐标快三倍的点。

解决方案：

We are given y = x³

⇒$\frac{\mathrm{d} y}{\mathrm{d} t}$= 3x²$\frac{\mathrm{d} x}{\mathrm{d} t}$

Also, the point on y-coordinate changes 3 times more rapidly than x-coordinate, therefore

$\frac{\mathrm{d} y}{\mathrm{d} t}$= 3$\frac{\mathrm{d} x}{\mathrm{d} t}$

⇒ 3$\frac{\mathrm{d} x}{\mathrm{d} t}$= 3x²$\frac{\mathrm{d} x}{\mathrm{d} t}$

⇒ x² = 1

⇒ x = ±1

Substituting the value of x in y = x³, we get y = ±1

So, the points are (1,1) and (-1,-1).

问题16(i)找到一个角度θ，其增加速度是其余弦的两倍?

(ii)找出一个角度θ，其两倍的增加速率是其余弦的减小速率的两倍?

解决方案：

(i) Let x = cos∅

Differentiating both sides with respect to t, we get

$\frac{\mathrm{d} x}{\mathrm{d} t}$= -sin∅$\frac{\mathrm{d} \varnothing }{\mathrm{d} t}$

According to the condition given in question:

$\frac{\mathrm{d} \varnothing }{\mathrm{d} t}$= 2$\frac{\mathrm{d} x}{\mathrm{d} t}$

⇒$\frac{\mathrm{d} x }{\mathrm{d} t}$= -sin∅$(2\frac{\mathrm{d} x }{\mathrm{d} t})$

⇒ sin∅ = -1/2

⇒ ∅ = π + π/6 = 7π/6

(ii) Let x = cos∅

Differentiating both sides with respect to t, we get

$\frac{\mathrm{d} x}{\mathrm{d} t}$= -sin∅$\frac{\mathrm{d} \varnothing }{\mathrm{d} t}$

According to the condition given in question:

$\frac{\mathrm{d} \varnothing }{\mathrm{d} t}$= -2$\frac{\mathrm{d} x}{\mathrm{d} t}$

⇒$\frac{\mathrm{d} x }{\mathrm{d} t}$= -sin∅$(-2\frac{\mathrm{d} x }{\mathrm{d} t})$

⇒ sin∅ = 1/2