问题33.区分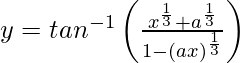 关于x。
关于x。
解决方案:
We have,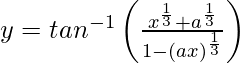
=![]()
Differentiating with respect to x, we get,
![]()
=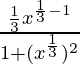
=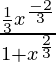
=![]()
问题34.区分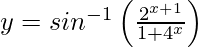 关于x。
关于x。
解决方案:
We have,![]()
On putting 2x = tan θ, we get,
![]()
=![]()
=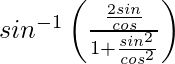
=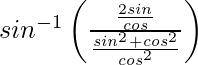
=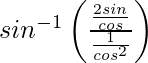
=![]()
=![]()
=![]()
= 2θ
= 2 tan−1 (2x)
Differentiating with respect to x, we get,
![]()
=![]()
=![]()
问题35.如果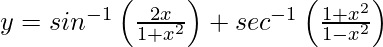 ,0
,0 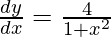 。
。
解决方案:
We have,![]()
=![]()
On putting x = tan θ, we get,
y =![]()
=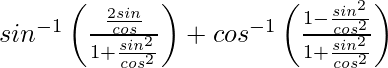
=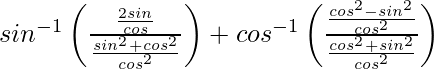
=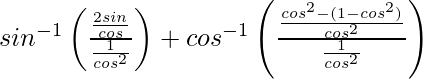
=![]()
=![]()
Now, 0 < x < 1
=> 0 < tan θ < 1
=> 0 < θ < π/4
=> 0 < 2θ < π/2
So, y = 2θ + 2θ
= 4θ
= 4 tan−1 x
Now, L.H.S. =![]()
=![]()
= R.H.S.
Hence proved.
问题36.如果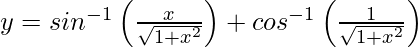 ,0
,0 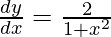 。
。
解决方案:
We have,![]()
On putting x = tan θ, we get,
![]()
=![]()
=![]()
=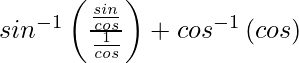
=![]()
Now, 0 < x < ∞
=> 0 < tan θ < ∞
=> 0 < θ < π/2
So, y = θ + θ
= 2θ
= 2 tan−1 x
Now, L.H.S. =![]()
=![]()
= R.H.S.
Hence proved.
问题37关于x区分以下几点:
(i)cos -1 (sin x)
解决方案:
We have, y = cos−1 (sin x)
=![]()
=![]()
Differentiating with respect to x, we get,
![]()
= 0 − 1
= −1
(ii) 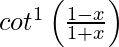
解决方案:
We have, y =![]()
On putting x = tan θ, we get,
![]()
=![]()
=![]()
=![]()
=![]()
=![]()
=![]()
Differentiating with respect to x, we get,
![]()
= 0 +![]()
=![]()
问题38.区分![由QuickLaTeX.com渲染 y=cot^{-1}\left[\frac{\sqrt{1+sinx}+\sqrt{1-sinx}}{\sqrt{1+sinx}-\sqrt{1-sinx}}\right]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20RD%20Sharma%20Solutions%20%E2%80%93%20Chapter%2011%20Differentiation%20%E2%80%93%20Exercise%2011.3%20%7C%20Set%203_57.jpg) ,相对于x ,0
,相对于x ,0 π/ 2。
解决方案:
We have,![]()
=![]()
=![]()
=![]()
=![]()
=![]()
=![Rendered by QuickLaTeX.com cot^{-1}\left[\frac{2cos^2\frac{x}{2}}{2sin\frac{x}{2}cos\frac{x}{2}}\right]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20RD%20Sharma%20Solutions%20%E2%80%93%20Chapter%2011%20Differentiation%20%E2%80%93%20Exercise%2011.3%20%7C%20Set%203_64.jpg)
=![]()
=![]()
Differentiating with respect to x, we get,
![]()
=![]()
问题39.如果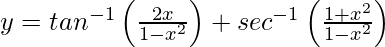 ,x> 0,证明
,x> 0,证明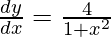 。
。
解决方案:
We have,![]()
=![]()
On putting x = tan θ, we get,
y =![]()
=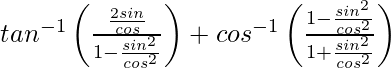
=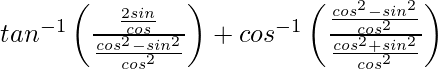
=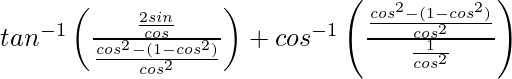
=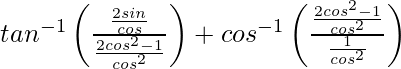
=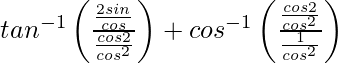
=![]()
=![]()
=![]()
Here, 0 < x < ∞
=> 0 < tan θ < ∞
=> 0 < θ < π/2
=> 0 < 2θ < π
So, y = 2θ + 2θ
= 4θ
= 4 tan−1 x
Now, L.H.S. =![]()
=![]()
= R.H.S.
Hence proved.
问题40.如果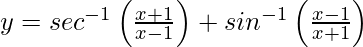 ,x> 0,找到
,x> 0,找到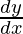 。
。
解决方案:
We have,![]()
=![]()
=![]()
Differentiating with respect to x, we get,
![]()
= 0
问题41.如果![由QuickLaTeX.com渲染 y=sin\left[2tan^{-1}\sqrt{(\frac{1-x}{1+x})}\right]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20RD%20Sharma%20Solutions%20%E2%80%93%20Chapter%2011%20Differentiation%20%E2%80%93%20Exercise%2011.3%20%7C%20Set%203_90.jpg) , 找
, 找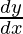 。
。
解决方案:
We have,![]()
On putting x = cos 2θ, we get,
![]()
=![Rendered by QuickLaTeX.com sin\left[2tan^{-1}\sqrt{(\frac{2sin^2θ}{2cos^2θ})}\right]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20RD%20Sharma%20Solutions%20%E2%80%93%20Chapter%2011%20Differentiation%20%E2%80%93%20Exercise%2011.3%20%7C%20Set%203_94.jpg)
=![]()
=![]()
=![]()
=![]()
=![]()
=![]()
=![]()
Differentiating with respect to x, we get,
![]()
=![]()
=![]()
问题42.如果 ,0
,0 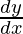 。
。
解决方案:
We have,![]()
On putting 2x = cos θ, we get,
![]()
=![]()
=![]()
Now, 0 < x < 1/2
=> 0 < 2x < 1
=> 0 < cos θ < 1
=> 0 < θ < π/2
and 0 > −θ > −π/2
=> π/2 > (π/2 −θ) > 0
So, y =![]()
= π − θ
= π − cos−1 (2x)
Differentiating with respect to x, we get,
![]()
=
=![]()
问题43.如果tan -1 (a + bx)的导数在x = 0时取值为1,则证明1 + a 2 = b。
解决方案:
We have, y = tan−1 (a + bx)
Differentiating with respect to x, we get,
![]()
=![]()
At x = 0, we have,
=>![]() = 1
= 1
=>![]() = 1
= 1
=> 1 + a2 = b
Hence proved.
问题44.如果 ,−1/2
,−1/2 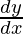 。
。
解决方案:
We have,![]()
On putting 2x = cos θ, we get,
![]()
=![]()
=![]()
Now, −1/2 < x < 0
=> −1 < 2x < 0
=> −1 < cos θ < 0
=> π/2 < θ < π
and −π/2 > −θ > −π
=> 0 > (π/2 −θ) > −π/2
So, y =![]()
= −π + 3θ
= −π + 3 cos−1 (2x)
Differentiating with respect to x, we get,
![]()
= 0 +![]()
=![]()
问题45.如果 , 找
, 找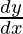 。
。
解决方案:
We have,![]()
On putting x = cos 2θ, we get,
![]()
=![]()
=![]()
=
=![]()
=![]()
=![]()
=![]()
=![]()
Differentiating with respect to x, we get,
![]()
= 0 −![]()
=![]()
问题46.如果 , 找
, 找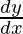 。
。
解决方案:
We have,![]()
On putting x = cos θ, we get,
![]()
=![]()
=![]()
Let![]()
=> sin Ø =![]()
=> sin Ø =
=> sin Ø =![]()
=> sin Ø =![]()
=> sin Ø =![]()
So, y =![]()
=![]()
= Ø + θ
=![]()
Differentiating with respect to x, we get,
![]()
= 0 +![]()
=![]()
问题47.区分![由QuickLaTeX.com渲染 y=sin^{-1}\left[\frac{2^{x+1}×3^x}{1+(36)^x}\right]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20RD%20Sharma%20Solutions%20%E2%80%93%20Chapter%2011%20Differentiation%20%E2%80%93%20Exercise%2011.3%20%7C%20Set%203_162.jpg) 关于x。
关于x。
解决方案:
We have,![]()
=![]()
=![]()
On putting 6x = tan θ, we get,
=![]()
=![Rendered by QuickLaTeX.com sin^{-1}\left[\frac{\frac{2sinθ}{cosθ}}{1+\frac{sin^2θ}{cos^2θ}}\right]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20RD%20Sharma%20Solutions%20%E2%80%93%20Chapter%2011%20Differentiation%20%E2%80%93%20Exercise%2011.3%20%7C%20Set%203_167.jpg)
=![Rendered by QuickLaTeX.com sin^{-1}\left[\frac{\frac{2sinθ}{cosθ}}{\frac{cos^2θ+sin^2θ}{cos^2θ}}\right]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20RD%20Sharma%20Solutions%20%E2%80%93%20Chapter%2011%20Differentiation%20%E2%80%93%20Exercise%2011.3%20%7C%20Set%203_168.jpg)
=![Rendered by QuickLaTeX.com sin^{-1}\left[\frac{\frac{2sinθ}{cosθ}}{\frac{1}{cos^2θ}}\right]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20RD%20Sharma%20Solutions%20%E2%80%93%20Chapter%2011%20Differentiation%20%E2%80%93%20Exercise%2011.3%20%7C%20Set%203_169.jpg)
=![]()
=![]()
=![]()
= 2θ
= 2 tan−1 (6x)
Differentiating with respect to x, we get,
![]()
=![]()
=![]()