第12类RD Sharma解决方案–第24章标量或点积–练习24.2

问题1.在三角形OAB中，如果P，Q是AB的三等分点，则证明OP ² + OQ ² = 5/9 AB ² 。

解决方案：

Given that in triangle OAB, 

∠AOB = 90°, and P, Q are points of trisection of AB.

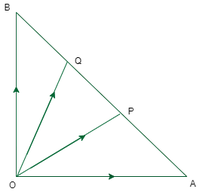
Consider ‘O’ as origin, the position vectors of A and B are $\vec{a}$ and $\vec{b}$ respectively.

Since P and Q are points of trisection of AB, AP:PB = 1:2 and AQ:QB = 2:1.

From section formula position vector of P is $\vec{OP}=\frac{2\vec{a}+\vec{b}}{3}$

Position vector of Q is $\vec{OQ}=\frac{\vec{a}+2\vec{b}}{3}$

Now, OP² + OQ² = $|\overrightarrow{OP}|^2+|\overrightarrow{OQ}|^2$

⇒ $(\frac{2\vec{a}+\vec{b}}{3}).(\frac{2\vec{a}+\vec{b}}{3})+(\frac{\vec{a}+2\vec{b}}{3}).(\frac{\vec{a}+2\vec{b}}{3})$

⇒ $\frac{4|\vec{a}|^2+4\vec{a}.\vec{b}+|\vec{b}|^2+|\vec{a}|^2+4\vec{a}.\vec{b}+4|\vec{b}|^2}{9}$

We know that $\vec{a}.\vec{b}=0$, since $\vec{a}$ and $\vec{b}$ are perpendicular.

⇒ $\frac{5}{9}[|\vec{a}|^2+|\vec{b}|^2]$

By using Pythagoras theorem, we get

$\frac{5}{9}|\overrightarrow{AB}|^2$

Hence proved.

问题2.证明如果四边形的对角线彼此成直角一分为二，那么它就是菱形。

解决方案：

Let us considered OABC be quadrilateral and the diagonals AB and OC bisect each other at 90°.

Consider ‘0’ as origin and the position vectors of A and B are given by $\vec{a}$ and $\vec{b}$ respectively.

Now, Position vector of E is $\overrightarrow{OE}=\frac{\vec{a}+\vec{b}}{2}$

Using triangle law of vector addition, $\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}$

⇒ $\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$ 

⇒ $\overrightarrow{AB}=\vec{b}-\vec{a}$

Since the diagonal bisect each other at 90°, $\vec{AB}.\vec{OC}=0$

⇒ $(\vec{b}-\vec{a}).(\vec{b}-\vec{a})=0$

⇒ $|\vec{b}|^2-|\vec{a}|^2=0$ 

⇒ |a| = |b|

⇒ OA = OB

Therefore, we proved that adjacent sides of quadrilateral are equal, if its diagonals bisect each other at 90°. 

问题3.通过矢量方法证明，在直角三角形中，斜边的平方等于其他两侧的平方和(毕达哥拉斯定理)。

解决方案：

Let us considered ABC be the right angled triangle with ∠BAC = 90°.

Consider ‘A’ as origin and the position vectors $AB=\vec{b},AC=\vec{c}$

Since AB and AC are perpendicular to each other, $\vec{a}.\vec{b}=0$

Now, AB² + AC² = $|\vec{b}|^2+|\vec{c}|^2$ …(1)

From triangle law of vector addition, $\overrightarrow{AC}^2=\overrightarrow{AB}^2+\overrightarrow{BC}^2$

⇒ $\overrightarrow{BC}^2=\overrightarrow{AC}^2-\overrightarrow{AB}^2$

⇒ $\overrightarrow{BC}^2=\vec{c}^2-\vec{b}^2$

Now, BC² = $|\overrightarrow{BC}|^2=|\vec{c}-\vec{b}|^2$

⇒ $(\vec{c}-\vec{b}).(\vec{c}-\vec{b})$

⇒ $|\vec{c}|^2+|\vec{b}|^2-2\vec{c}.\vec{b}$ 

⇒ $|\vec{c}|^2+|\vec{b}|^2$  …(2)

Therefore, from eq(1) and eq(2) we get,

⇒ AB² + AC² = BC² 

Hence proved.

问题4：通过矢量方法证明平行四边形的对角线平方和等于其边的平方和。

解决方案：

Let us considered ABCD be a parallelogram and AC, BD are its diagonals.

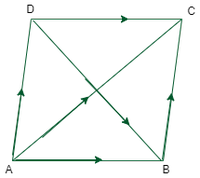
Consider A as origin, Let the position vectors of AB, AD are $\vec{b},\vec{d}$ respectively.

Using triangle law of vector addition, we have $\overrightarrow{AD}+\overrightarrow{DB}=\overrightarrow{AB}$

⇒ $\overrightarrow{DB}=\overrightarrow{AB}-\overrightarrow{AD}$

⇒ $\overrightarrow{DB}=\vec{b}-\vec{d}$

In triangle ABC, 

$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}=\vec{b}+\vec{d}$

Now, Squares of sides of parallelogram = AB² + BC² + CD² + DA²

⇒ $|\overrightarrow{AD}|^2+|\overrightarrow{AB}|^2+|\overrightarrow{-AB}|^2+|-\overrightarrow{AD}|^2$

⇒ $2|\overrightarrow{AB}|^2+2|\overrightarrow{AD}|^2$

⇒ $2|\vec{b}|^2+2|\vec{d}|^2$   …(1)

Also, Squares of diagonals = DB² + AC²

⇒ $|\overrightarrow{DB}|^2+|\overrightarrow{AC}|^2$

⇒ $|\vec{b}|^2-2\vec{b}.\vec{d}+|\vec{d}|^2+|\vec{b}|^2+2\vec{b}.\vec{d}+|\vec{d}|^2$

⇒ $2|\vec{b}|^2+2|\vec{d}|^2$   …(2)

By, observing eq(1) and eq(2), 

We proved that sum of squares of sides of a parallelogram is equal to sum of squares of its diagonals.

问题5.使用矢量方法证明通过将矩形相邻边的中点连接在一起而得到的四边形是菱形。

解决方案：

Let us considered ABCD is a rectangle and P, Q, R, S are midpoints of AB, BC, CD, DA respectively.

Consider A as origin, the position vectors of AB, AD are $\vec{b},\vec{d}$respectively.

Now, Using triangle law of vector addition, $\overrightarrow{PQ}=\overrightarrow{PB}+\overrightarrow{BQ}$

⇒ $\frac{\overrightarrow{AB}}{2}+\frac{\overrightarrow{BC}}{2}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{BC})$

⇒ $\overrightarrow{PQ}=\frac{1}{2}(\overrightarrow{AC})$

Similarly, 

$\overrightarrow{SR}=\overrightarrow{SD}+\overrightarrow{DR}$

⇒ $\frac{\overrightarrow{AD}}{2}+\frac{\overrightarrow{DC}}{2}=\frac{1}{2}(\overrightarrow{AD}+\overrightarrow{DC})$

⇒$\overrightarrow{SR}=\frac{1}{2}(\overrightarrow{AC})$

By observing, we find that PQ || SR, so we can say it is a parallelogram

Let us find if it forms a rhombus by calculating length of adjacent sides,

⇒ $|\overrightarrow{PQ}|^2=\frac{1}{4}|\overrightarrow{AC}|^2$  …(1)

Also, from figure, $\overrightarrow{PS}=\overrightarrow{AS}-\overrightarrow{PA}$

⇒ $\frac{\overrightarrow{AD}}{2}-\frac{-\overrightarrow{AB}}{2}=\frac{1}{2}(\overrightarrow{AD}+\overrightarrow{AB})$

⇒ $\overrightarrow{PS}=\frac{1}{2}(\overrightarrow{AC})$

⇒ $|\overrightarrow{PS}|^2=\frac{1}{4}(|\overrightarrow{AC}|^2)$  …(2)

From eq(1) and eq(2) PQ and PS are adjacent sides and |PQ|=|PS|, 

so PQRS is a Rhombus.

Therefore, Hence proved

问题6：证明菱形的对角线是彼此垂直的等分线。

解决方案：

Let us considered OABC be a Rhombus, OB and AC are diagonals of Rhombus.

Consider O as origin, position vectors of OA and OC are $\vec{a},\vec{c}$respectively.

From figure, $\overrightarrow{OB} = \overrightarrow{OA}+\overrightarrow{AB}$

⇒ $\overrightarrow{OB} = \vec{a}+\vec{c}$

From figure, $\overrightarrow{OC} = \overrightarrow{OA}+\overrightarrow{AC}$

⇒ $\overrightarrow{AC} = \vec{c}-\vec{a}$

Now, $\overrightarrow{OB}.\overrightarrow{AC}=(\vec{c}+\vec{a}).(\vec{c}-\vec{a})$

⇒ $|\vec{c}|^2-|\vec{a}|^2$

We know, that adjacent sides are equal in a Rhombus, 

⇒ $\overrightarrow{OB}.\overrightarrow{AC}=|\vec{c}|^2-|\vec{a}|^2=0$

Therefore, diagonals of rhombus are perpendicular bisectors of each other.

问题7：证明且仅当矩形是正方形时，矩形的对角线才是垂直的。

解决方案：

Let us considered ABCD is a rectangle, AC, BD are diagonals of rectangle.

Consider A as origin, Position vectors of AB, AD are $\vec{b},\vec{d}$respectively.

From figure, $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}$

⇒ $\overrightarrow{AC}=\vec{b}+\vec{d}$

Similarly, $\vec{AD}=\vec{AB}+\vec{BD}$

⇒ $\overrightarrow{BD}=\vec{d}-\vec{b}$

If the diagonals are perpendicular, then $\overrightarrow{AC}.\overrightarrow{BD}=0$

⇒ $(\vec{b}+\vec{d}).(\vec{b}-\vec{d})=0$

⇒ $|\vec{b}|^2-|\vec{d}|^2=0$

⇒ $|\vec{b}|=|\vec{d}|$

Therefore, If the diagonals of rectangle are perpendicular, Then it is a square.

问题8.如果AD是三角形ABC的中位数，则使用矢量证明AB ² + AC ² = 2(AD ² + CD ² )。

解决方案：

Let us considered ABC is a triangle and AD is median.

Consider A is a origin, position vectors of AB and AC are $\vec{b},\vec{c}$respectively.

Position vector of AD is $\overrightarrow{AD}=\frac{\vec{b}+\vec{c}}{2}$

Position vector of CD is $\overrightarrow{CD}=\overrightarrow{AD}-\overrightarrow{AC}$

⇒ $\overrightarrow{CD}=\frac{\vec{b}+\vec{c}}{2}-\vec{c}=\frac{\vec{b}-\vec{c}}{2}$

Now, AB² + AC² = $|\overrightarrow{AB}|^2+|\overrightarrow{AC}|^2=|\vec{b}|^2+|\vec{c}|^2$ …(1)

Also, 2(AD² + CD²) = $2(|\vec{AD}|^2+|\vec{CD}|^2)$

⇒ $2(\frac{|\vec{b}|^2+|\vec{c}|^2+2\vec{b}.\vec{c}}{2}+\frac{|\vec{b}|^2+|\vec{c}|^2-2\vec{b}.\vec{c}}{2})$

⇒ $|\vec{b}|^2+|\vec{c}|^2$ …(2)

From eq(1) and eq(2), we get

AB² + AC² = 2(AD² + CD²)

Therefore, Hence proved.

问题9.如果三角形底边的中值垂直于底边，则三角形为等腰。

解决方案：

Let us considered ABC be a triangle and AD is median.

Consider A as origin, position vector of AB, AC are $\vec{b},\vec{c}$respectively.

Now, position vector of AD is $\overrightarrow{AD}=\frac{\vec{b}+\vec{c}}{2}$

Using triangle law of vector addition, $\overrightarrow{AC}=\overrightarrow{BC}+\overrightarrow{AB}$

⇒ $\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}=\vec{c}-\vec{b}$

Since, AD and BC are perpendicular, $\overrightarrow{BC}.\overrightarrow{AD}=0$

⇒ $(\vec{c}-\vec{b}).\frac{\vec{b}+\vec{c}}{2}=0$

⇒ $(\vec{c}-\vec{b}).(\vec{c}+\vec{b})=0$

⇒ $|\vec{c}|^2-|\vec{b}|^2=0$

⇒ $|\vec{c}|=|\vec{b}|$ 

⇒ AC = AB

Therefore, Triangle ABC is an Isosceles triangle.

问题10.在四边形ABCD中，证明AB ² + BC ² + CD ² + DA ² = AC ² + BD ² + 4PQ ² ，其中P，Q是对角线AC和BD的中点。

解决方案：

Let us considered ABCD be a quadrilateral, AC, BD are diagonals.

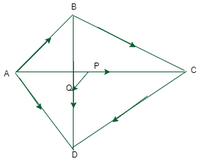
Consider A as origin, the position vectors of AB, AC, AD are $\vec{b},\vec{c},\vec{d}$respectively.

Let P and Q are midpoints of AC, BD.

Position vector of P is $\frac{\overrightarrow{AC}}{2}=\frac{\vec{c}}{2}$

Position vector of Q is $\frac{\vec{b}+\vec{d}}{2}$

Now, AB² + BC² + CD² + DA² = $|\overrightarrow{AB}|^2+|\overrightarrow{BC}|^2+|\overrightarrow{CD}|^2+|\overrightarrow{DA}|^2$

⇒ $|\vec{b}|^2+|\vec{c}-\vec{b}|^2+|\vec{d}-\vec{c}|^2+|\vec{d}|^2$

⇒ $2|\vec{b}|^2+2|\vec{c}|^2+2|\vec{d}|^2-2\vec{b}.\vec{c}-2\vec{c}.\vec{d}$  …(1)

Also, AC² + BD² + 4PQ² = $|\overrightarrow{AC}|^2+|\overrightarrow{BD}|^2+4|\overrightarrow{PQ}|^2$

⇒ $|\vec{c}|^2+|\vec{d}-\vec{b}|^2+4|\frac{|\vec{b}+\vec{d}|^2}{2}-\frac{|\vec{c}|^2}{2}|^2$

⇒ $|\vec{c}|^2+|\vec{d}-\vec{b}|^2+|\vec{b}+\vec{d}|^2-2|\vec{b}+\vec{d}|.|\vec{c}|+|\vec{c}|^2$

⇒ $2|\vec{b}|^2+2|\vec{c}|^2+2|\vec{d}|^2-2\vec{b}.\vec{c}-2\vec{c}.\vec{d}$   …(2)

 From eq(1) and eq(2), we get, 

AB² + BC² + CD² + DA² = AC² + BD² + 4PQ²

Therefore, Hence proved.