8类RD Sharma解决方案-第16章理解形状的四边形–练习16.1 |套装2

第16章理解形状的四边形–练习16.1 |套装1

问题13.在图中，找到∠MPN的量度。

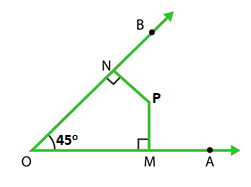
解决方案：

As we know that Sum of angles of a quadrilateral is = 360°

In the quadrilateral MPNO

∠NOP = 45°, ∠OMP = ∠PNO = 90° (Given)

Let us assume that angle ∠MPN is x°

∠NOP + ∠OMP + ∠PNO + ∠MPN = 360°

45° + 90° + 90° + x° = 360°

x° = 360° – 225°

x° = 135°

Hence, Measure of ∠MPN is 135°

问题14.四边形的边是按顺序产生的。四个外角的总和是多少?

解决方案：

As we know that, exterior angle + interior adjacent angle = 180° (Linear pair)

Applying relation for polygon having n sides

Sum of all exterior angles + Sum of all interior angles = n × 180°

Sum of all exterior angles = n × 180° – Sum of all interior angles

= n × 180° – (n -2) × 180° (Sum of interior angles is = (n – 2) x 180°)

= n × 180° – n × 180° + 2 × 180°

= 180°n – 180°n + 360° = 360°

Hence, Sum of four exterior angles is 360^o

问题15。在图中，∠A和∠B的等分线在点P处相遇。如果∠C= 100°且∠D= 50°，则求出∠APB的度量。

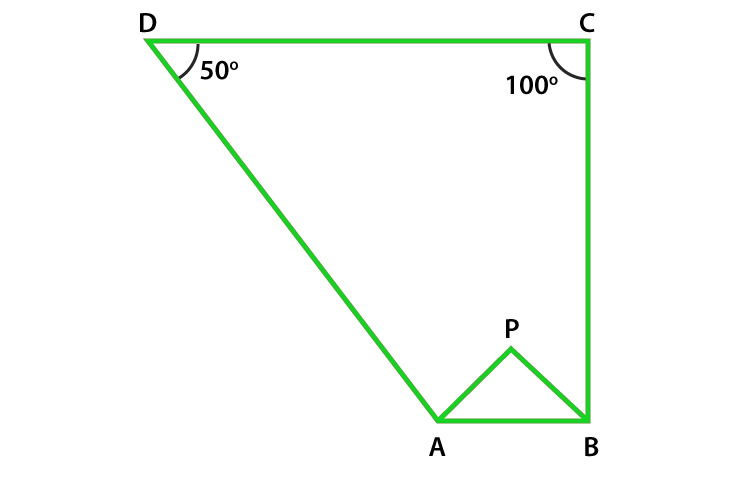
解决方案：

As we know that Sum of angles of a quadrilateral is = 360°

In the quadrilateral ABCD

Given that,

∠C =100° and ∠D = 50°

∠A + ∠B + ∠C + ∠D = 360^o

∠A + ∠B + 100^o + 50^o = 360^o

∠A + ∠B = 360^o – 150^o

∠A + ∠B = 210^o (Equation 1)

Now in Δ APB

½ ∠A + ½ ∠B + ∠APB = 180^o (sum of triangle is 180^o)

∠APB = 180^o – ½ (∠A + ∠B) (Equation 2)

On substituting value of ∠A + ∠B = 210 from equation (1) in equation (2)

∠APB = 180^o – ½ (210^o)

= 180^o – 105^o = 75^o

Hence, the measure of ∠APB is 75^o.

问题16：在四边形ABCD中，角度A，B，C和D的比例为1：2：4：5。求出四边形的每个角度的大小。

解决方案：

As we know that Sum of angles of a quadrilateral is = 360°

Let each angle be x^o

Therefore,

x^o + 2x^o + 4x^o + 5x^o = 360^o

12x^o = 360^o

x^o = 360^o/12 = 30^o

Value of angles are as x = 30^o,

2x = 2 × 30 = 60^o

4x = 4 × 30 = 120^o

5x = 5 × 30 = 150^o

Hence, Value of angles are 30^o, 60^o, 120^o, 150^o.

问题17：在四边形ABCD中，CO和DO分别是∠C和∠D的等分线。证明∠COD= 1/2(∠A+∠B)。

解决方案：

As we know that sum of angles of a quadrilateral is 360°

In the quadrilateral ABCD

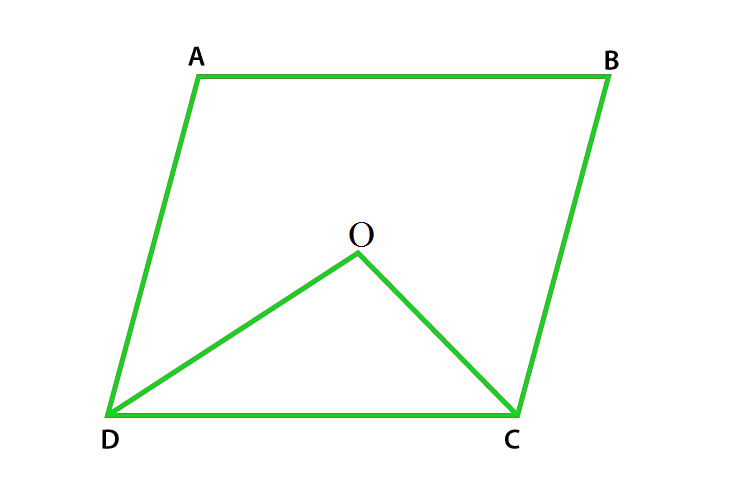
Therefore,

∠A + ∠B + ∠C + ∠D = 360^o

∠A + ∠B = 360o – (∠C + ∠D)

½ (∠A + ∠B) = ½ [360^o – (∠C + ∠D)]

= 180^o – ½ (∠C + ∠D) (Equation 1)

Now in Δ DOC

½ ∠D + ½ ∠C + ∠COD = 180^o (We know that sum of triangle = 180o)

½ (∠C + ∠D) + ∠COD = 180^o

∠COD = 180^o – ½ (∠C + ∠D) (Equation 2)

In equations (1) and (2) RHS is equal then LHS will also equal.

Hence, ∠COD = ½ (∠A + ∠B) is proved.

问题18：在规则多边形的每个角度均具有一个度量时，求出多边形的边数

(i)160°

(ii)135度

(iii)175°

(iv)162度

(v)150度

解决方案：

The sum of interior angle A of a polygon of n sides is given by A = [(n-2) ×180o] /n

(i) 160^o

Angle of quadrilateral is 160° (Given)

160^o = [(n-2) ×180^o]/n

160^on = (n-2) ×180^o

160^on = 180^on – 360^o

180^on – 160^on = 360^o

20^on = 360^o

n = 360^o/20 = 18

Hence Number of sides are 18

(ii) 135^o

Angle of quadrilateral is 135° (Given)

135^o = [(n-2) ×180^o]/n

135^on = (n-2) ×180^o

135^on = 180^on – 360^o

180^on – 135^on = 360^o

45^on = 360^o

n = 360^o / 45 = 8

Hence Number of sides are 8

(iii) 175^o

Angle of quadrilateral is 175° (Given)

175^o = [(n-2) ×180^o]/n

175^on = (n-2) ×180^o

175^on = 180^on – 360^o

180^on – 175^on = 360^o

5^on = 360^o

n = 360^o/5 = 72

Hence Number of sides are 72

(iv) 162^o

Angle of quadrilateral is 162° (Given)

162^o = [(n-2) ×180^o]/n

162^on = (n-2) ×180^o

162^on = 180^on – 360^o

180^on – 162^on = 360^o

18^on = 360^o

n = 360^o/18 = 20

Hence Number of sides are 20

(v) 150^o

Angle of quadrilateral is 160° (Given)

150^o = [(n-2) ×180^o]/n

150^on = (n-2) ×180^o

150^on = 180^on – 360^o

180^on – 150^on = 360^o

30^on = 360^o

n = 360^o/30 = 12

Hence Number of sides are 12

问题19：找出正五边形的每个外角的度数。

解决方案：

As we know that the sum of exterior angles of a polygon is 360°

Sum of each exterior angle of a polygon = 360^o/n (n is the number of sides)

As we know that number of sides in a pentagon is 5

Sum of each exterior angle of a pentagon = 360^o/5 = 72^o

Hence Measure of each exterior angle of a pentagon is 72^o

问题20.六边形的角度量度为x°，(x-5)°，(x-5)°，(2x-5)°，(2x-5)°，(2x + 20)°。求x的值。

解决方案：

As we know that the sum of interior angles of a polygon = (n – 2) × 180° (n = number of sides of polygon)

As we know that hexagon has 6 sides therefore,

The sum of interior angles of a hexagon = (6 – 2) × 180° = 4 × 180° = 720°

x°+ (x-5)°+ (x-5)°+ (2x-5)°+ (2x-5)°+ (2x+20)° = 720°

x°+ x°- 5°+ x° – 5°+ 2x° – 5°+ 2x° – 5°+ 2x° + 20° = 720°

9x° = 720°

x = 720^o/9 = 80^o

Hence Value of x is 80^o

问题21.在凸六边形中，证明所有内角的总和等于通过以相同顺序产生边而形成的外角之和的两倍。

解决方案：

As we know that the sum of interior angles of a polygon = (n – 2) × 180°

The sum of interior angles of a hexagon = (6 – 2) × 180° = 4 × 180° = 720°

Sum of exterior angle of a polygon is 360°

Hence Sum of interior angles of a hexagon = Twice the sum of interior angles.

Hence proved.

问题22：多边形的内角之和是其外角之和的三倍。确定多边形的边数。

解决方案：

As we know that the sum of interior angles of a polygon = (n – 2) × 180° (i)

The Sum of exterior angle of a polygon is 360°

therefore,

Sum of Interior Angles = 3 × sum of exterior angles

= 3 × 360° = 1080° (ii)

Now by equating (i) and (ii) we get,

(n – 2) × 180° = 1080°

n – 2 = 1080^o/180^o

n – 2 = 6

n = 6 + 2 = 8

Hence Number of sides of a polygon is 8.

问题23.确定多边形的外角和内角之比为1：5的边数。

解决方案：

As we know that the sum of interior angles of a polygon = (n – 2) × 180° (i)

The Sum of exterior angle of a polygon is 360°

As we know that Sum of exterior angles / Sum of interior angles = 1/5 (ii)

By equating (i) and (ii) we get,

360^o/(n – 2) × 180° = 1/5

(n – 2) × 180° = 360^o × 5

(n – 2) × 180° = 1800^o

(n – 2) = 1800^o/180^o

(n – 2) = 10

n = 10 + 2 = 12

Hence Numbers of sides of a polygon is 12.

问题24. PQRSTU是一个正六边形，确定每个ΔPQT的角度。

解决方案：

As we know that the sum of interior angles of a polygon = (n – 2) × 180°

The sum of interior angles of a hexagon = (6 – 2) × 180° = 4 × 180° = 720°

Sum of each angle of hexagon = 720^o/6 = 120^o

∠PUT = 120^o Proved.

In Δ PUT

∠PUT + ∠UTP + ∠TPU = 180^o (sum of triangles)

120o + 2∠UTP = 180^o (Since Δ PUT is an isosceles triangle )

2∠UTP = 180^o – 120^o

2∠UTP = 60^o

∠UTP = 60^o/2 = 30^o

∠UTP = ∠TPU = 30^o similarly ∠RTS = 30^o

therefore ∠PTR = ∠UTS – ∠UTP – ∠RTS

= 120^o – 30^o – 30^o = 60^o

∠TPQ = ∠UPQ – ∠UPT

= 120^o – 30^o = 90^o

∠TQP = 180^o – 150^o = 30^o (By using angle sum property of triangle in ΔPQT)

Hence ∠P = 90^o, ∠Q = 60^o, ∠T = 30^o