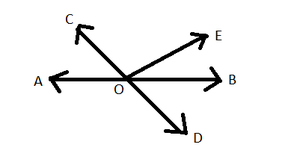
问题1.在给定图中,线AB和CD在O处相交。如果∠AOC+∠BOE= 70°,而∠BOD= 40°,找到findBOE和反射∠COE?
解决方案:
Given, AB and CD are straight lines.
∠AOC + ∠BOE = 70° —-eq(i)
∠BOD = 40° —-eq(ii)
Since, AB is a straight line, the sum of all angles made on it is 180°
=> ∠AOC + ∠COE + ∠BOE = 180° —eq(iii)
We can rearrange this equation as,
=> ∠AOC + ∠BOE + ∠COE = 180°
=> 70° + ∠COE = 180° —from eq(i)
=> ∠COE = 180° – 70° = 110°
=> ∠COE = 110° —eq(iv)
Reflex ∠COE = 360° – ∠COE = 360° – 110° = 250°
Now, it is also given that CD is also a straight line, so the sum of all angles made on it is 180°
=> ∠COE + ∠BOE + ∠BOD = 180° —eq(v)
We can rearrange this equation as,
=> ∠COE + ∠BOD + ∠BOE = 180°
=> 110° + 40° + ∠BOE = 180° —from eq(ii) and eq(iv)
=> 150° + ∠BOE = 180°
=> ∠BOE = 180° – 150° = 30°
=> ∠BOE = 30°
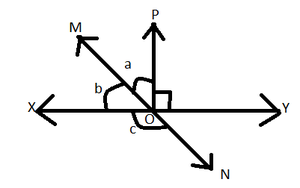
问题2。在给定图中,XY和MN线在O处相交。如果∠POY= 90°且a:b = 2:3,则找到c?
解决方案:
Given, XY and MN are straight lines.
∠POY = 90° –eq(i)
a : b = 2 : 3 –eq(ii)
∠POM = a
∠XOM = b
∠XON = c
Taking XY as a straight line, so the sum of all angles made on it is 180°
=> ∠XOM + ∠POM + ∠POY = 180° —eq(iii)
=> b + a + 90° = 180°
=> 3x + 2x + 90° = 180° from eq(i) and eq(ii)
=> 5x + 90° = 180°
=> 5x = 180° – 90° = 90°
=> 5x = 90°
=> x = 18°
a : b = 2x : 3x = 2×18 : 3×18
a = 36°
b = 54°
Taking MN as a straight line so,the sum of all the angles made on it is 180°
=> ∠XOM + ∠XON = 180°
=> 54° + ∠XON = 180° from above finding value
=> ∠XON = 126° or c = 126°
问题3。在给定的图中,QRPQR =∠PRQ,然后证明∠PQS=∠PRT?

解决方案:
Given, ∠PQR = ∠PRQ
Taking ST is a straight line, so the sum of all angles made on it is 180°
=> ∠PQS + ∠PQR = 180° —-eq(i)
also, ∠PRQ + ∠PRT = 180° —eq(ii)
By equationg both the equations because RHS of both the equation is equal So, LHS will also be equal.
=> ∠PQS + ∠PQR = ∠PRQ + ∠PRT
=> ∠PQS + ∠PQR = ∠PQR + ∠PRT –[ Given in question ∠PQR = ∠PRQ ]
=> ∠PQS = ∠PRT
问题4.在给定图中,如果x + y = w + z,则证明AOB是一条线?

解决方案:
Given, x + y = w + z –eq(i)
We know that , sum of all angles made along a point is 360°
So, Taking O as a point ∠AOC + ∠BOC + ∠BOD + ∠AOD = 360°
=> y + x + w + z = 360° from the given figure
=> (x + y) + (x + y) = 360° from eq(i)
=> 2x + 2y = 360°
=> 2(x + y) = 360°
=> x + y=180°
From this statement it is proved that AOB is a straight line because the sum of angles made on the line is 180°. So, AOB is a straight line.
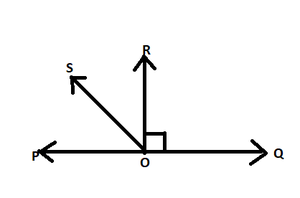
问题5.在给定图中,POQ是一条线。射线OR垂直于线PQ。 OS是位于射线OP和OR之间的另一条射线。证明∠ROS=(1/2)(∠QOS–∠POS)?
解决方案:
Given POQ is a straight line
So, the sum of all angles made on it is 180°
=> ∠POS + ∠ROS + ∠ROQ = 180°
=> ∠POS + ∠ROS + 90° = 180° [given ∠ROQ = 90°]
=> ∠POS + ∠ROS = 90°
=> ∠ROS = 90° – ∠POS –eq(i)
Now, ∠ROS + ∠ROQ = ∠QOS [from figure]
=> ∠ROS + 90° = ∠QOS
=> ∠ROS = ∠QOS – 90° –eq(ii)
Now Adding both the equations eq(i) + eq(ii)
=> ∠ROS + ∠ROS = 90° – ∠POS + ∠QOS – 90°
=> 2∠ROS =(∠QOS – ∠POS)
=> ∠ROS = (1/2) (∠QOS – ∠POS)
Hence Verified!!!
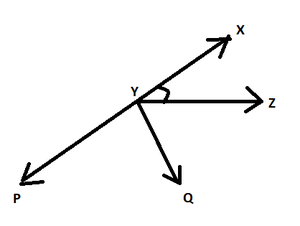
问题6.假定∠XYZ= 64°,并且XY指向P点。从给定的信息中绘制一个图形。如果射线YQ对分∠ZYP,请找到∠XYQ和反射∠QYP?
解决方案:
From the drawn figure, it is clearly shown that XYP is a straight line.
So, ∠XYZ + ∠ZYQ + ∠QYP = 180°
=> 64°+ ∠ZYQ + ∠QYP = 180° [ given ∠XYZ = 64°]
=> 64° + 2∠QYP = 180° [ YQ bisect ∠ZYP so, ∠QYP = ∠ZYQ]
=> 2∠QYP = 180° – 64° = 116°
=> ∠QYP = 58°
So, Reflex ∠QYP = 360° – 58° = 302°
Since ∠XYQ = ∠XYZ + ∠ZYQ
=> ∠XYQ = 64° + ∠QYP [ given ∠XYZ = 64° and ∠ZYQ = ∠QYP]
=> ∠XYQ =64° + 58° = 122°
Thus, ∠XYQ = 122° and Reflex ∠QYP = 302°