问题1.在给定图中,找到x和y的值,然后证明AB ||光盘。

解决方案:
After given names to the remaining vertices we get,

Now, Given ∠AEP = 50°, ∠CFQ = 130°
=> ∠EFD = ∠CFQ [vertically opposite angles are equal]
=> y = 130° [Given ∠CFQ = 130°]
=> y = 130° —eq(i)
Now, PQ is taking as straight line so, sum of all angles made on it is 180°
=> ∠AEP + ∠AEQ = 180°
=> 50° + x = 180°
=> x = 180° – 50° = 130°
=> x = 130° –eq(ii)
Now, from eq(i) and eq(ii) We conclude that x = y
As they are pair of alternate interior angles
So, AB || CD
Hence proved!!!
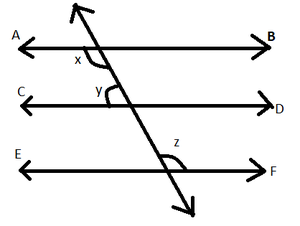
问题2.在给定图中,如果AB || CD,CD || EF和y:z = 3:7,找到x。
解决方案:
Given AB || CD and CD || EF y : z = 3 : 7
=> AB || CD || EF
=> AB || EF
So, x=z [alternate interior angles] –eq(i)
Again AB || CD
=> x + y = 180° [Co-interior angles]
=> z + y = 180° –eq(ii) [from eq(i)]
But given that y : z = 3 : 7
=> z = (7/3) y = (7/3)(180° – z) [from eq(ii)]
=> 10z = 7 * 180°
=> z = (7 * 180°)/10 =126°
=> z = 126° –eq(iii)
from eq(i) and eq(iii) we have
=> x = 126°
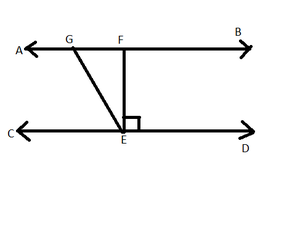
问题3.在给定图中,如果AB || CD,EF⊥CD和∠GED= 126°,找到∠AGE,∠GEF和∠FGE。
解决方案:
Given AB || CD, EF ⊥ CD, ∠GED = 126° and ∠FED =90°
=> ∠GED = ∠GEF + ∠FED
=> 126° = ∠GEF + 90° [Given]
=> ∠GEF = 36°
As, AB || CD and GE is a transversal
So, ∠FGE + ∠GED = 180° [ sum of Co- interior angles is 180 ]
=> ∠FGE + 126° = 180° [ Given ]
=> ∠FGE = 54°
As, AB || CD and GE is a transversal
So, ∠AGE = ∠GED [ alternate angles are equal ]
=> ∠AGE = 126°
问题4.在给定图中,如果PQ || ST,∠PQR= 110°,∠RST= 130°,找到∠QRS。
[提示:通过点R画一条与ST平行的线。]

解决方案:
Firstly we have drawn a line EF parallel to ST (EF || ST)
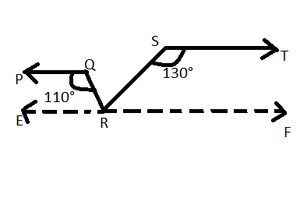
Since, PQ || ST [Given] and EF || ST [ Construction ]
So, PQ || EF and QR is a transversal
=> ∠PQR = ∠QRF [ Alternate interor angles ]
=> ∠QRF = 110° [Given ∠PQR =110° ]
=> ∠QRF = ∠QRS + ∠SRF
=> ∠QRS + ∠SRF = 110° –eq(i)
Again ST || EF and RS is a transversal
=>∠RST + ∠SRF = 180° [ sum of Co-interior angles is 180° ]
=>130° + ∠SRF =180° [Given]
=>∠SRF =50°
Now , from eq(i)
=> ∠QRS + ∠SRF = 110°
=> ∠QRS +50 = 110°
=> Thus, ∠QRS = 60°
问题5.在图6.32中,如果AB || CD,∠APQ = 50°,∠PRD = 127°,求x和y。

解决方案:
Given AB || CD and PQ is a transversal
=> ∠APQ = ∠PQR [ Alternate interior angles ]
=> x= 50° [ Given ∠APQ = 50° ]
=> x = 50°
Again, AB || CD and PR is a transversal
=>∠APR = ∠PRD [ Alternate interior angles ]
=> ∠APR = 127° [ Given ∠PRD = 127° ]
=> 50° + y =127° [Given ∠APQ = 50° ]
=> y =127° – 50° = 77°
=> y = 77°
Thus, x = 50° and y = 77°
问题6.在给定的图中,PQ和RS是彼此平行放置的两个反射镜。入射光线AB在B处入射到反射镜PQ,反射光线沿路径BC移动并在C处入射到反射镜RS,然后再次沿CD反射回来。证明AB ||光盘。

解决方案:
Draw ray BL ⊥ PQ and CM ⊥ RS
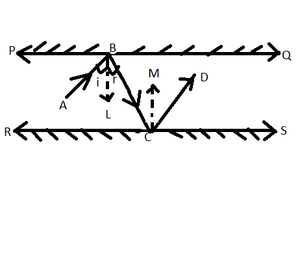
Since, PQ || RS => BL || CM
=>[ So, BL || PQ and CM || RS ]
Now, BL || CM and BC is a transversal
=> ∠LBC = ∠MCB –eq(i) [ Alternate interior angles ]
Since, angle of incidence = angle of reflection
=> ∠ABL = ∠LBC and ∠MCB = ∠MCD
=> ∠ABL = ∠MCD –eq(ii) [By eq(i)]
=>Adding eq(i) and eq(ii) we get
=> ∠LBC + ∠ABL = ∠MCB + ∠MCD
=> ∠ABC = ∠BCD
i.e, a pair of alternate angles are equal
Thus, AB || CD
Hence, Proved !!!