问题1. ABCD是一个四边形,其中P,Q,R和S是AB,BC,CD和DA边的中点(见图8.29)。 AC是对角线。显示:
(i)SR || AC和SR =½AC
(ii)PQ = SR
(iii)PQRS是平行四边形

解决方案:
Given that, P, Q, R and S are the mid points of quadrilateral ABCD
Theorem 8.9: The line segment joining the mid-points of two sides of a triangle is parallel to the third side.
(i) So here, taking ∆ACD
we can see S and R are the mid points of side AD and DC respectively. [Given]
Hence, SR || AC and SR = ½ AC (NCERT Theorem 8.9)……………………….(1)
(ii) So here, taking ∆ACB
we can see P and Q are the mid points of side AB and BC respectively. [Given]
Hence, PQ || AC and PQ = ½ AC (NCERT Theorem 8.9)…………………………(2)
From (1) and (2) we can say,
PQ = SR
(iii) so from (i) and (ii) we can say that
PQ || AC and SR || AC
so, PQ || SR and PQ = SR
If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
Hence, PQRS is a parallelogram.
问题2:ABCD是菱形,P,Q,R和S分别是AB,BC,CD和DA边的中点。证明四边形PQRS是一个矩形。
解决方案:
Given that, P, Q, R and S are the mid points of Rhombus ABCD.
Theorem 8.9: The line segment joining the mid-points of two sides of a triangle is parallel to the third side.
Construction: Join AC and BD

So here, taking ∆ABD
We can see P and S are the mid points of side AB and AD respectively. [Given]
Hence, PS || BD and PS = ½ BD (NCERT Theorem 8.9)……………………….(1)
Similarly, is we take ∆CBD
We can see R and Q are the mid points of side CD and CB respectively. [Given]
Hence, RQ || BD and RQ = ½ BD (NCERT Theorem 8.9)……………………….(2)
So from (1) and (2), we conclude that
PS || RQ and PS = RQ
If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
Hence, PQRS is a parallelogram.
Now in ∆ACD
We can see S and R are the mid points of side AD and CD respectively. [Given]
Hence, SR || AC and RS = ½ AC (NCERT Theorem 8.9)
from (2) RQ || BD and RQ = ½ BD (NCERT Theorem 8.9)
Hence, OGSH is a parallelogram.
∠HOG = 90° (Diagonal of rhombus intersect at 90°)
So ∠HSG = 90° (opposite angle of a parallelogram are equal)
As, PQRS is a parallelogram having vertices angles equal to 90°.
Hence, PQRS is a Rectangle.
问题3. ABCD是一个矩形,P,Q,R和S分别是边AB,BC,CD和DA的中点。证明四边形PQRS是菱形。
解决方案:
Given that, P, Q, R and S are the mid points of Rectangle ABCD.
Construction: Join AC
Theorem 8.9 : The line segment joining the mid-points of two sides of a triangle is parallel to the third side.

So here, taking ∆ACD
we can see S and R are the mid points of side AD and DC respectively. [Given]
Hence, SR || AC and SR = ½ AC (NCERT Theorem 8.9)……………………….(1)
Now, taking ∆ACB
we can see P and Q are the mid points of side AB and BC respectively. [Given]
Hence, PQ || AC and PQ = ½ AC (NCERT Theorem 8.9)…………………………(2)
So from (1) and (2), we conclude that
SR || PQ and SR = PQ
Hence, PQRS is a parallelogram. (If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram)
Now in ∆QBP and ∆QCR
QC = QB (Q is the mid point of BC)
RC = PB (opposite sides are equal, hence half length is also equal)
∠QCR = ∠QBP (Each 90°)
∆QBP ≅ ∆QCR (By SAS congruency)
QR = QP (By C.P.C.T.)
As PQRS is a parallelogram and having adjacent sides equal
Hence, PQRS is a rhombus
问题4. ABCD是一个梯形,其中AB || DC,BD是对角线,E是AD的中点。穿过E线平行于AB并在F处与BC相交(见图8.30)。证明F是BC的中点。

解决方案:
Let O be the point of intersection of lines BD and EF
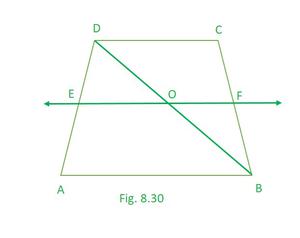
Theorem 8.10 : The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.
So here, taking ∆ADB
we can see S is the mid point of side AD and ED || AB [Given]
Hence, OD = ½ BD ………..(NCERT Theorem 8.10)
Now, taking ∆BCD
we can see O is the mid point of side BD and OF || AB [Proved and Given]
Hence, CF = ½ BC…….. (NCERT Theorem 8.10)
Hence proved!!
问题5.在平行四边形ABCD中,E和F分别是边AB和CD的中点(见图8.31)。证明线段AF和EC将对角线BD一分为三。

解决方案:
Theorem 8.10 : The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.
Given, E and F are the mid points of side AB and CD of parallelogram ABCD.
As, AB || CD and AB = CD (opposite sides of parallelogram)………..(1)
AE = CF (halves of opposite sides of parallelogram)………………………(2)
from (1) and (2)
AECF is a parallelogram
Hence, AF || EC
Now taking ∆APB
we can see E is the mid point of side AB and EF || AP [Given and proved]
Hence, BQ = PQ………..(NCERT Theorem 8.10)………………….(1)
Now taking ∆CQD
we can see F is the mid point of side CD and CQ || FP [Given and proved]
Hene, DP = PQ………..(NCERT Theorem 8.10)………………..(2)
From (1) and (2) we conclude that,
BQ = PQ = DQ
Hence, we can say that line segments AF and EC trisect the diagonal BD
问题6:证明连接四边形的相对边的中点的线段彼此一分为二。
解决方案:
Theorem 8.9 : The line segment joining the mid-points of two sides of a triangle is parallel to the third side.

So here, taking ∆ACD
we can see S and R are the mid points of side AD and DC respectively. [Given]
Hence, SR || AC and SR = ½ AC (NCERT Theorem 8.9)……………………….(1)
Now, taking ∆ACB
we can see P and Q are the mid points of side AB and BC respectively. [Given]
Hence, PQ || AC and PQ = ½ AC (NCERT Theorem 8.9)…………………………(2)
So from (1) and (2), we conclude that
SR || PQ and SR = PQ
Hence, PQRS is a parallelogram. (If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram)
And since the diagonal of parallelogram bisects each other
so, QS and PR bisects each other.
问题7. ABC是与C成直角的三角形。穿过斜边AB的中点M并平行于BC的线在D处与AC相交。
(i)D是AC的中点
(ii)MD⊥AC
(iii)CM = MA =½AB
解决方案:
Theorem 8.10 : The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.

(i) while taking ∆ABC
we can see M is the mid point of side AB and DM || BC [Given]
This implies, DC= AD ……….. (NCERT Theorem 8.10)
Hence, D is the mid-point of AC.
(ii) As we know MD || BC and AC is transversal
This implies, ∠ACB = ∠ADM = 90°
Hence, MD ⊥AC
(iii) Considering ∆ADM and ∆CDM
AD = CD (D is the mid point of AC (Proved))
∠CDM = ∠ADM (proved, MD ⊥AC)
DM = DM (common)
∆ADM ≅ ∆CDM (By SAS congruency)
CM = AM (By C.P.C.T.)
CM = AM = ½ AB (M is the mid point of AB)