问题1.在下图中找到x。
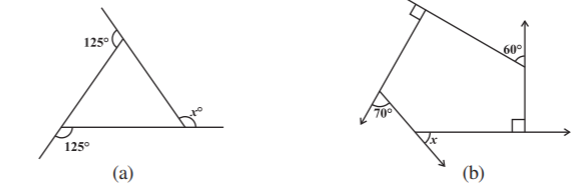
解决方案:
As we know , the sum of the measures of the external angles of any polygon is 360°.
(a) 125° + 125° + x = 360° ⇒ 250° + x = 360° ⇒ x = 110°
(a) 70° + 60° + x + 90° + 90° = 360° ⇒ 310° + x = 360° ⇒ x = 50°
问题2。找到正则多边形的每个外角的度量
(i)9面
解决方案:
Measure of angles = 360°/ 9 = 40°
As in a regular polygon all interior angle are equal so all the exterior angles will also be equal.
(ii)15面
解决方案:
Measure of angles = 360°/ 15 = 24°
问题3.如果外角的大小为24°,则正多边形有多少个边?
解决方案:
Given measure of exterior angle = 24°
(no. of sides) x (measure of exterior angle) = 360° ⇒ no. of sides = 360°/24° = 15
问题4.如果一个规则多边形的每个内角均为165°,则它们具有多少个边?
解决方案:
Given measure of interior angle = 165°
measure of exterior angle = 180° – 165° = 15°
(no. of sides) x (measure of exterior angle) = 360° ⇒ no. of sides = 360°/15° = 24
问题5(a)是否可以有一个规则的多边形,每个外部角度的测量值为22°?
(b)它可以是正多边形的内角吗?为什么?
解决方案:
(a) given here, measure of exterior angle = 22°
As we know, (no. of sides) x (measure of exterior angle) = 360°
putting here value, we get
No. of sides = 360°/22° ≈ 16.36 (approx), which is never possible .
Number of sides can never be fractional.
(b) No. It cannot be an interior angle of a regular polygon.
In this case , measure of exterior angle will be = 158°
again we will get fractional no. of sides. Hence not possible.
问题6.(a)规则多边形的最小内角是多少?为什么?
(b)规则多边形最大可能的外角是多少?
解决方案:
(a) An Equilateral Triangle is a regular polygon with minimum number of sides because all sides are equal in it. We know that each angle of an equilateral triangle measures 60° . Hence, 60° is the minimum possible value for internal angle of a regular polygon.
(b) Each exterior angle of an equilateral triangle is 120° and hence this the maximum possible value of exterior angle of a regular polygon. This can also be proved by another principle; which states that each exterior angle of a regular polygon is equal to 360° divided by number of sides in the polygon. If 360° is divided by 3, we get 120° .