9类NCERT解决方案-第4章包含两个变量的线性方程-练习4.3

问题1.在两个变量中绘制以下每个线性方程式的图形：

(i)x + y = 4

(ii)x – y = 2

(iii)y = 3倍

(iv)3 = 2x + y

解决方案：

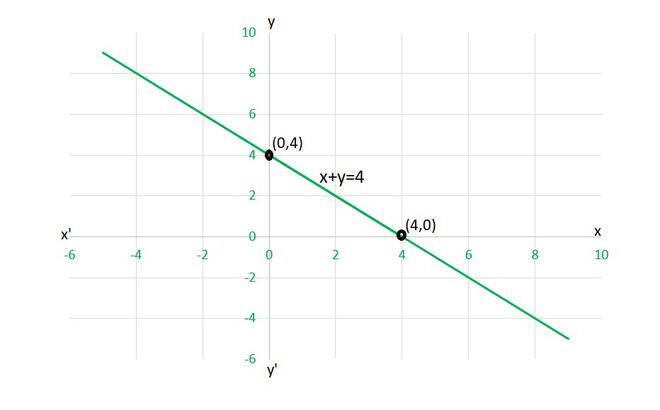
(i) To draw the graph x+y=4, we need at least two solutions of the equation. 

We can check that when, x = 0, y = 4, 

and x = 4, y = 0 

are solutions of the given equation. So, we can use the following table to draw the graph:

x	y
0	4
4	0

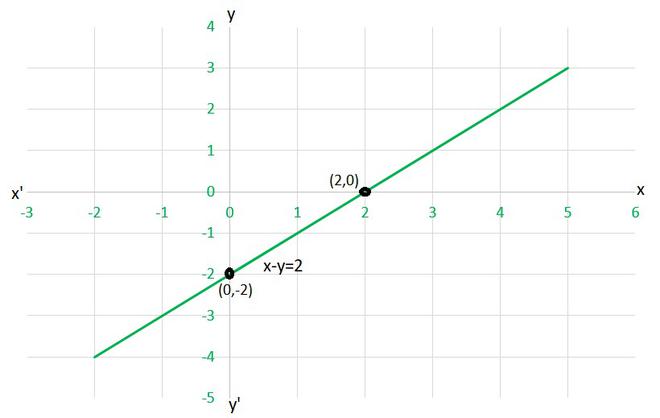
(ii) To draw the graph x-y=2, we need at least two solutions of the equation.

We can check that when, x = 0, y = -2,

and x = 2, y = 0

are solutions of the given equation. So, we can use the following table to draw the graph:

x	y
0	-2
2	0

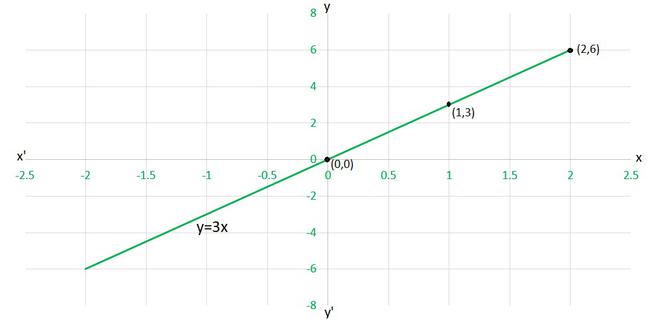
(iii) To draw the graph y=3x, we need at least two solutions of the equation.

We can check that when, x = 0, y =0,

and x = 1, y = 3

are solutions of the given equation. So, we can use the following table to draw the graph :

x	y
0	0
1	3

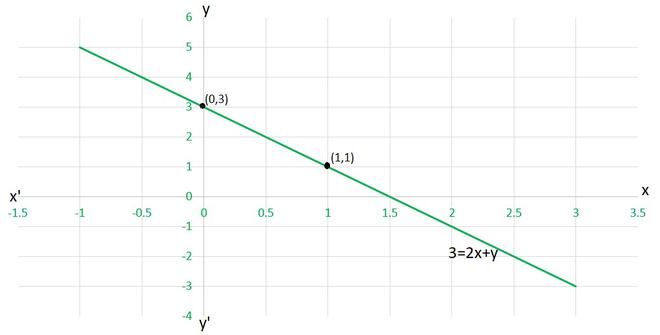
(iv) To draw the graph 3=2x+y, we need at least two solutions of the equation.

We can check that when, x = 0, y =3,

and x = 1, y = 1

are solutions of the given equation. So, we can use the following table to draw the graph :

x	y
0	3
1	1

问题2.给出通过(2，14)的两条直线的方程式。那里还有几条这样的线，为什么呢?

解决方案：

Here, as given point is (2,14) so

x=2 and y=14

We can form various equation such as,

y-x = 14-2 = 12

x+y = 2+14 =16

2x+y = 4+14 = 18

y-2x = 14-4 = 10

y = 14

x = 2

and many more……..

In fact, there are infinitely many linear equations which are satisfied by the coordinates of the point (2, 14).

As it is stated that there can be infinite lines passing through a point. So here,

⟹

问题3.如果点(3，4)位于等式3y = ax + 7的图形上，请找到a的值。

解决方案：

The given equation is

3y = ax+7

According to the given point (3,4), 

x = 3 and y = 4

As this point lie on this graph, then it will satisfy these points. So substituting the values 

3y = ax+7

⟹ (3×4) = (a×3)+7

12 = 3a+7

 3a = 12–7

3a = 5

a = $\frac{5}{3}$

Hence, the value of a = $\frac{5}{3}$.

问题4.在城市中的出租车费如下：第一个公里的车费为₹8，随后的距离为每公里₹5。以覆盖的距离为x km，总票价为₹y，为此信息编写一个线性方程式，并绘制其图。

解决方案：

So, as given in the question, we will take 

Distance covered as x km 

and total fare as ₹ y

Fare for the first kilometer = 8 per km

Fare after the first 1km = ₹ 5 per km

Let x is the total distance, then the distance after one km will be = (x-1)km

Hence., Fare after the first km = 5(x-1)

So, in equation form we can conclude that, 

The total fare = Fare of first km+ fare after the first km

y = 8+5(x-1)

y = 8+5(x-1)

y = 8+5x – 5

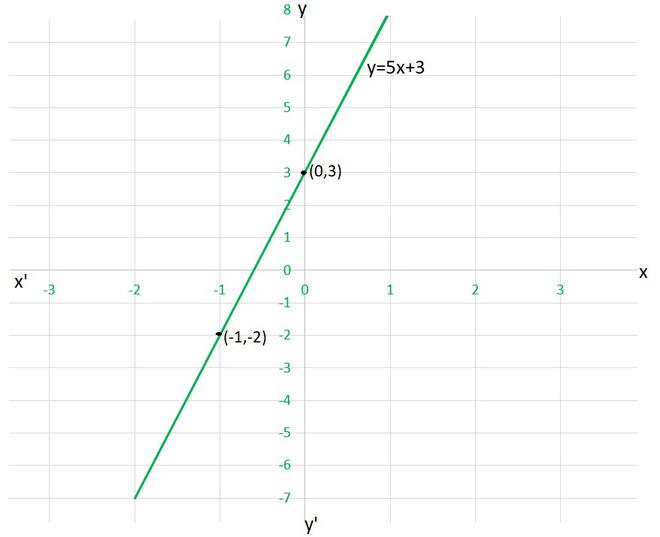
y = 5x+3

To draw the graph y=5x+3, we need at least two solutions of the equation.

We can check that when, x = 0, y =3,

and x = -1, y = -2

are solutions of the given equation. So, we can use the following table to draw the graph :

x	y
0	3
-1	-2

问题5.从下面给出的选择中，选择方程，其图在图4.6和图4.7中给出。

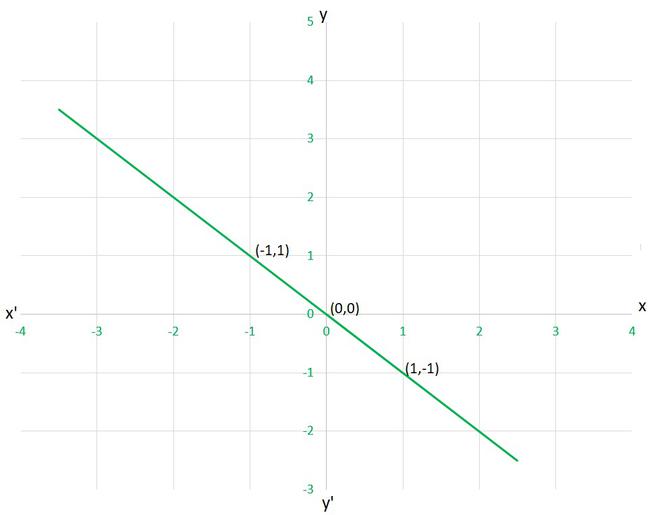
对于图4。6

(i)y = x

(ii)x + y = 0

(iii)y = 2x

(iv)2 + 3y = 7x

解决方案：

Let’s check each given cases, whether they are satisfying the solution given on graph or not,

(i) y=x

as given point  (1,-1)

x=1 and y=-1 ⟹ x≠y

Hence, this equation is INCORRECT for this graph.

(ii) x+y=0

as given point (1,-1), (1,-1) and (0,0)

x=1 and y=-1 ⟹ x+y=0

x=-1 and y=1 ⟹ x+y=0

x=0 and y=0 ⟹ x+y=0

Hence, this equation is CORRECT for this graph.

(iii) y=2x

as given point  (1,-1)

x=1 and y=-1 ⟹ y≠2x

Hence, this equation is INCORRECT for this graph.

(iii) 2+3y=7x

as given point  (1,-1)

x=1 and y=-1 ⟹ 2+3y≠7x

Hence, this equation is INCORRECT for this graph.

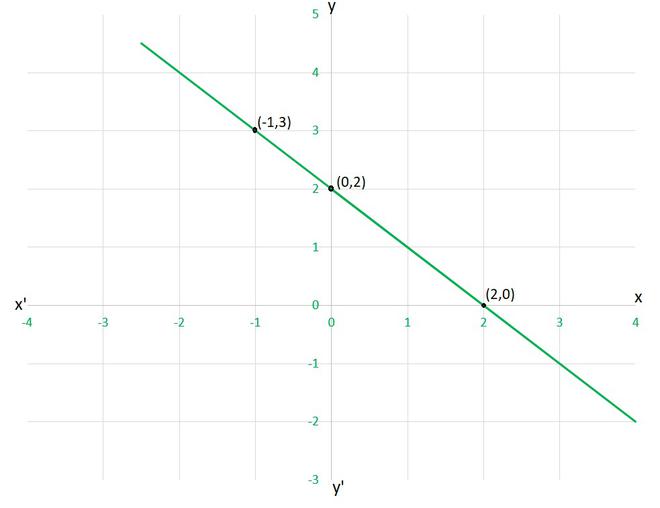
对于图4.7

(i)y = x + 2

(ii)y = x – 2

(iii)y = –x + 2

(iv)x + 2y = 6

解决方案：

Let’s check each given cases, whether they are satisfying the solution given on graph or not,

(i) y=x+2

as given point (0,2), (2,0) and (-1,3)

x=0 and y=2 ⟹ y=x+2

x=2 and y=0 ⟹ y≠x+2

Hence, this equation is INCORRECT for this graph.

(ii) y=x-2

as given point (0,2)

x=0 and y=2 ⟹ y≠x-2

Hence, this equation is INCORRECT for this graph.

(iii) y=-x+2

as given point (0,2)

x=0 and y=2 ⟹ y=-x+2

x=2 and y=0 ⟹ y=-x+2

x=-1 and y=3 ⟹ y=-x+2

Hence, this equation is CORRECT for this graph.

(iii) x+2y=6

as given point (0,2)

x=0 and y=2 ⟹ x+2y≠6

Hence, this equation is INCORRECT for this graph.

问题6：如果物体在施加恒定力时所做的功与该物体行进的距离成正比，则以方程形式将其表示为两个变量，并通过施加恒定力来绘制该物体的图形5个单位还可以从图中读取到人体行进距离为

(i)2个单位

(ii)0个单位

解决方案：

Given in question,

Work done = force × displacement

where constant force = 5 units

lets take work done as y units

and, distance travelled by the body x units

Hence, the equation can be expressed as,

y=5x

To draw the graph y=5x, we need at least two solutions of the equation.

We can check that when, x = 0, y =0,

and x = 1, y = 5

are solutions of the given equation. So, we can use the following table to draw the graph :

x	y
0	0
1	5

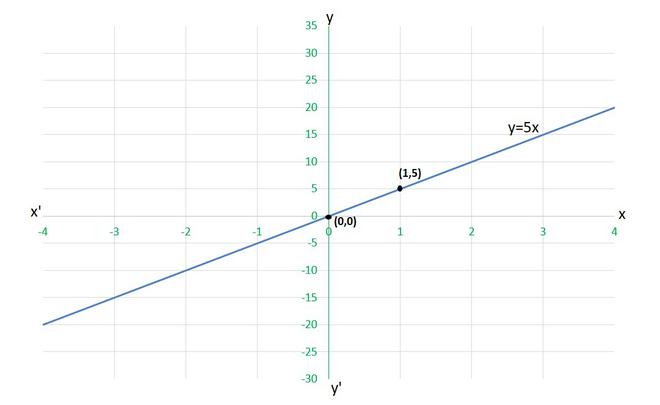
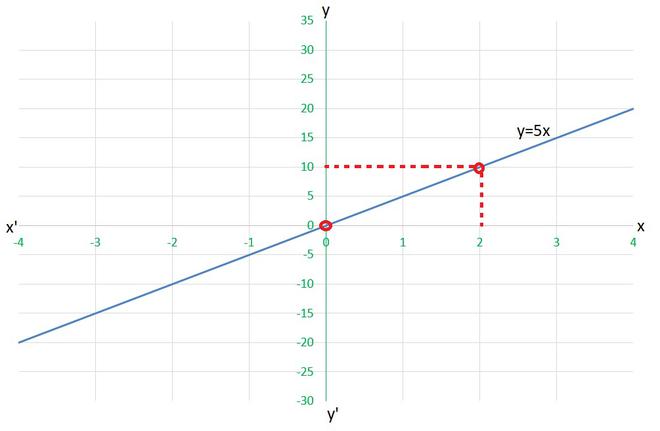
(i) for x= 2 units

y=5×2

work done = 10 units

(ii) for x= 0 units

y=5×0

work done = 0 units

问题7：Yamini和Fatima，这是一所学校IX级的两名学生，共同向总理救济基金捐款100卢比，以帮助地震灾民。编写一个满足该数据的线性方程。 (您可以将他们的缴费记为₹x和₹y)。绘制相同的图形。

解决方案：

Let’s take Yamini’s contribution as ₹ x and Fatima’s contribution as ₹ y.

As they together contributed ₹ 100, so the equation can be formed as,

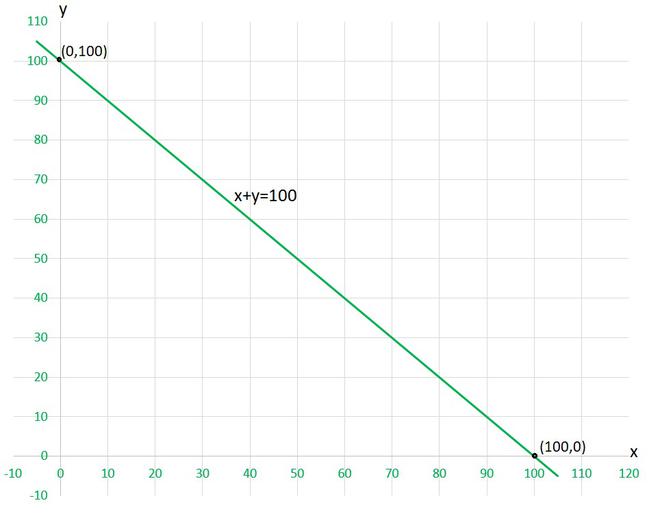
x+y=100

To draw the graph x+y=100, we need at least two solutions of the equation.

We can check that when, x = 0, y =100,

and x = 100, y = 0

are solutions of the given equation. So, we can use the following table to draw the graph :

x	y
0	100
100	0

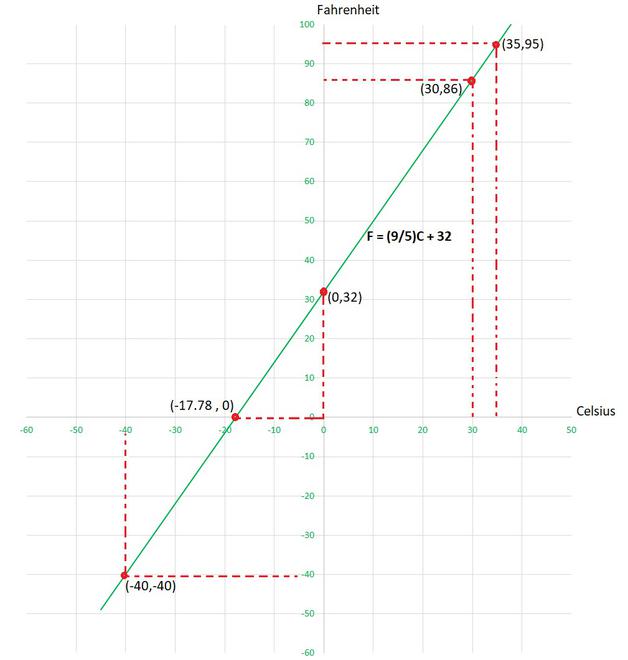
问题8.在美国和加拿大等国家/地区，温度以华氏度为单位，而在印度等国家/地区，以摄氏度为单位。这是将华氏温度转换为摄氏温度的线性方程式：

F = $\mathbf{\frac{9}{5}}$ C + 32

(i)使用摄氏温度x轴和华氏温度y轴绘制上述线性方程式的图形。

(ii)如果温度为30°C，华氏温度是多少?

(iii)如果温度为95°F，摄氏温度是多少?

(iv)如果温度为0°C，华氏温度是多少?如果温度是0°F，摄氏温度是多少?

(v)华氏温度和摄氏温度在数值上是否相同?如果是，找到它。

解决方案：

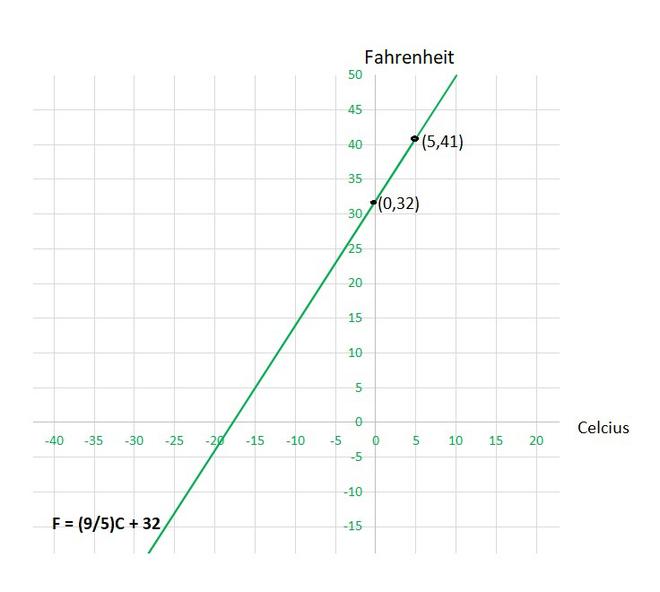
(i) Taking Celsius on x-axis and Fahrenheit on y-axis , so equation will be as follows:

y = $\frac{9}{5}$x + 32

To draw the graph y = $\frac{9}{5}$x + 32, we need at least two solutions of the equation.

We can check that when, x = 0, y =32,

and x = 5, y = 41

are solutions of the given equation. So, we can use the following table to draw the graph :

x	y
0	32
5	41

(ii) When the temperature is 30°C then, using the equation

y = $\frac{9}{5}$x + 32

by substituting, x=30, we get

y = $\frac{9}{5}$×30 + 32

y = 86 

Hence, in Fahrenheit temperature will be 86°F

(iii) When the temperature is 95°F then, using the equation

y = $\frac{9}{5}$x + 32

by substituting, y=95, we get

95 = $\frac{9}{5}$x+ 32

x = $\frac{(95-32)×5}{9}$

x = 35

Hence, in Celsius temperature will be 35°C

(iv)When the temperature is 0°C, using the equation

y = $\frac{9}{5}$x + 32

by substituting, x=0, we get

y = $\frac{9}{5}$×0 + 32

y = 32

Hence, in Fahrenheit temperature will be 32°F

and, when the temperature is 0°F, using the equation and by substituting, y=0, we get

0 = $\frac{9}{5}$x + 32

x = $\frac{(-32)×5}{9}$

x = -17.78

Hence, in Celsius temperature will be -17.78°C.

(v) Lets take both temperature same as x.

so, equation becomes as follows:

x = $\frac{9}{5}$x + 32

$\frac{9}{5}$x-x = -32

$\frac{4}{5}$x = -32

x = -32×$\frac{4}{5}$

x = -40

Hence, Celsius and Fahrenheit temperature will be -40°C and -40°F respectively.