10类NCERT解决方案-第3章两个变量的线性方程对–练习3.2

问题1.在以下问题中形成一对线性方程，并以图形方式找到其解。

(i)X级的10名学生参加了数学测验。如果女孩的数量比男孩的数量多4，请找到参加测验的男孩和女孩的数量。

解决方案：

Let’s take,

Number of girls = x

Number of boys = y

According to the given conditions,

x + y = 10            -(1)

x – y = 4             -(2)

So, to construct a graph, we need to find at least two solutions of the given equation.  

For equation (1)

x + y = 10, So, we can use the following table to draw the graph:

x	y
0	10
10	0

For equation (2)

x – y = 4, So, we can use the following table to draw the graph:

x	y
0	-4
4	0

The graph will be as follows for Equation (1) and (2):

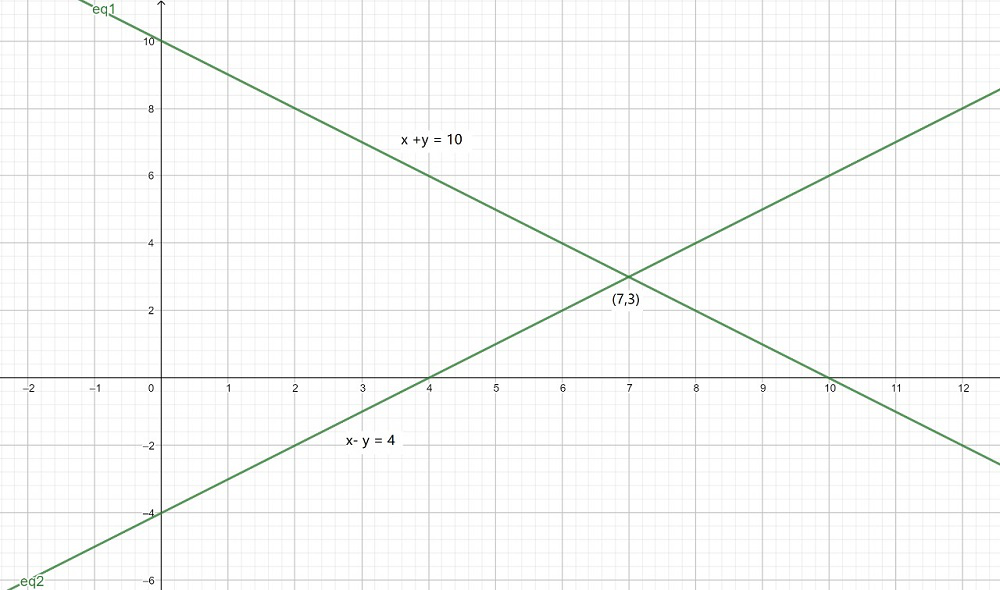
Now, from the graph, we can conclude the given lines intersect each other at point (7, 3).

Hence, the number of girls are 7 and number of boys are 3 in a class.

(ii)5支铅笔和7支钢笔合计₹50，而7支铅笔和5支钢笔合计₹46。找到一支铅笔和一支笔的成本。

解决方案：

Let’s take,

Cost for one pencil = x

Cost for one pencil = y

According to the given conditions,

5x + 7y = 50             -(1)

7x + 5y = 46             -(2)

So, to construct a graph, we need to find at least two solutions of the given equation.  

For equation (1)

5x + 7y = 50, So, we can use the following table to draw the graph:

x	y
3	5
10	0

For equation (2)

7x + 5y = 46, So, we can use the following table to draw the graph:

x	y
3	5
8	-2

The graph will be as follows for Equation (1) and (2):

Now, from the graph, we can conclude the given lines intersect each other at point (3, 5).

Hence, the cost of a pencil is ₹ 3 and cost of a pen is ₹ 5.

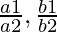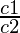问题2.比较比率$\frac{a1}{a2}, \frac{b1}{b2}$ ， 和$\frac{c1}{c2}$ ，找出代表以下线性方程对的线在一个点处相交，平行或重合：

(i)5x – 4y + 8 = 0； 7x + 6y – 9 = 0

解决方案：

In the given equations, 

a1 = 5

a2 = 7

b1 = -4

b2 = 6

c1 = 8

c2 = -9

Now, here

a1/a2 = 5/7

b1/b2 = -4/6 = -2/3

c1/c2 = 8/-9

As, here

$\frac{a1}{a2} ≠ \frac{b1}{b2}$

Hence, the given pairs of equations have a unique solution and the lines intersect each other at exactly one point.

(ii)9x + 3y + 12 = 0； 18x + 6y + 24 = 0

解决方案：

In the given equations,

a1 = 9

a2 = 18

b1 = 3

b2 = 6

c1 = 12

c2 = 24

Now, here

a1/a2 = 9/18 = 1/2

b1/b2 = 3/6 = 1/2

c1/c2 = 12/24 = 1/2

As, here

$\frac{a1}{a2} = \frac{b1}{b2} = \frac{c1}{c2}$

Hence, the given pairs of equations have infinite many solutions and the lines are coincident.

(iii)6x – 3y + 10 = 0； 2x – y + 9 = 0

解决方案：

In the given equations,

a1 = 6

a2 = 2

b1 = -3

b2 = -1

c1 = 10

c2 = 9

Now, here

a1/a2 = 6/2 = 3

b1/b2 = -3/-1 = 3

c1/c2 = 10/9

As, here

$\frac{a1}{a2} = \frac{b1}{b2} ≠ \frac{c1}{c2}$

Hence, the given pairs of equations have no solution and the lines are parallel and never intersect each other.

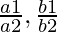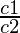问题3.关于比率的比较$\frac{a1}{a2}, \frac{b1}{b2}$ ， 和$\frac{c1}{c2}$ ，找出下面的线性方程对是一致的还是不一致的。

(i)3x + 2y = 5； 2x – 3y = 7

解决方案：

In the given equations,

a1 = 3

a2 = 2

b1 = 2

b2 = -3

c1 = -5

c2 = -7

Now, here

a1/a2 = 3/2

b1/b2 = 2/-3

c1/c2 = -5/-7

As, here

$\frac{a1}{a2} ≠ \frac{b1}{b2}$

Hence, the given pairs of equations have a unique solution and the lines intersect each other at exactly one point.

Pair of linear equations are CONSISTENT.

(ii)2x – 3y = 8； 4x – 6y = 9

解决方案：

In the given equations,

a1 = 2

a2 = 4

b1 = -3

b2 = -6

c1 = -8

c2 = -9

Now, here

a1/a2 = 2/4 = 1/2

b1/b2 = -3/-6 = 1/2

c1/c2 = -8/-9 = 8/9

As, here

$\frac{a1}{a2} = \frac{b1}{b2} ≠ \frac{c1}{c2}$

Hence, the given pairs of equations have no solution and the lines are parallel and never intersect each other.

Pair of linear equations are INCONSISTENT.

(iii) 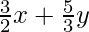$\frac{3}{2}x + \frac{5}{3}y$ = 7; 9x – 10y = 14

解决方案：

In the given equations,

a1 = 3/2 

a2 = 9

b1 = 5/3 

b2 = -10

c1 = -7

c2 = -14

Now, here

$\frac{a1}{a2} = \frac{\frac{3}{2}}{9} = \frac{1}{6}$

$\frac{b1}{b2} = \frac{\frac{5}{3}}{-10} = \frac{-1}{6}$

c1/c2 = -7/-14 = 1/2

As, here

$\frac{a1}{a2} ≠ \frac{b1}{b2}$

Hence, the given pairs of equations have a unique solution and the lines intersect each other at exactly one point.

Pair of linear equations are CONSISTENT.

(iv)5x – 3y = 11； – 10x + 6y = –22

解决方案：

In the given equations,

a1 = 5

a2 = -10

b1 = -3

b2 = 6

c1 = -11

c2 = 22

Now, here

a1/a2 = 5/-10 = -1/2

b1/b2 = -3/6 = -1/2

c1/c2 = -11/22 = -1/2

As, here

$\frac{a1}{a2} = \frac{b1}{b2} = \frac{c1}{c2}$

Hence, the given pairs of equations have infinite many solutions and the lines are coincident.

Pair of linear equations are CONSISTENT.

(v) 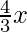$\frac{4}{3}x$ + 2y = 8; 2x + 3y = 12

解决方案：

In the given equations,

a1 = 4/3 

a2 = 2

b1 = 2

b2 = 3

c1 = -8

c2 = -12

Now, here

$\frac{a1}{a2} = \frac{\frac{4}{3} }{2} = \frac{2}{3}$

b1/b2 = 2/3

c1/c2 = -8/-12 = 2/3

As, here

$\frac{a1}{a2} = \frac{b1}{b2} = \frac{c1}{c2}$

Hence, the given pairs of equations have infinite many solutions and the lines are coincident.

Pair of linear equations are CONSISTENT.

问题4.以下哪些线性方程对是一致/不一致的?如果一致，请以图形方式获取解决方案：

(i)x + y = 5，2x + 2y = 10

解决方案：

In the given equations,

a1 = 1

a2 = 2

b1 = 1

b2 = 2

c1 = -5

c2 = -10

Now, here

a1/a2 = 1/2

b1/b2 = 1/2

c1/c2 = -5/-10 = 1/2

As, here

$\frac{a1}{a2} = \frac{b1}{b2} = \frac{c1}{c2}$

Hence, the given pairs of equations have infinite many solutions and the lines are coincident.

Pair of linear equations are CONSISTENT.

x + y = 5             -(1)

2x + 2y = 10             -(2)

So, to construct a graph, we need to find at least two solutions of the given equation.  

For equation (1)

x + y = 5, So, we can use the following table to draw the graph:

x	y
0	5
5	0

For equation (2)

2x + 2y = 10, So, we can use the following table to draw the graph:

x	y
0	5
5	0

The graph will be as follows for Equation (1) and (2):

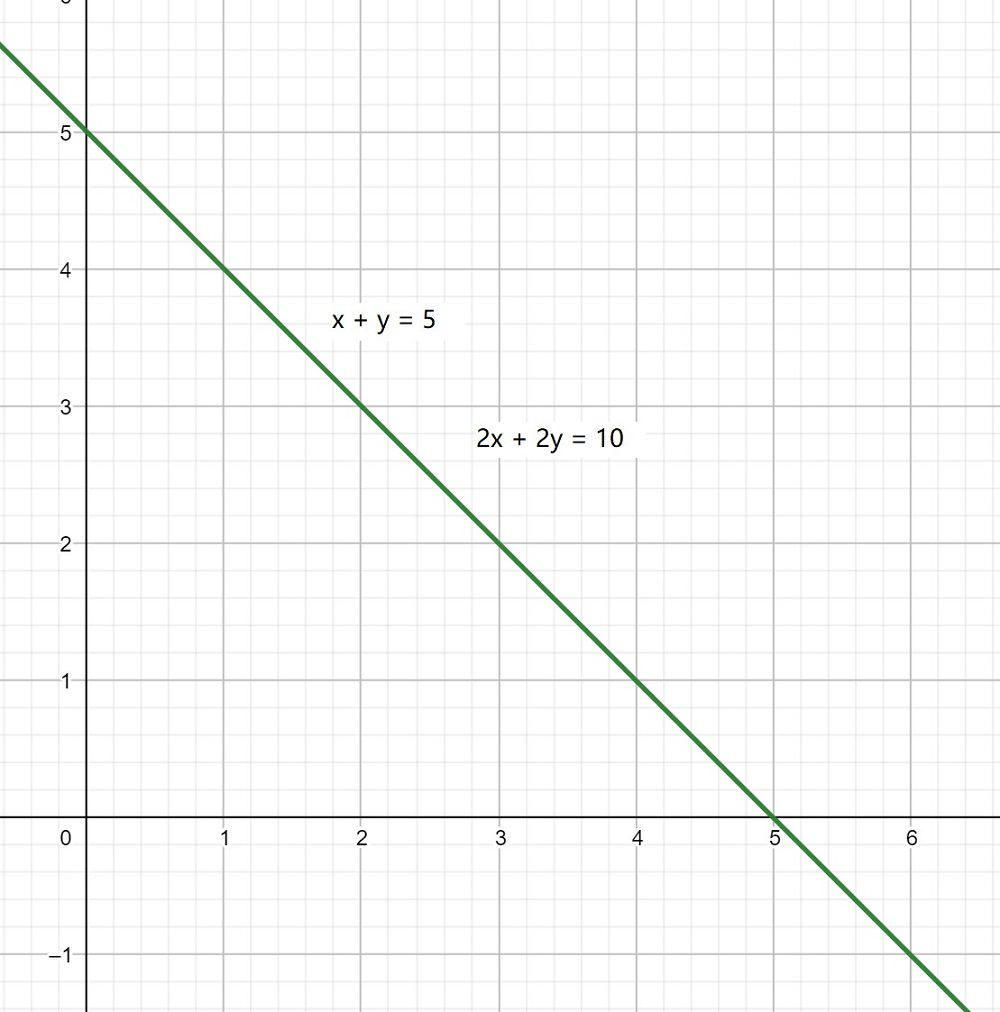
(ii)x – y = 8，3x – 3y = 16

解决方案：

In the given equations,

a1 = 1

a2 = 3

b1 = -1

b2 = -3

c1 = -8

c2 = -16

Now, here

a1/a2 = 1/3

b1/b2 = 1/3

c1/c2 = -8/-16 = 1/2

As, here

$\frac{a1}{a2} = \frac{b1}{b2} ≠ \frac{c1}{c2}$

Hence, the given pairs of equations have no solution and the lines are parallel and never intersect each other.

Pair of linear equations are INCONSISTENT.

(iii)2x + y – 6 = 0，4x – 2y – 4 = 0

解决方案：

In the given equations,

a1 = 2

a2 = 4

b1 = 1

b2 = -2

c1 = -6

c2 = -4

Now, here

a1/a2 = 2/4 = 1/2

b1/b2 = 1/-2

c1/c2 = -6/-4 = 3/2

As, here

$\frac{a1}{a2} ≠ \frac{b1}{b2}$

Hence, the given pairs of equations have a unique solution and the lines intersect each other at exactly one point.

Pair of linear equations are CONSISTENT.

2x + y – 6 = 0             -(1)

4x – 2y – 4 = 0              -(2)

So, to construct a graph, we need to find at least two solutions of the given equation.  

For equation (1)

2x + y – 6 = 0, So, we can use the following table to draw the graph:

x	y
0	6
3	0

For equation (2)

4x – 2y – 4 = 0, So, we can use the following table to draw the graph:

x	y
0	-2
1	0

The graph will be as follows for Equation (1) and (2):

Now, from the graph, we can conclude the given lines intersect each other at point (2, 2).

(iv)2x – 2y – 2 = 0，4x – 4y – 5 = 0

解决方案：

In the given equations,

a1 = 2

a2 = 4

b1 = -2

b2 = -4

c1 = -2

c2 = -5

Now, here

a1/a2 = 2/4 = 1/2

b1/b2 = -2/-4 = 1/2

c1/c2 = -2/-5 = 2/5

As, here

$\frac{a1}{a2} = \frac{b1}{b2} ≠ \frac{c1}{c2}$

Hence, the given pairs of equations have no solution and the lines are parallel and never intersect each other.

Pair of linear equations are INCONSISTENT.

问题5.矩形花园的周长的一半为36 m，该矩形花园的长度比其宽度大4 m。找到花园的尺寸。

解决方案：

Let’s take,

length = x

breadth = y

Half the perimeter of a rectangular garden = $\frac{2(x+y)}{2}$ = x + y

According to the given conditions,

x = y + 4             -(1)

x + y = 36              -(2)

So, to construct a graph, we need to find at least two solutions of the given equation.  

For equation (1)

x = y + 4, So, we can use the following table to draw the graph:

x	y
0	-4
4	0

For equation (2)

x + y = 36, So, we can use the following table to draw the graph:

x	y
0	36
36	0

The graph will be as follows for Equation (1) and (2):

Now, from the graph, we can conclude the given lines intersect each other at point (20, 16).

Hence, length is 20 m and breath is 16 m of rectangle.

问题6.给定线性方程2x + 3y – 8 = 0，在两个变量中编写另一个线性方程，以使如此形成的对的几何表示为：

(i)相交线

解决方案：

Linear equation in two variables such that pair so formed is intersecting lines, so it should satisfy the given conditions

$\frac{a1}{a2} ≠ \frac{b1}{b2}$

By rearranging, we get

$\frac{a1}{b1} ≠ \frac{a2}{b2}$

Hence, the required equation should not be in ratio of 2/3 

Hence, another equation can be 2x – 9y + 9 = 0

where the ratio is 2/-9 

and, $\frac{2}{3} ≠ \frac{2}{-9}$

(ii)平行线

解决方案：

Linear equation in two variables such that pair so formed is parallel lines, so it should satisfy the given conditions

$\frac{a1}{a2} = \frac{b1}{b2} ≠ \frac{c1}{c2}$

By rearranging, we get

$\frac{a1}{b1} = \frac{a2}{b2}$

$\frac{b1}{c1} ≠ \frac{b2}{c2}$

Hence, the required equation a2/b2 should be in ratio of 2/3 and b2/c2 should not be equal to 3/-8 

Hence, another equation can be 4x + 6y + 9 = 0

where the ratio a2/b2 is 2/3

and,$\frac{b2}{c2} ≠ \frac{3}{-8}$

(iii)重合线

解决方案：

Linear equation in two variables such that pair so formed is parallel lines, so it should satisfy the given conditions

$\frac{a1}{a2} = \frac{b1}{b2} = \frac{c1}{c2}$

By rearranging, we get

$\frac{a1}{b1} = \frac{a2}{b2}$

$\frac{b1}{c1} = \frac{b2}{c2}$

Hence, the required equation a2/b2 should be in ratio of 2/3 and b2/c2 should be equal to 3/-8 

Hence, another equation can be 4x + 6y -16 = 0

where the ratio a2/b2 is 2/3 

and, b2/c2 = 3/-8

问题7.绘制方程x – y + 1 = 0和3x + 2y – 12 = 0的图形。确定由这些线和x轴形成的三角形的顶点坐标，并为三角形区域加上阴影。

解决方案：

x – y + 1 = 0              -(1)

3x + 2y – 12 = 0              -(2)

So, to construct a graph, we need to find at least two solutions of the given equation.  

For equation (1)

x – y + 1 = 0, So, we can use the following table to draw the graph:

x	y
0	-1
1	0

For equation (2)

3x + 2y – 12 = 0, So, we can use the following table to draw the graph:

x	y
0	6
4	0

The graph will be as follows for Equation (1) and (2):

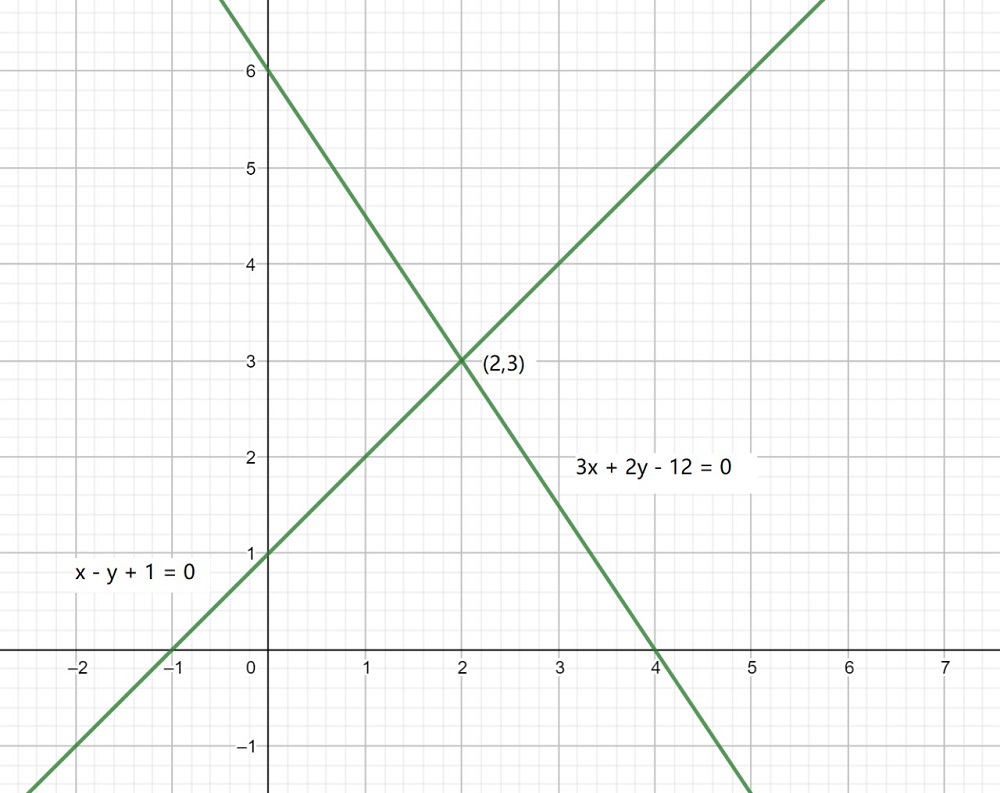
Now, from the graph, we can conclude the given lines intersect each other at point (2, 3), and x-axis at (−1, 0) and (4, 0). 

Hence, the vertices of the triangle are (2, 3), (−1, 0), and (4, 0).