问题1.通过将以下方程对简化为一对线性方程来求解它们:
(一世) 
解决方案:
Lets, take 1/x = a and 1/y = b
Here, the two given equation will be as follows:
![]() +
+ ![]() = 2
= 2
Multiply it by 6, we get
3a + 2b = 12 -(1)
and,
![]() +
+ ![]() =
= ![]()
Multiply it by 6, we get
2a + 3b = 13 -(2)
Now, by using Elimination method,
Multiply eq(1) by 2 and multiply eq(2) by 3, and then subtract them

5b = 15
b = 3
Now putting b = 3 in eq(1), we get
3a + 2(3) = 12
a = 6/3
a = 2
So, Now As
a = 1/x = 2
x = 1/2
b = 1/y = 3
y = 1/3
(ii) 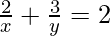
解决方案:
Lets, take 2/√x = a and 3/√y = b
Here, the two given equation will be as follows:
a + b = 2 -(1)
and,
2a – 3b =-1 -(2)
Now, by using Elimination method,
Multiply eq(1) by 3, and then add them

5a = 5
a = 1
Now putting a = 1 in eq(1), we get
1 + b = 2
b = 1
So, Now As
a = 2/√x = 1
√x = 2
x = 4
b = 3/√y = 1
√x = 3
y = 9
(iii) 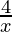 + 3年= 14
+ 3年= 14
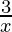 – 4y = 23
– 4y = 23
解决方案:
Lets, take 1/x = a
Here, the two given equation will be as follows:
4a + 3y = 14 -(1)
and,
3a – 4y = 23 -(2)
Now, by using Elimination method,
Multiply eq(1) by 3 and multiply eq(2) by 4, and then subtract them

-25y = 50
y = -2
Now putting y = -2 in eq(1), we get
4a + 3(-2) = 14
4a = 20
a = 5
So, Now As
a = 1/x = 5
x = 1/5
y = -2
(iv) 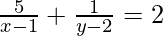
解决方案:
Lets, take ![]() = a and,
= a and, ![]() = b
= b
Here, the two given equation will be as follows:
5a + b = 2 -(1)
and,
6a – 3b = 1 -(2)
Now, by using Elimination method,
Multiply eq(1) by 3, and then add them

21a = 7
a = 1/3
Now putting a = 1/3 in eq(1), we get
5(1/3) + b = 2
b = 2 – 5/3
b = 1/3
So, Now As
a = ![]()
x – 1 = 3
x = 4
b = ![]()
y – 2 = 3
y = 5
(v) 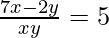
解决方案:
![]() = 5
= 5
![]() = 15
= 15
Lets, take 1/x = a and 1/y = b
Here, the two given equation will be as follows:
7b – 2a = 5 -(1)
and,
8b + 7a = 15 -(2)
Now, by using Elimination method,
Multiply eq(1) by 7, multiply eq(2) by 2 and then add them

65b = 65
b = 1
Now putting b = 1 in eq(1), we get
7(1) – 2a = 5
2a = 7 – 5
a = 1
So, Now As
a = 1/x = 1
x = 1
b = 1/y = 1
y = 1
(vi)6x + 3y = 6xy
2x + 4y = 5xy
解决方案:
Divide both the equations by xy, we get
![]() = 6
= 6
![]() = 5
= 5
Lets, take 1/x = a and, 1/y = b
Here, the two given equation will be as follows:
6b + 3a = 6
Divide the above equation by 2,
2b + a = 2 -(1)
and,
2b + 4a = 5 -(2)
Now, by using Elimination method,
Subtract eq(1) from eq(2), we get

3a = 3
a = 1
Now putting a = 1 in eq(1), we get
2b + 1 = 2
b = 1/2
So, Now As
a = 1/x = 1
x = 1
b = 1/y = 1/2
y = 2
(vii) 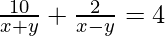
解决方案:
Lets, take ![]() = a and
= a and ![]() = b
= b
Here, the two given equation will be as follows:
10a + 2b = 4
Divide the above equation by 2,
5a + b = 2 -(1)
and,
15a – 5b = -2 -(2)
Now, by using Elimination method,
Multiply eq(1) by 3 and subtract them,

8b = 8
b = 1
Now putting b = 1 in eq(1), we get
5a + 1 = 2
a = 1/5
So, Now As
a = ![]() =
= ![]()
x + y = 5 -(3)
b = ![]() = 1
= 1
x – y = 1 -(4)
By adding eq(3) and (4), we get
2x = 6
x = 3 and y = 2
(viii) 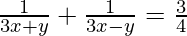
解决方案:
Lets, take ![]() = a
= a
and, ![]() = b
= b
Here, the two given equation will be as follows:
a + b = 3/4 -(1)
and,
![]()
Multiply it by 2, we get
a – b = -1/4 -(2)
Now, by using Elimination method,
Add eq(1) and eq(1), we get

2a = 1/2
a = 1/4
Now putting a = 1/4 in eq(1), we get
![]() + b =
+ b = ![]()
b = 1/2
So, Now As
a =![]()
3x + y = 4 -(3)
b = ![]()
3x – y = 2 -(4)
By adding eq(3) and eq(4), we get
6x = 6
x = 1 and y = 1
问题2.将以下问题表达为一对方程,从而找到它们的解决方案:
(i)Ritu可以在2小时内向下游划20公里,在2小时内向上游划4公里。找到她在静水中划船的速度和水流的速度。
解决方案:
Let us consider,
Speed of Ritu in still water = x km/hr
Speed of Stream = y km/hr
Now, speed of Ritu during,
Downstream = (x + y) km/h
Upstream = (x – y) km/h
As Speed = ![]()
According to the given question,
x + y = 20/2
x + y = 10 -(1)
and,
x – y = 4/2
x – y = 2 -(2)
Add eq(1) and eq(2), we get
2x = 12
x = 6 and y = 4
Hence, speed of Ritu rowing in still water = 6 km/hr
Speed of Stream = 4 km/hr
(ii)2名女性和5名男性可以在4天内一起完成刺绣工作,而3名女性和6名男性可以在3天内完成刺绣工作。找出一位女性独自完成工作所花费的时间,以及一位男性独自所花费的时间。
解决方案:
Let’s take,
The total number of days taken by women to finish the work = x
The total number of days taken by men to finish the work = y
Work done by women in one day will be = 1/x
Work done by women in one day will be = 1/y
So, according to the question
4(![]() ) = 1
) = 1
And, 3(![]() ) = 1
) = 1
Lets, take 1/x = a and, 1/y = b
Here, the two given equation will be as follows:
4(2a + 5b) = 1
8a + 20b = 1 -(1)
and,
3(3a + 6b) = 1
9a + 18b = 1 -(2)
Now, by using Cross multiplication method,
![]()
![]()
a = ![]()
b = 1/36
So, Now As
a =![]()
x = 18
b = ![]()
y = 36
Hence, number of days taken by women to finish the work = 18 days
Number of days taken by men to finish the work = 36 days.
(iii)鲁希(Roohi)部分地乘火车和部分巴士前往她家300公里。如果乘火车旅行60公里,然后乘公共汽车旅行,则需要4个小时。如果她乘火车旅行100公里,其余乘公共汽车旅行,则需要花费10分钟以上的时间。分别找到火车和公共汽车的速度。
解决方案:
Lets, take
Speed of the train = x km/h
Speed of the bus = y km/h
According to the given question,
![]() = 4
= 4
![]()
Lets, take 1/x = a and 1/y = b
Here, the two given equation will be as follows:
60a + 240b = 4
Divide it by 4, we get
15a + 60b = 1 -(1)
and,
100a + 200b = 25/6
Divide it by 25/6, we get
24a + 48b = 1 -(2)
Now, by using Cross multiplication method,
![]()
![]()
a = ![]() =
= ![]()
b = ![]() =
= ![]()
So, Now As
a = ![]() =
= ![]()
x = 60
b = ![]() =
= ![]()
y = 80
Hence, speed of the train = 60 km/h
Speed of the bus = 80 km/h