在本章中，我们将了解Z变换的基本属性。

线性度

它指出，当两个或多个单独的离散信号乘以常数时，它们各自的Z变换也将乘以相同的常数。

数学上

$$ a_1x_1(n)+ a_2x_2(n)= a_1X_1(z)+ a_2X_2(z)$$

证明-我们知道，

$$ X(Z)= \ sum_ {n =-\ infty} ^ \ infty x(n)Z ^ {-n} $$

$ = \ sum_ {n =-\ infty} ^ \ infty(a_1x_1(n)+ a_2x_2(n))Z ^ {-n} $

$ = a_1 \ sum_ {n =-\ infty} ^ \ infty x_1(n)Z ^ {-n} + a_2 \ sum_ {n =-\ infty} ^ \ infty x_2(n)Z ^ {-n} $

$ = a_1X_1(z)+ a_2X_2(z)$ (已证明)

在这里，ROC是$ ROC_1 \ bigcap ROC_2 $。

时移

时移特性描述了离散信号中时域的变化将如何影响Z域，可将其写为：

$$ x(n-n_0)\ longleftrightarrow X(Z)Z ^ {-n} $$

或$ x(n-1)\ longleftrightarrow Z ^ {-1} X(Z)$

证明–

设$ y(P)= X(PK)$

$ Y(z)= \ sum_ {p =-\ infty} ^ \ infty y(p)Z ^ {-p} $

$ = \ sum_ {p =-\ infty} ^ \ infty(x(pk))Z ^ {-p} $

令s = pk

$ = \ sum_ {s =-\ infty} ^ \ infty x(s)Z ^ {-(s + k)} $

$ = \ sum_ {s =-\ infty} ^ \ infty x(s)Z ^ {-s} Z ^ {-k} $

$ = Z ^ {-k} [\ sum_ {s =-\ infty} ^ \ infty x(m)Z ^ {-s}] $

$ = Z ^ {-k} X(Z)$ (因此证明)

在这里，ROC可以写为Z = 0(p> 0)或Z =∞(p <0)

例

U(n)和U(n-1)可以绘制如下

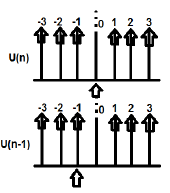
U(n)的Z变换可写为：

$ \ sum_ {n =-\ infty} ^ \ infty [U(n)] Z ^ {-n} = 1 $

U(n-1)的Z变换可以写为：

$ \ sum_ {n =-\ infty} ^ \ infty [U(n-1)] Z ^ {-n} = Z ^ {-1} $

因此，这里$ x(n-n_0)= Z ^ {-n_0} X(Z)$ (因此证明)

时间缩放

Time Scaling属性告诉我们，当时间以离散形式缩放时，信号的Z域将是什么?

$$ a ^ nx(n)\ longleftrightarrow X(a ^ {-1} Z)$$

证明–

设$ y(p)= a ^ {p} x(p)$

$ Y(P)= \ sum_ {p =-\ infty} ^ \ infty y(p)Z ^ {-p} $

$ = \ sum_ {p =-\ infty} ^ \ infty a ^ px(p)Z ^ {-p} $

$ = \ sum_ {p =-\ infty} ^ \ infty x(p)[a ^ {-1} Z] ^ {-p} $

$ = X(a ^ {-1} Z)$ (因此证明)

ROC：= Mod(ar1)

例

让我们使用时间缩放属性确定$ x(n)= a ^ n \ cos \ omega n $的Z变换。

解决方案–

我们已经知道信号$ \ cos(\ omega n)$的Z变换由-

$$ \ sum_ {n =-\ infty} ^ \ infty(\ cos \ omega n)Z ^ {-n} =(Z ^ 2-Z \ cos \ omega)/(Z ^ 2-2Z \ cos \ omega +1)$$

现在，应用时间缩放属性，可以将$ a ^ n \ cos \ omega n $的Z转换写为：

$ \ sum_ {n =-\ infty} ^ \ infty(a ^ n \ cos \ omega n)Z ^ {-n} = X(a ^ {-1} Z)$

$ = [(a ^ {-1} Z)^ 2-(a ^ {-1} Z \ cos \ omega n)] /(((a ^ {-1} Z)^ 2-2(a ^ {- 1} Z \ cos \ omega n)+1)$

$ = Z(Za \ cos \ omega)/(Z ^ 2-2az \ cos \ omega + a ^ 2)$

连续分化

连续微分特性表明，当我们在时域上相对于时间微分离散信号时，将发生Z变换。如下所示。

$$ \ frac {dx(n)} {dn} =(1-Z ^ {-1})X(Z)$$

证明–

考虑等式的LHS- $ \ frac {dx(n)} {dn} $

$$ = \ frac {[x(n)-x(n-1)]} {[n-(n-1)]} $$

$ = x(n)-X(n-1)$

$ = x(Z)-Z ^ {-1} x(Z)$

$ =(1-Z ^ {-1})x(Z)$ (因此证明)

ROC：R1

例

让我们找到由$ x(n)= n ^ 2u(n)$给出的信号的Z变换

通过属性我们可以写

$ Zz [nU(n)] = -Z \ frac {dZ [U(n)]} {dz} $

$ = -Z \ frac {d [\ frac {Z} {Z-1}]} {dZ} $

$ = Z /((Z-1)^ 2 $

$ = y(let)$

现在，再次应用该属性即可找到Z [ny]，

$ Z(n，y)= -Z \ frac {dy} {dz} $

$ = -Z \ frac {d [Z /(Z-1)^ 3]} {dz} $

$ = Z(Z + 1)/(Z-1)^ 2 $

卷积

这描绘了当卷积以离散信号形式发生时系统Z域的变化，可以写成-

$ x_1(n)* x_2(n)\ longleftrightarrow X_1(Z).X_2(Z)$

证明–

$ X(Z)= \ sum_ {n =-\ infty} ^ \ infty x(n)Z ^ {-n} $

$ = \ sum_ {n =-\ infty} ^ \ infty [\ sum_ {k =-\ infty} ^ \ infty x_1(k)x_2(nk)] Z ^ {-n} $

$ = \ sum_ {k =-\ infty} ^ \ infty x_1(k)[\ sum_n ^ \ infty x_2(nk)Z ^ {-n}] $

$ = \ sum_ {k =-\ infty} ^ \ infty x_1(k)[\ sum_ {n =-\ infty} ^ \ infty x_2(nk)Z ^ {-(nk)} Z ^ {-k}] $

令nk = l，则上式可写为-

$ X(Z)= \ sum_ {k =-\ infty} ^ \ infty x_1(k)[Z ^ {-k} \ sum_ {l =-\ infty} ^ \ infty x_2(l)Z ^ {-l }] $

$ = \ sum_ {k =-\ infty} ^ \ infty x_1(k)X_2(Z)Z ^ {-k} $

$ = X_2(Z)\ sum_ {k =-\ infty} ^ \ infty x_1(Z)Z ^ {-k} $

$ = X_1(Z).X_2(Z)$ (已证明)

ROC：$ ROC \ bigcap ROC2 $

例

让我们找到两个信号给定的卷积

$ x_1(n)= \ lbrace 3，-2,2 \ rbrace $ …(等式1)

$ x_2(n)= \ lbrace 2,0 \ leq 4 \ quad和\ quad 0 \ quad other \ rbrace $ …( eq.2 )

第一个方程的Z变换可以写成

$ \ sum_ {n =-\ infty} ^ \ infty x_1(n)Z ^ {-n} $

$ = 3-2Z ^ {-1} + 2Z ^ {-2} $

第二信号的Z变换可以写为：

$ \ sum_ {n =-\ infty} ^ \ infty x_2(n)Z ^ {-n} $

$ = 2 + 2Z ^ {-1} + 2Z ^ {-2} + 2Z ^ {-3} + 2Z ^ {-4} $

因此，上述两个信号的卷积由下式给出：

$ X(Z)= [x_1(Z)^ * x_2(Z)] $

$ = [3-2Z ^ {-1} + 2Z ^ {-2}] \次[2 + 2Z ^ {-1} + 2Z ^ {-2} + 2Z ^ {-3} + 2Z ^ {-4 }] $

$ = 6 + 2Z ^ {-1} + 6Z ^ {-2} + 6Z ^ {-3} + … \ quad … \ quad … $

取Z逆变换，

$ x(n)= \ lbrace 6,2,6,6,6,0,4 \ rbrace $

初值定理

如果x(n)是一个因果序列，其Z变换为X(z)，则初始值定理可以写为：

$ X(n)(at \ quad n = 0)= \ lim_ {z \ to \ infty} X(z)$

证明-我们知道，

$ X(Z)= \ sum_ {n = 0} ^ \ infty x(n)Z ^ {-n} $

扩展以上系列，我们得到：

$ = X(0)Z ^ 0 + X(1)Z ^ {-1} + X(2)Z ^ {-2} + … \ quad … $

$ = X(0)\ times 1 + X(1)Z ^ {-1} + X(2)Z ^ {-2} + … \ quad … $

在上述情况下，如果Z→∞，则$ Z ^ {-n} \ rightarrow 0 $(因为n> 0)

因此，我们可以说；

$ \ lim_ {z \ to \ infty} X(z)= X(0)$ (因此证明)

终值定理

最终值定理指出，如果信号的Z变换表示为X(Z)且极点都在圆内，则其最终值表示为x(n)或X(∞)并可以写为-

$ X(\ infty)= \ lim_ {n \ to \ infty} X(n)= \ lim_ {z \ to 1} [X(Z)(1-Z ^ {-1})] $

条件–

• 它仅适用于因果系统。
• $ X(Z)(1-Z ^ {-1})$应该在Z平面的单位圆内具有极点。

证明-我们知道

$ Z ^ + [x(n + 1)-x(n)] = \ lim_ {k \ to \ infty} \ sum_ {n = 0} ^ kZ ^ {-n} [x(n + 1)-x (n)] $

$ \ Rightarrow Z ^ + [x(n + 1)]-Z ^ + [x(n)] = \ lim_ {k \ to \ infty} \ sum_ {n = 0} ^ kZ ^ {-n} [x (n + 1)-x(n)] $

$ \ Rightarrow Z [X(Z)^ +-x(0)]-X(Z)^ + = \ lim_ {k \ to \ infty} \ sum_ {n = 0} ^ kZ ^ {-n} [x (n + 1)-x(n)] $

在这里，我们可以应用单面Z变换的高级属性。因此，以上等式可以重写为：

$ Z ^ + [x(n + 1)] = Z [X(2)^ +-x(0)Z ^ 0] = Z [X(Z)^ +-x(0)] $

现在将z = 1放在上面的公式中，我们可以展开上面的公式-

$ \ lim_ {k \ to \ infty} {[x(1)-x(0)+ x(6)-x(1)+ x(3)-x(2)+ … \ quad … \ quad … + x(x + 1)-x(k)]} $

这可以表述为：

$ X(\ infty)= \ lim_ {n \ to \ infty} X(n)= \ lim_ {z \ to 1} [X(Z)(1-Z ^ {-1})] $ (已证明)

例

让我们找到x(n)的初始值和最终值，其信号由

$ X(Z)= 2 + 3Z ^ {-1} + 4Z ^ {-2} $

解决方案-首先让我们通过应用定理找到信号的初始值

$ x(0)= \ lim_ {z \ to \ infty} X(Z)$

$ = \ lim_ {z \ to \ infty} [2 + 3Z ^ {-1} + 4Z ^ {-2}] $

$ = 2 +(\ frac {3} {\ infty})+(\ frac {4} {\ infty})= 2 $

现在让我们根据定理找到信号的最终值

$ x(\ infty)= \ lim_ {z \ to \ infty} [(1-Z ^ {-1})X(Z)] $

$ = \ lim_ {z \ to \ infty} [(1-Z ^ {-1})(2 + 3Z ^ {-1} + 4Z ^ {-2})] $

$ = \ lim_ {z \ to \ infty} [2 + Z ^ {-1} + Z ^ {-2} -4Z ^ {-3}] $

$ = 2 + 1 + 1-4 = 0 $

Z变换的其他一些属性在下面列出–

频率差异

当其离散信号随时间变化时，它会给出信号Z域的变化。

$ nx(n)\ longleftrightarrow -Z \ frac {dX(z)} {dz} $

它的ROC可以写为：

$ r_2

例

让我们通过频率微分找到x(n)的值，其Z域中的离散信号由$ x(n)\ longleftrightarrow X(Z)= log(1 + aZ ^ {-1})$给出

通过属性，我们可以这样写

$ nx(n)\ longleftrightarrow -Z \ frac {dx(Z)} {dz} $

$ = -Z [\ frac {-aZ ^ {-2}} {1 + aZ ^ {-1}}] $

$ =(aZ ^ {-1})/(1 + aZ ^ {-1})$

$ = 1-1 /(1 + aZ ^ {-1})$

$ nx(n)= \ delta(n)-(-a)^ nu(n)$

$ \ Rightarrow x(n)= 1 / n [\ delta(n)-(-a)^ nu(n)] $

时间倍增

当在离散信号电平上进行乘法运算时，它会给出信号Z域的变化。

$ x_1(n).x_2(n)\ longleftrightarrow(\ frac {1} {2 \ Pi j})[X1(Z)* X2(Z)] $

时间共轭

这描绘了Z域中共轭离散信号的表示。

$ X ^ *(n)\ longleftrightarrow X ^ *(Z ^ *)$