第 11 类 NCERT 解决方案 - 第 2 章关系和函数 - 第 2 章的杂项练习

问题 1.关系 f 定义为 f(x) = {x ² , 0 ≤ x ≤ 3 3x, 3 ≤ x ≤ 10}

关系 g 由 g(x) = {x ² , 0 ≤ x ≤ 2 3x, 2 ≤ x ≤ 10} 定义。

证明 f 是一个函数，而 g 不是一个函数。

解决方案：

The given relation f is defined as:

f(x) = {x², 0≤x≤3

            3x, 3≤x≤10}

It is given that, for the condition 0 ≤ x < 3,

Solution of f(x) = x² and  

For the condition 3 < x ≤ 10, solution of f(x) = 3x.

Now for the value of x = 3, solution of f(x) by putting the value of x, f(x) = 3² = 9 

or, f(x) = 3 × 3 = 9.

That means, at x = 3, f(x) = 9 [Single image]

So that, for 0 ≤ x ≤ 10, the images of f(x) are unique.

Therefore, the given relation is a function.

Now,

In the given relation g is defined as:

g(x) = {x², 0≤x≤2

                3x, 2≤x≤10}

It is seen that, in case of both the condition, for x = 2,

The value of g(x), by putting the value of x, g(x) = 2²= 4 and g(x) = 3 × 2 = 6.

So that, element 2 of the domain of the relation g corresponds to two different images i.e., 4 and 6.

Therefore, this relation is not a function.

问题 2. 如果 f(x) = x ² ，求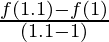$\tfrac{f(1.1) - f(1)}{(1.1 - 1)}$ .

解决方案：

Given:

f(x) = x² .

Hence, by putting the condition of f(x) in f(1.1) and f(1), 

we can find the result of the given equation

((f(1.1) – f(1))/(1.1 – 1)) = (((1.1)²  – (1)²)/(1.1 – 1)) 

                                  = ((1.21-1)/(0.1))

                                  = (0.21/0.1) 

                                  = 2.1 

问题 3. 求函数f(x) = 的域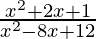$\tfrac{x^2+2x+1}{x^2-8x+12}$ ((x ² +2x+1)/(x ² -8x+12))。

解决方案：

Given function:

f(x) = ((x²+2x+1)/(x²-8x+12))

      = (((x²+2x+1)/((x-6)(x-2)))

It is clearly notified that, the function f is defined for all real numbers except 

at x = 6 and x = 2 as the denominator becomes zero otherwise.

问题 4. 找到由 f(x) = √(x – 1) 定义的实函数f 的域和范围。

解决方案：

Given real function:

f(x) = √(x – 1).

Clearly it is notified, √(x – 1) is defined for (x – 1) ≥ 0.

Hence, the function f(x) = √(x – 1) is defined for x ≥ 1.

So that, the domain of f is the set of all real numbers greater than or equal to 1.

 Domain of f = [1, ∞).

Now,

According to the condition, x ≥ 1 ⇒ (x – 1) ≥ 0 ⇒ √(x – 1) ≥ 0

That’s why, the range of f is the set of all real numbers greater than or equal to 0.

Range of f = [0, ∞).

Therefore, the domain of f is R – {2, 6}.

问题 5. 找到由 f (x) = |x – 1| 定义的实函数f 的域和范围。

解决方案：

Given real function: f(x) = |x – 1|

Clearly it is notified that, the function |x – 1| is defined for all real numbers.

Hence, Domain of f = R

Also, according to the condition , for x ∈ R, |x – 1| assumes all real numbers.

So that, the range of f is the set of all non-negative real numbers.

问题 6. 令 f={(x, 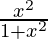$\tfrac{x^2}{1+x^2}$ )}: x ∈ R} 是一个从 R 到 R 的函数。确定 f 的范围。

解决方案：

Given function:

f = {(x, x²/1+x²): x ∈ R}

Substituting values and determining the images, we have

={(0,0), (±0.5, 1/5), (±1, 1/2), (±1.5, 9/13), (±2, 4/5), (3, 9/10), (4,16/17), …..}

From the above equation, the range of f is the set of all second elements.

 It can be notified that all these elements are greater than or equal to 0 but less than 1.

[As the denominator is greater than the numerator.]

Or, We know that, for x ∈ R,

x²≥ 0

Then,

x² + 1 ≥ x²

1 ≥ (x² / (x² + 1))

Therefore, the range of f = [0, 1)

问题 7. 设 f, g: R → R 分别定义为 f(x) = x + 1, g(x) = 2x – 3. 求 f + g, f – g, 和 f/g。

解决方案：

According to the question, let us assume, the functions f, g: R → R is defined as

given conditions f(x) = x + 1, g(x) = 2x – 3.

Now,

We find that (f + g) (x) = f(x) + g(x) = (x + 1) + (2x – 3) = 3x – 2

So that, (f + g) (x) = 3x – 2

Now, we find that, (f – g) (x) = f(x) – g(x) = (x + 1) – (2x – 3) = x + 1 – 2x + 3 = – x + 4

So that, (f – g) (x) = -x + 4

(f/g(x)) = f(x)/g(x), g(x) ≠ 0, x ∈ R

(f/g(x)) = x + 1/ 2x – 3, 2x – 3 ≠ 0

So that, (f/g(x)) = x + 1/ 2x – 3, x ≠ 3/2.

问题 8. 令 f = {(1, 1), (2, 3), (0, –1), (–1, –3)} 为由 f(x) = ax + 定义的从 Z 到 Z 的函数b，对于一些整数a，b。确定a，b。

解决方案：

Given the values, f = {(1, 1), (2, 3), (0, –1), (–1, –3)}

And according to the question, the function is defined as, f(x) = ax + b

For (1, 1) ∈ f

We have, f(1) = 1

So, a × 1 + b = 1

a + b = 1 …. (i)

And for (0, -1) ∈ f

We have f(0) = -1

a × 0 + b = -1

So, b = -1

Now, On substituting b = –1 in (i), we get

Putting the value here, a + (–1) = 1 ⇒ a = 1 + 1 = 2.

Hereby, the values of a and b are 2 and –1 respectively.

问题 9. 设 R 是由 R = {(a, b): a, b ∈ N and a = b2} 定义的从 N 到 N 的关系。以下是真的吗？

(i) (a, a) ∈ R, 对于所有 a ∈ N

(ii) (a, b) ∈ R, 蕴含 (b, a) ∈ R

(iii) (a, b) ∈ R, (b, c) ∈ R 蕴含 (a, c) ∈ R。

在每种情况下证明你的答案。

解决方案：

According to the question, Given relation R = {(a, b): a, b ∈ N and a = b2}

(i) It can be notified that 2 ∈ N; however, 2 ≠ 22 = 4.

Hence, it is notified that the statement “(a, a) ∈ R, for all a ∈ N” is not true.

(ii) Its clearly notified that (9, 3) ∈ N because 9, 3 ∈ N and 9 = 32.

Now, it’s clear that 3 ≠ 92 = 81; therefore, (3, 9) ∉ N

Hence, it is notified that the statement “(a, b) ∈ R, implies (b, a) ∈ R” is not true.

(iii) Its clearly notified that (16, 4) ∈ R, (4, 2) ∈ R because 16, 4, 2 ∈ N and 16 = 42 and 4 = 22.

Now, it is clear that 16 ≠ 22 = 4; therefore, (16, 2) ∉ N

Hence, it is notified that the statement “(a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R” is not true.

问题 10. 设 A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} 和 f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}。以下是真的吗？

(i) f 是从 A 到 B 的关系

(ii) f 是从 A 到 B 的函数。

在每种情况下证明你的答案。

解决方案：

Given, A = {1, 2, 3, 4} and B = {1, 5, 9, 11, 15, 16}

So,

A × B = {(1, 1), (1, 5), (1, 9), (1, 11), (1, 15), (1, 16), (2, 1), (2, 5),

               (2, 9), (2, 11), (2, 15), (2, 16), (3, 1), (3, 5), (3, 9), (3, 11),

               (3, 15), (3, 16), (4, 1), (4, 5), (4, 9), (4, 11), (4, 15), (4, 16)}

Also given in the question that, f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}

(i) The verified statement is : A relation from a non-empty set A to a non-empty 

set B is a subset of the Cartesian product A × B.

It’s clearly notified that f is a subset of A × B.

Hence, it’s clear that f is a relation from A to B.

(ii) From the given condition, as the same first element i.e., 2 corresponds to two 

different images (9 and 11), relation f is not a function.

问题 11. 设 f 是由 f = {(ab, a + b): a, b ∈ Z} 定义的 Z × Z 的子集。从 Z 到 Z 的 fa函数：证明你的答案是正确的吗？

解决方案：

According to the question, Given relation f is defined as f = {(ab, a + b): a, b ∈ Z}.

Now, we know that a relation f from a set A to a set B is said to be a function 

if every element of set A has unique images in set B.

As 2, 6, –2, –6 ∈ Z, (2 × 6, 2 + 6), (–2 × –6, –2 + (–6)) ∈ f

i.e., (12, 8), (12, –8) ∈ f

It’s clearly notified that, the same first element, 12 corresponds 

to two different images (8 and –8).

Therefore, the relation f is not a function.

问题 12. 令 A = {9, 10, 11, 12, 13} 并让 f: A → N 定义为 f(n) = n 的最高质因子。求 f 的范围。

解决方案：

Given, A = {9, 10, 11, 12, 13}

Now, f: A → N is defined as

f(n) = The highest prime factor of n.

So, Prime factor of 9 = 3

Prime factors of 10 = 2, 5

Prime factor of 11 = 11

Prime factors of 12 = 2, 3

Prime factor of 13 = 13

Hence, it can be expressed as:

Here, 

f(9) means the highest prime factor of 9 = 3

f(10) means the highest prime factor of 10 = 5

f(11) means the highest prime factor of 11 = 11

f(12) means the highest prime factor of 12 = 3

f(13) means the highest prime factor of 13 = 13

So that, the range of f is the set of all f(n), where n ∈ A.

Therefore,

Range of f = {3, 5, 11, 13}.